НОУ ИНТУИТ | Введение в алгебру. Лекция 4: Кольцо многочленов от одной переменной

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Определение 1.13.22. Пусть $f(x),g(x)\in K[x]$ . Многочлен $d(x)\in K[x]$ называется наибольшим общим делителем (НОД) многочленов f(x) и g(x), если:

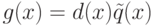d(x) - общий делитель многочленов f(x) и g(x) (т. е. f(x)=d(x)q(x), $g(x)=d(x)\tilde q(x)$ );
для любого общего делителя d'(x) многочленов f(x) и g(x) многочлен d(x) делится на d'(x).

Обозначение: 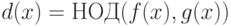$d(x)=\NOD(f(x),g(x))$ .

Замечание 1.13.23. Из 2) следует, что deg d(x) >= deg d'(x), т. е. что 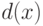d(x) - общий делитель наибольшей степени. Правда, нам еще надо установить существование $\NOD$ в нашем смысле.

Теорема 1.13.24 (алгоритм Евклида). Для любых $f(x),g(x)\in K[x]$ :

существует наибольший общий делитель d(x) многочленов f(x) и g(x) ;
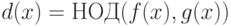$d(x)=\NOD(f(x),g(x))$ находится по процедуре последовательного деления,восходящей к Евклиду;
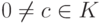наибольший делитель d(x) определен однозначно с точностью до ненулевой константы $0\ne c\in K$ .

Доказательство. 1), 2) Рассмотрим процедуру Евклида:

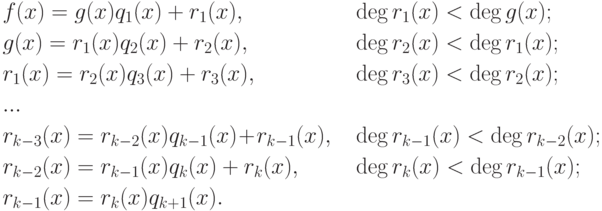
$\begin{alignat*}{2} & f(x)=g(x)q_1(x)+r_1(x), && \deg r_1(x)<\deg g(x);\\ & g(x)=r_1(x)q_2(x)+r_2(x), && \deg r_2(x)<\deg r_1(x);\\ & r_1(x)=r_2(x)q_3(x)+r_3(x), && \deg r_3(x)<\deg r_2(x);\\ &...\\ & r_{k-3}(x)=r_{k-2}(x)q_{k-1}(x)\!+\! r_{k-1}(x), &\quad &\deg r_{k-1}(x)<\deg r_{k-2}(x);\\ & r_{k-2}(x)=r_{k-1}(x)q_k(x)+r_k(x), && \deg r_k(x)<\deg r_{k-1}(x);\\ & r_{k-1}(x)=r_k(x)q_{k+1}(x). \end{alignat*}$

а) Поднимаясь последовательно вверх, мы видим, что r_k(x) - общий делитель многочленов g(x) и f(x).

б) Если d'(x) - общий делитель многочленов f(x) и g(x), то, опускаясь последовательно вниз, мы видим, что d'(x) - делитель многочлена d(x).

3) Если d(x) и d'(x) - два наибольших общих делителя, то они делятся друг на друга, и поэтому d'(x)=cd(x), 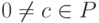$0\ne c\in P$ . Ясно, что если d(x) - наибольший общий делитель и 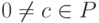$0\ne c\in P$ , то cd(x) - также наибольший общий делитель.

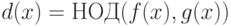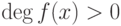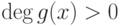Теорема 1.13.25 (о выражении наибольшего общего делителя через исходные многочлены). Если $f(x),g(x)\in K[x]$ и $d(x)=\NOD(f(x),g(x))$ , то существуют многочлены $u(x),v(x)\in K[x]$ такие, что d(x)=f(x)u(x)+g(x)v(x) (если при этом $\deg f(x)>0$ , $\deg g(x)>0$ , то можно считать, что

$\begin{align*} \deg u(x)&<\deg g(x),\\ \deg v(x)&<\deg f(x); \end{align*}$

это позволяет искать многочлены u(x), v(x) с неопределенными коэффициентами).

Доказательство. Существование таких многочленов u(x), v(x) следует из алгоритма Евклида нахождения d(x)=r_k(x). Мы выражаем последовательно r_k(x) сначала через r_k-2(x) и r_k-1(x), потом, подставляя выражение r_k-1(x) через r_k-3(x) и r_k-2(x), через r_k-3(x) и r_k-2(x) и, завершая подъем, через g(x) и f(x).

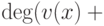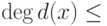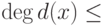Если найдены "плохие" u(x) и v(x), пусть, например, $\deg u(x)\pgeq \deg g(x)$ , то u(x)=g(x)q(x)+r(x), и поэтому d(x)=f(x)r(x)+g(x)[v(x)+f(x)q(x)]. Из сравнения степеней следует, что $\deg(v(x)\+f(x)q(x))\!<\!\deg f(x)$ , поскольку $\deg(f(x)r(x))\!<\!\deg f(x)\!+\!\deg g(x)$ , $\deg d(x)\pleq\deg f(x)$ , $\deg d(x)\pleq\deg g(x)$ .

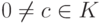Определение 1.13.26. Многочлены $f(x),g(x)\in K[x]$ из кольца многочленов K[x] над полем K называются взаимно простыми, если их наибольший делитель d(x) равен 1 (т. е. их общие делители - это лишь ненулевые многочлены нулевой степени $0\ne c\in K$ ).

Теорема 1.13.27. Многочлены $f(x),g(x)\in K[x]$ взаимно просты тогда и только тогда, когда существуют такие многочлены $u(x),v(x)\in K[x]$ , что f(x)u(x)+g(x)v(x)=1.

Доказательство.

Если многочлены f(x) и g(x) взаимно просты, то для их наибольшего делителя d(x) имеем равенство d(x)=1. Принимая во внимание выражение многочлена d(x) через f(x) и g(x), получаем, что для некоторых $u(x),v(x)\in K[x]$ f(x)u(x)+g(x)v(x)=1.
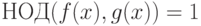Если для $u(x),v(x)\in K[x]$ имеем f(x)u(x)+g(x)v(x)=1, то любой общий делитель многочленов f(x) и g(x) является делителем многочлена 1. Таким образом, $\NOD(f(x),g(x))=1$ , другими словами, многочлены f(x) и g(x) взаимно просты.

Замечание 1.13.28. Многочлены f(x) и g(x) взаимно просты тогда и только тогда, когда K[x]f(x)+K[x]g(x)=K[x] (идеал кольца K[x], порожденный многочленами f(x) и g(x), совпадает со всем кольцом многочленов K[x] ).

Теорема 1.13.29 (основные свойства взаимно простых многочленов). Пусть $f(x),g(x),\varphi(x),\psi(x)\in K[x]$ .

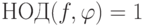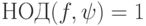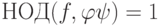Если $\NOD(f,\varphi)=1$ , $\NOD(f,\psi)=1$ , то $\NOD(f,\varphi\psi)=1$ .
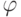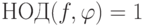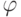Если fg делится на $\varphi$ и $\NOD(f,\varphi)=1$ , то g делится на $\varphi$ .
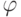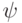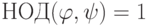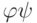Если f делится на $\varphi$ и делится на $\psi$ , $\NOD(\varphi,\psi)=1$ , то f делится на $\varphi\psi$ .

Доказательство.

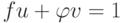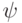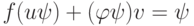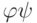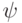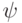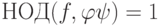1) Пусть $fu+\varphi v=1$ для $u(x),v(x)\in K[x]$ . Умножая это равенство на $\psi$ , получаем $f(u\psi)+(\varphi\psi)v=\psi$ . Отсюда следует, что любой общий делитель многочленов f и $\varphi\psi$ является делителем многочлена $\psi$ , но многочлены f и $\psi$ взаимно просты. Таким образом, $\NOD(f,\varphi\psi)=1$ .
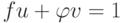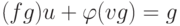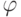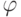2) Пусть для $u(x),v(x)\in K[x]$ имеем $fu+\varphi v=1$ . Умножив это равенство на g(x), получим $(fg)u+\varphi(vg)=g$ , и поэтому многочлен g делится на $\varphi$ , поскольку оба слагаемых в левой части делятся на $\varphi$ .
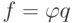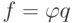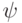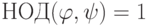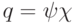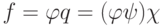
3) Пусть $f=\varphi q$ , где $q(x)\in K[x]$ . Так как $f=\varphi q$ делится на $\psi$ и $\NOD(\varphi,\psi)=1$ , то, в силу 2), $q=\psi\chi$ , где $\chi(x)\in K[x]$ . Итак: $f=\varphi q=(\varphi\psi)\chi$

Замечание 1.13.30. Определив наибольший общий делитель 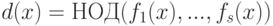$d(x)=\NOD(f_1(x),...,f_s(x))$ многочленов $f_1(x),...,f_s(x)\in K[x],\quad s \geq 1$ , как такой делитель этих многочленов f₁(x),...,f_s(x), который делится на любой их общий делитель, получаем, проводя индукцию по s, что $d(x)=\NOD(f_s(x),\NOD(f_1(x),...,f_{s-1}(x)))$ .

Упражнение 1.13.31. Если $f(x)=x(x-1),\ g(x)=x(x-2),\ h(x)=(x-1)(x-2) \in R[x]$ , то $\begin{ga} \NOD(f,g)=x,\quad \NOD(f,h)=x-1,\\ \NOD(g,h)=x-2,\quad \NOD(f,g,h)=1. \end{ga}$

Замечание 1.13.32. В алгоритме Евклида можно для удобства делимое и делитель на каждом шаге умножать на любые ненулевые числа (при этом мы не заботимся о точном вычислении коэффициентов в частных q_i(x) ).

Пример 1.13.33. Найти 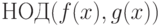$\NOD(f(x),g(x))$ , где

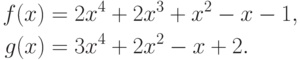
$\begin{align*} f(x) &= 2x^4+2x^3+x^2-x-1,\\ g(x) &= 3x^4+2x^2-x+2. \end{align*}$

Решение. 3f(x)=g(x)q₁(x)+r₁(x), где q₁(x)=2, r₁(x)=6x³-x²-x-7. Делим 2g(x) на r₁(x):

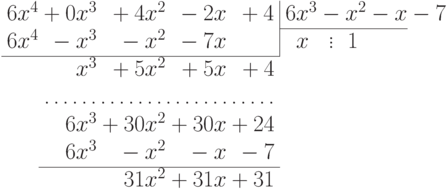
$\begin{array}{r@{}r@{}r@{}r@{}rr@{}c@{}r@{}r@{}r} 6x^4 & {}+{}0x^3 & {}+{}4x^2 & {}-{}2x & \multicolumn{1}{r|}{{}+{}4} & {}6x^3 & {}-{} & x^2 & {}-{}x & {}-{}7\\ \cline{6-9} 6x^4 & {}-{}x^3 & {}-{}x^2 & {}-{}7x & \multicolumn{1}{r|}{} & x\hphantom{{}^3} & \vdots & 1\hphantom{{}^2}\\ \cline{1-5} \rule{0pt}{15pt} & x^3 & {}+{}5x^2 & {}+{}5x & {}+{}4\\ & \multicolumn{4}{@{}c@{}}{\dotfill}\\ & 6x^3 & {}+{}30x^2 & {}+{}30x & {}+{}24\\ & 6x^3 & {}-{}x^2 & {}-{}x & {}-{}7\\ \cline{2-5} \rule{0pt}{15pt} & & 31x^2 & {}+{}31x & {}+{}31 \end{array}$

Многоточием ... отмечено место, в котором мы произвели домножение на 6 (соответственно многоточие $\vdots$ показывает, что мы не находим точные коэффициенты для q₂(x) ). Таким образом, g(x)=r₁(x)q₂(x)+r₂(x), где с точностью до ненулевого множителя r₂(x)=x²+x+1. Далее,

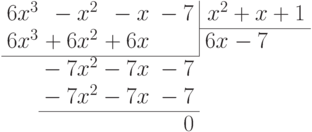
$\begin{array}{r@{}r@{}r@{}rr@{}r@{}r} 6x^3 & {}-{}x^2 & {}-{}x & \multicolumn{1}{r|}{{}-{}7} & x^2 & {}+{}x & {}+{}1\\ \cline{5-7} 6x^3 & {}+{}6x^2 & {}+{}6x & \multicolumn{1}{r|}{} & 6x & {}-{}7\\ \cline{1-4} \rule{0pt}{15pt} & {}-{}7x^2 & {}-{}7x & {}-{}7\\ & {}-{}7x^2 & {}-{}7x & {}-{}7\\ \cline{2-4} \rule{0pt}{15pt} & & & 0 \end{array}$

То есть r₁(x) делится нацело на r₂(x). Итак, 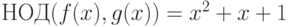$\NOD(f(x),g(x))=x^2+x+1$ .

Дальше >>

Введение в алгебру

Введение в алгебру

Кольцо многочленов от одной переменной

Вопросы и ответы

Студенты

Авторизоваться

Введение в алгебру

Введение в алгебру

Кольцо многочленов от одной переменной

Вопросы и ответы

Студенты