Основные алгоритмы и их реализация на Python
2.4 Обработка двумерных массивов (матриц)
Двумерные массивы являются аналогами матриц и имеют "прямоугольную" (табличную) структуру. Описываются массивы так же, как одномерные. Разница состоит в том, что у элемента двумерного массива две координаты (два индекса) — номер строки и номер столбца, в которых находится элемент.
Ввод массива осуществляется построчно при помощи двух циклов. Пусть  — количество столбцов,
— количество столбцов,  — количество строк. Элементы массива обозначим как mas[i, j], первый индекс — номер строки, второй — номер столбца.
— количество строк. Элементы массива обозначим как mas[i, j], первый индекс — номер строки, второй — номер столбца.
ввод M,N нц для i от 1 до N нц для j от 1 до M ввод mas[i, j] кц кц
Вывод массива на экран осуществляется при помощи аналогичных циклов.
нц для i от 1 до N нц для j от 1 до M вывод mas[i, j] кц вывод кц
Здесь "пустой" оператор вывода обеспечивает переход на новую строку.
В Python для работы с многомерными (когда используется два и более индексов) массивами можно использовать вложенные списки (списки списков, списки списков списков и т. д.).
Однако Python предоставляет более удобный инструмент создания и преобразования многомерных массивов — библиотеку numpy (Numeric Python).
Создание двумерного массива в Python может выглядеть так:
# -*- coding: utf-8 -*-
#
import numpy
n=input('Количество строк: ')
m=input('Количество столбцов: ')
# Создаём "нулевую" матрицу
a=numpy.zeros([n-1,m-1])
# Заполняем матрицу
for i in range(n-1) :
for j in range(m-1) :
print'Элемент матрицы[',i,'][',j,']'
a[i, j]=input('Введите элемент: ')
#
Сначала с помощью функции (метода) numpy.zeros() создаётся двумерный массив (матрица), заполненный нулями, а потом вместо нулей подставляются реальные значения. Индексы элементов, так же как в строках, кортежах и списках, начинаются с 0 (первый — верхний левый — элемент матрицы в Python имеет индекс [0,0]). Оператор print выводит индексы очередного элемента матрицы, который нужно ввести.
Задача 1. Выполнить обработку элементов прямоугольной матрицы  , имеющей
, имеющей  строк и
строк и  столбцов. Найти среднее арифметическое элементов массива.
столбцов. Найти среднее арифметическое элементов массива.
Постановка задачи:
Дано:
-
 — количество строк в массиве;
— количество строк в массиве; -
 — количество столбцов в массиве;
— количество столбцов в массиве; -
![A[i,j]](/sites/default/files/tex_cache/24edb2ea71428b08548c56890a88df9b.png) — элемент массива;
— элемент массива; -
 — индексы элемента массива.
— индексы элемента массива.
Найти:
-
 — сумма элементов массива (сумма всех
— сумма элементов массива (сумма всех ![A[i,j]](/sites/default/files/tex_cache/24edb2ea71428b08548c56890a88df9b.png) при всех
при всех  и
и  )
) -
 — количество элементов в массиве (
— количество элементов в массиве ( )
) -
 — среднее арифметическое элементов массива (
— среднее арифметическое элементов массива (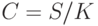 )
)
Блок-схема алгоритма решения показана на рис. 2.15.
Текст программы на "псевдоязыке":
ввод n,m S=0 нц для i от 1 до n нц для j от 1 до m ввод A[i, j] S=S+A[i, j] кц кц K=n*m C=S/K вывод C
Текст программы на Python:
# -*- coding: utf-8 -*-
#
import numpy
n=input('Количество строк: ')
m=input('Количество столбцов: ')
S=0.0
# Создаём нулевую матрицу
a=numpy.zeros([n-1,m-1])
# Заполняем матрицу
for i in range(n-1) :
for j in range(m-1) :
print 'Элемент матрицы [',i,'][',j,']'
a[i, j]=input('Введите элемент: ')
S=S+a[i, j]
#
K=n*m
C=S/K
print 'Среднее значение по строкам:',C
2.4.1 Задачи для самостоятельного решения
- Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти наибольший элемент столбца матрицы
столбцов. Найти наибольший элемент столбца матрицы  , для которого сумма абсолютных значений элементов максимальна.
, для которого сумма абсолютных значений элементов максимальна. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти наибольшее значение среди средних значений для каждой строки матрицы.
столбцов. Найти наибольшее значение среди средних значений для каждой строки матрицы. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти наименьший элемент столбца матрицы
столбцов. Найти наименьший элемент столбца матрицы  , для которого сумма абсолютных значений элементов максимальна.
, для которого сумма абсолютных значений элементов максимальна. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти наименьшее значение среди средних значений для каждой строки матрицы.
столбцов. Найти наименьшее значение среди средних значений для каждой строки матрицы. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить средние значения по всем строкам и столбцам матрицы. Результат оформить в виде матрицы из
столбцов. Определить средние значения по всем строкам и столбцам матрицы. Результат оформить в виде матрицы из  строк и
строк и 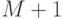 столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждого столбца. Результат оформить в виде матрицы из
столбцов. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждого столбца. Результат оформить в виде матрицы из 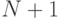 строк и
строк и  столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждой строки. Результат оформить в виде матрицы из
столбцов. Найти сумму элементов всей матрицы. Определить, какую долю в этой сумме составляет сумма элементов каждой строки. Результат оформить в виде матрицы из  строк и
строк и 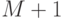 столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить, сколько отрицательных элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из
столбцов. Определить, сколько отрицательных элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из 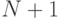 строк и
строк и 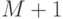 столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить, сколько нулевых элементов содержится в верхних
столбцов. Определить, сколько нулевых элементов содержится в верхних  строках матрицы и в левых
строках матрицы и в левых  столбцах матрицы.
столбцах матрицы. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Перемножить элементы каждого столбца матрицы с соответствующими элементами
столбцов. Перемножить элементы каждого столбца матрицы с соответствующими элементами  -го столбца.
-го столбца. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Просуммировать элементы каждой строки матрицы с соответствующими элементами
столбцов. Просуммировать элементы каждой строки матрицы с соответствующими элементами  -й строки.
-й строки. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Разделить элементы каждой строки на элемент этой строки с наибольшим значением.
столбцов. Разделить элементы каждой строки на элемент этой строки с наибольшим значением. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Разделить элементы каждого столбца матрицы на элемент этого столбца с наибольшим значением.
столбцов. Разделить элементы каждого столбца матрицы на элемент этого столбца с наибольшим значением. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Разделить элементы матрицы на элемент матрицы с наибольшим значением.
столбцов. Разделить элементы матрицы на элемент матрицы с наибольшим значением. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Все элементы имеют целый тип. Дано целое число
столбцов. Все элементы имеют целый тип. Дано целое число  . Определить, какие столбцы имеют хотя бы одно такое число, а какие не имеют.
. Определить, какие столбцы имеют хотя бы одно такое число, а какие не имеют. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Исключить из матрицы строку с номером
столбцов. Исключить из матрицы строку с номером  . Сомкнуть строки матрицы.
. Сомкнуть строки матрицы. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Добавить к матрице строку и вставить ее под номером
столбцов. Добавить к матрице строку и вставить ее под номером  .
. - Выполнить обработку элементов квадратной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти сумму элементов, стоящих на главной диагонали, и сумму элементов, стоящих на побочной диагонали (элементы главной диагонали имеют индексы от
столбцов. Найти сумму элементов, стоящих на главной диагонали, и сумму элементов, стоящих на побочной диагонали (элементы главной диагонали имеют индексы от ![[0,0]](/sites/default/files/tex_cache/e013e067435150802e1c67877ce69879.png) до
до ![[N,N]](/sites/default/files/tex_cache/8d7ab7ab6e387953cf52fb2317d44e04.png) , а элементы побочной диагонали – от
, а элементы побочной диагонали – от ![[N,0]](/sites/default/files/tex_cache/bd55fd0bdad535ef26f5252252852e92.png) до
до ![[0,N]](/sites/default/files/tex_cache/c06e42915defe7761a798b4211cb5a82.png) ).
). - Выполнить обработку элементов квадратной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить сумму элементов, расположенных параллельно главной диагонали (ближайшие к главной). Элементы главной диагонали имеют индексы от
столбцов. Определить сумму элементов, расположенных параллельно главной диагонали (ближайшие к главной). Элементы главной диагонали имеют индексы от ![[0,0]](/sites/default/files/tex_cache/e013e067435150802e1c67877ce69879.png) до
до ![[N,N]](/sites/default/files/tex_cache/8d7ab7ab6e387953cf52fb2317d44e04.png) .
. - Выполнить обработку элементов квадратной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить произведение элементов, расположенных параллельно побочной диагонали (ближайшие к побочной). Элементы побочной диагонали имеют индексы от
столбцов. Определить произведение элементов, расположенных параллельно побочной диагонали (ближайшие к побочной). Элементы побочной диагонали имеют индексы от ![[N,0]](/sites/default/files/tex_cache/bd55fd0bdad535ef26f5252252852e92.png) до
до ![[0,N]](/sites/default/files/tex_cache/c06e42915defe7761a798b4211cb5a82.png) .
. - Выполнить обработку элементов квадратной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Каждой паре элементов, симметричных относительно главной диагонали (ближайшие к главной), присвоить значения, равные полусумме этих симметричных значений (элементы главной диагонали имеют индексы от
столбцов. Каждой паре элементов, симметричных относительно главной диагонали (ближайшие к главной), присвоить значения, равные полусумме этих симметричных значений (элементы главной диагонали имеют индексы от ![[0,0]](/sites/default/files/tex_cache/e013e067435150802e1c67877ce69879.png) до
до ![[N,N]](/sites/default/files/tex_cache/8d7ab7ab6e387953cf52fb2317d44e04.png) ).
). - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Исходная матрица состоит из нулей и единиц. Добавить к матрице еще один столбец, каждый элемент которого делает количество единиц в каждой строке чётным.
столбцов. Исходная матрица состоит из нулей и единиц. Добавить к матрице еще один столбец, каждый элемент которого делает количество единиц в каждой строке чётным. - Выполнить обработку элементов квадратной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Найти сумму элементов, расположенных выше главной диагонали, и произведение элементов, расположенных выше побочной диагонали (элементы главной диагонали имеют индексы от
столбцов. Найти сумму элементов, расположенных выше главной диагонали, и произведение элементов, расположенных выше побочной диагонали (элементы главной диагонали имеют индексы от ![[0,0]](/sites/default/files/tex_cache/e013e067435150802e1c67877ce69879.png) до
до ![[N,N]](/sites/default/files/tex_cache/8d7ab7ab6e387953cf52fb2317d44e04.png) , а элементы побочной диагонали — от
, а элементы побочной диагонали — от ![[N,0]](/sites/default/files/tex_cache/bd55fd0bdad535ef26f5252252852e92.png) до
до ![[0,N]](/sites/default/files/tex_cache/c06e42915defe7761a798b4211cb5a82.png) ).
). - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Дан номер строки
столбцов. Дан номер строки  и номер столбца
и номер столбца  , при помощи которых исходная матрица разбивается на четыре части. Найти сумму элементов каждой части.
, при помощи которых исходная матрица разбивается на четыре части. Найти сумму элементов каждой части. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Определить, сколько нулевых элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из
столбцов. Определить, сколько нулевых элементов содержится в каждом столбце и в каждой строке матрицы. Результат оформить в виде матрицы из 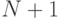 строк и
строк и 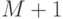 столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Дан номер строки
столбцов. Дан номер строки  и номер столбца
и номер столбца  , при помощи которых исходная матрица разбивается на четыре части. Найти среднее арифметическое элементов каждой части.
, при помощи которых исходная матрица разбивается на четыре части. Найти среднее арифметическое элементов каждой части. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Все элементы имеют целый тип. Дано целое число
столбцов. Все элементы имеют целый тип. Дано целое число  . Определить, какие строки имеют хотя бы одно такое число, а какие не имеют.
. Определить, какие строки имеют хотя бы одно такое число, а какие не имеют. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Исключить из матрицы столбец с номером
столбцов. Исключить из матрицы столбец с номером  . Сомкнуть столбцы матрицы.
. Сомкнуть столбцы матрицы. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Добавить к матрице столбец чисел и вставить его под номером
столбцов. Добавить к матрице столбец чисел и вставить его под номером  .
. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Добавить к элементам каждого столбца такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из
столбцов. Добавить к элементам каждого столбца такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из 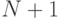 строк и
строк и  столбцов.
столбцов. - Выполнить обработку элементов прямоугольной матрицы
 , имеющей
, имеющей  строк и
строк и  столбцов. Добавить к элементам каждой строки такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из
столбцов. Добавить к элементам каждой строки такой новый элемент, чтобы сумма положительных элементов стала бы равна модулю суммы отрицательных элементов. Результат оформить в виде матрицы из  строк и
строк и 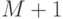 столбцов
столбцов