НОУ ИНТУИТ | Практикум по алгоритмизации и программированию на Python. Лекция 2: Основные алгоритмы и их реализация на Python

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.04.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 39 студентам

| Поделиться |

Поддержать программу

2.3 Циклические алгоритмы. Обработка последовательностей и одномерных массивов

Циклом называется фрагмент алгоритма или программы, который может повторяться несколько раз (в том числе и нуль раз). Каждая циклическая конструкция начинается заголовком цикла и заканчивается конечным оператором. Между ними располагаются операторы, называемые "телом цикла". Количество повторений выполнения команд (операторов), составляющих тело цикла, определяется условием окончания цикла. Условием окончания может быть достижение некоторого значения специальной переменной, называемой параметром цикла (переменной цикла), или выполнение (прекращение выполнения) некоторого условия.

Рис. 2.9. Пример блок-схемы цикла с параметром

Для организации циклов с параметром в языках программирования используется составной оператор FOR ("для"), а в циклах с условием чаще всего используется составной оператор WHILE ("пока").

В случае цикла с параметром количество повторений ("оборотов") цикла известно заранее и задаётся специальным выражением в заголовке цикла, а в случае цикла с условием при каждом следующем повторении требуется проверять условие прекращения цикла.

Если при написании операторов в теле цикла допущена ошибка, условие прекращения цикла может не выполниться никогда и цикл окажется бесконечным ("программа зациклится").

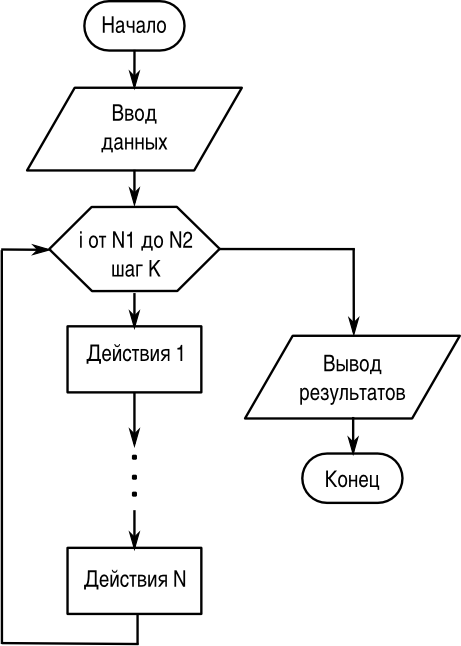
Пример блок-схемы цикла с параметром (переменной) показан на рис. 2.9, а пример блок-схемы цикла с условием окончания — на рис. 2.10. Для обозначения заголовка цикла с параметром используется специальный графический элемент — блок модификации, в котором указывается правило изменения параметра цикла.

Для работы с одномерными массивами целесообразно использовать циклы с параметром, поскольку до начала цикла может быть определено количество повторений. В этом случае цикл с параметром требуется для ввода элементов массива, а для выполнения каких-либо действий с этими элементами и вывода результатов также могут потребоваться циклы.

Рис. 2.10. Пример блок-схемы цикла с условием

В блок-схеме на рис. 2.10 действия повторяются, пока выполняется некоторое условие. Когда условие перестаёт выполняться, цикл завершается.

Такие циклы целесообразно использовать в ситуации, когда данные вводятся (поступают из какого-то источника), пока не произойдёт некоторое событие. При этом всю обработку чаще всего приходится выполнять "на лету", не создавая массив, поскольку количество элементов заранее неизвестно.

Рассмотрим типичные задачи, решение которых требует вычислений в цикле.

Задача 1. Дан одномерный массив числовых значений, насчитывающий элементов. Найти среднее арифметическое элементов массива.

Постановка задачи:

Дано:

– количество элементов в массиве;
- индекс элемента массива (параметр цикла).
– элемент массива;

Найти:

– сумма элементов массива
– среднее арифметическое элементов массива, C=S/N.

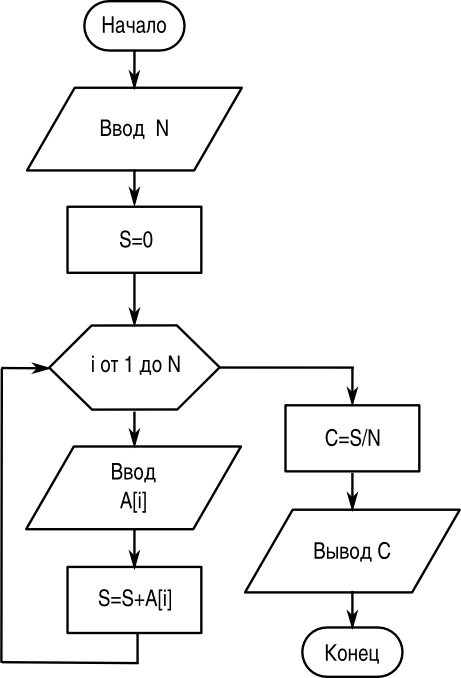
Блок-схема алгоритма показана на рис. 2.11.

Текст программы на "псевдоязыке":

Рис. 2.11. Блок-схема алгоритма вычисления среднего значения в массиве

ввод N
S=0
нц для i от 1 до N
	ввод A[i]
	S=S+A[i]
кц
C=S/N
вывод C

Здесь нц и кц обозначают, соответственно, начало и конец цикла, строка с нц является заголовком цикла. Как видно из текста, указываются начальное и конечное значение переменной цикла, которая обязательно должна быть целым числом. В приведённой здесь записи переменная цикла увеличивается на 1 при каждом повторении ("шаг переменной цикла" равен 1). Если требуется шаг, не равный 1, это указывается специально.

Тело цикла состоит из двух операторов — ввода очередного числа и прибавления этого числа к текущему значению суммы.

На Python можно написать практически то же самое (с учётом особенностей, связанных с использованием функции range()).

# -*- coding: utf-8 -*-

#

N=input('Количество элементов: ')

S=0

for i in range(N-1) :

a=input('Введите число: ')

S=S+a

C=S/N

print'Результат:',C

Поскольку диапазон чисел, формируемых функцией range(), начинается с 0, то верхней границей должно быть N -1 . Так как массив хранить нет необходимости, можно просто вводить числа и добавлять их к текущему значению суммы.

Тело цикла начинается после символа ":", и все операторы тела цикла в Python должны иметь одинаковый отступ от начала строки. Как только отступ исчезает, Python считает, что тело цикла закончилось.

А вот вариант решения этой же задачи на Python с использованием списка и методов списка.

# -*- coding: utf-8 -*-

#

N=input('Количество элементов: ')

S=0

lst=[]

for i in range(N-1) :

a=input('Введите число: ')

lst.append(a)

C=sum(lst)/N

print'Результат:',C

В этом варианте формируется список, а сумма элементов списка вычисляется с помощью встроенной функции. Программа увеличилась на одну строку (создание пустого списка), но зато мы научились формировать список в цикле.

Задача 2. Определить, является ли введённая строка палиндромом ("перевёртышем") типа ABBA, kazak и пр.

Постановка задачи: Требуется сравнивать попарно символы с начала и с конца строки (первый и последний, второй и предпоследний и т.д.). Если в каждой такой паре символы одинаковы, строка является палиндромом. Соответственно, каждая проверка пары символов должна получить некоторый признак (flag — "флаг"), который будет равен 1, если символы в паре совпадают и 0, если не совпадают. Окончательный результат обработки строки получится как произведение всех значений "флагов". Если хотя бы один раз "флаг" оказался равен нулю, строка палиндромом не является и произведение всех "флагов" окажется равным 0. Количество пар не превышает половины длины строки (точно равно половине длины для строк с чётным количеством символов и результат целочисленного деления длины строки на 2 для строк с нечётным количеством символов, поскольку "центральный" символ строки с нечётным количеством символов очевидно совпадает сам с собой).

Блок-схема алгоритма показана на рис. 2.12.

увеличить изображение
Рис. 2.12. Блок-схема алгоритма определения палиндрома

Текст программы на "псевдоязыке":

ввод S
flag=1
L=длина(S)
N=L div 2
нц для i от 1 до N
	если S[i]=S[L-i +1] то
		k=1
	иначе
		k=0
	конец если
	flag=flag *k
кц
если flag=1 то
	вывод 'Палиндром'
иначе
	вывод 'Не палиндром!'
конец если

При проверке каждой пары устанавливается коэффициент , который затем умножается на текущее значение "флага". Окончательный вывод делается по итоговому значению "флага".

Текст программы на Python может быть очень похож на текст на псевдоязыке.

# -*- coding: utf-8 -*-

#

s1=raw_input('Исходная строка: ')

# Определяем длину строки

L=len(s1)

flag=1

for i in range(L//2):

if s1[i]==s 1[-i-1]:

k=1

else:

k=0

flag=flag*k

if flag==1:

print 'Палиндром'

else:

print 'Не палиндром!'

Для ввода строки использован оператор raw_input(), при этом не требуется записывать строку в кавычках.

Небольшие синтаксические особенности всё-таки есть — условие равенства двух переменных записывается знаком "==", начало каждого составного оператора обозначается символом ":", и, как всегда, необходимо следить за отступами. Кроме того, чтобы отсчитывать символы с конца строки, использованы "отрицательные" индексы элементов строки.

Однако использование особенностей строк в Python, их функций и методов, позволяет решить эту задачу более изящно. Например, так.

# -*- coding: utf-8 -*-

#

s1=raw_input('Исходная строка: ')

lst=list(s1)

lst.reverse()

s 2=' '.join(lst)

if s1==s2:

print'Палиндром'

else:

print'Не палиндром!'

Рис. 2.13. Блок-схема алгоритма обработки последовательности

Здесь исходная строка преобразуется в список, затем список "переворачивается" и из него с помощью пустой "строки-объединителя" формируется новая строка. Затем строки сравниваются. Цикл оказывается не нужен! Всю работу делает Python.

Если количество повторений операций заранее неизвестно, но известно условие прекращения выполнения операций, используется цикл (составной оператор) WHILE. Покажем его использование на следующем примере.

Задача 3. Последовательно вводятся ненулевые числа. Определить сумму положительных и сумму отрицательных чисел. Закончить ввод чисел при вводе 0.

Задача настолько проста, что дополнительных уточнений в качестве постановки задачи не требуется. Пусть сумма положительных чисел называется SP, а сумма отрицательных чисел — SN.

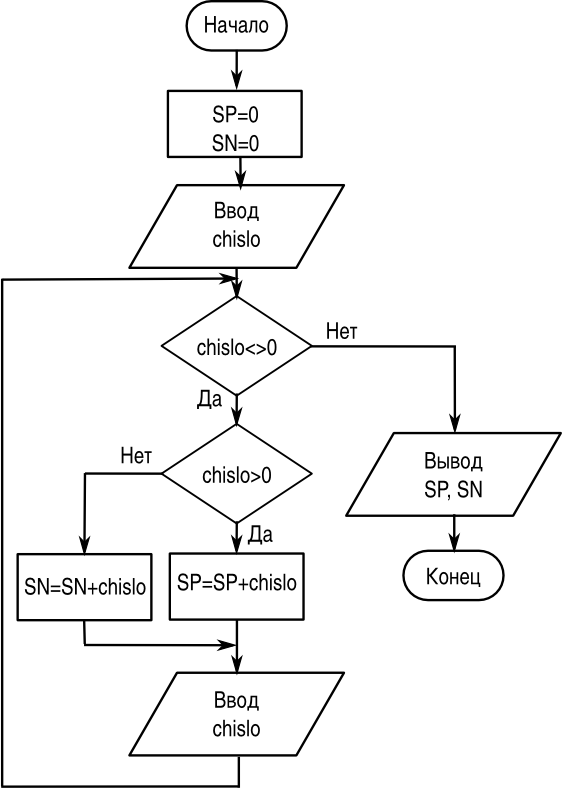
Блок-схема алгоритма показана на рис. 2.13.

Текст программы на "псевдоязыке":

SP=0
SN=0
ввод chislo
нц пока chislo <> 0
	если chislo > 0 то
		SP=SP+chislo
	иначе
		SN=SN+chislo
	конец если
ввод chislo
кц
вывод SP
вывод SN

Условие "неравенства" в языках программирования Pascal и BASIC обозначается как "<>", поэтому здесь сохранено это обозначение.

Следует обратить внимание, что проверяемое число нужно определить до начала цикла, поскольку возможна ситуация, что неопределённое значение окажется равным 0 и программа закончится, не успев начаться. А потом числа вводятся в цикле и каждое вновь поступившее число сравнивается с 0 (после ввода каждого числа следует проверка условия). Порядок операций и проверок в цикле WHILE может оказаться важным для получения верного результата.

Текст программы на Python не имеет каких-то существенных особенностей. Для удобства чтения программа поделена на "блоки" с помощью символа комментария.

# -*- coding: utf-8 -*-

#

SP=0

SN=0

#

chislo=input('Следующее число: ')

#

while chislo!=0:

if chislo > 0 :

SP=SP+chislo

else:

SN=SN+chislo

chislo=input('Следующее число: ')

#

print'Сумма положительных:',SP

print'Сумма отрицательных:',SN

Рис. 2.14. Алгоритм сортировки "методом пузырька"

2.3.1 Сортировка массива

Задача сортировки, а также задача поиска максимального или минимального элемента в массиве встречается довольно часто. Средствами Python такие задачи решаются очень просто, но тем не менее рассмотрим общую задачу сортировки массива.

Под сортировкой понимается процедура, в результате выполнения которой изменяется исходный порядок следования данных. Причём новый порядок их следования отвечает требованию возрастания или убывания значений элементов одномерного массива. Например, при сортировке по возрастанию из одномерного массива[3 1 0 5 2 7] получается массив[0 1 2 3 5 7]. Возможны и более сложные критерии сортировки. Символьные данные обычно сортируются в алфавитном порядке.

Один из наиболее наглядных методов сортировки — "метод пузырька".

Пусть необходимо упорядочить элементы массива из элементов по возрастанию.

Просматривая элементы массива "слева направо" (от первого элемента к последнему), меняем местами значения каждой пары соседних элементов в случае неравенства A[i] > A[i + 1] , передвигая тем самым наибольшее значение на последнее место. Следующие просмотры начинаем опять с первого элемента массива, последовательно уменьшая на единицу количество просматриваемых элементов. 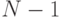Процесс заканчивается после N - 1 просмотра.

Метод получил такое название, потому что каждое наибольшее значение как бы всплывает вверх.

Фрагмент блок-схемы алгоритма показан на рис. 2.14.

Действие $A[i] \leftrightarrow A[i + 1]$ означает перестановку значений элементов массива.

Текст соответствующего фрагмента программы на "псевдоязыке":

ввод N, A
нц для m от N-1 до 1 шаг -1
	нц для i от 1 до m
		если A[i] > A[i +1] то
		X=A[i]
		A[i]=A[i +1]
		A[i +1]=X
		конец если
	кц
кц
вывод A

В этом фрагменте для перестановки значений элементов массива используется промежуточная переменная.

Задача поиска максимального элемента в массиве решается следующим образом. Пусть maxA — требуемое значение максимального элемента. Сначала присваиваем переменной maxA значение первого элемента массива, потом сравниваем первый элемент со следующим. Если следующий элемент (второй) больше первого, присваиваем его значение переменной maxA, а если нет — переходим к следующему (третьему элементу) и т. д.

Аналогично решается задача поиска минимального элемента в массиве.

В Python эти алгоритмы уже реализованы в функциях max(), min() и в методе sort() (метод sort() сортирует список по возрастанию значений элементов).

2.3.2 Задачи для самостоятельного решения

Составьте блок-схему поиска максимального элемента в одномерном массиве.
Нарисуйте полную блок-схему алгоритма сортировки массива "методом пузырька".
Дан одномерный массив числовых значений, насчитывающий элементов. Поменять местами элементы, стоящие на чётных и нечётных местах: $A[1] \leftrightarrow A[2]; A[3] \to A[4] ...$
Дан одномерный массив числовых значений, насчитывающий элементов. Выполнить перемещение элементов массива по кругу вправо, т. е. $A[1] \to A[2]; A[2] \to A[3]; ... A[n] \to A[1]$ .
Дан одномерный массив числовых значений, насчитывающий элементов. Поменять местами первую и вторую половины массива.
Дан одномерный массив числовых значений, насчитывающий элементов. Поменять местами группу из элементов, начинающихся с позиции с группой из элементов, начинающихся с позиции .
Дан одномерный массив числовых значений, насчитывающий элементов. Вставить группу из новых элементов, начиная с позиции .
Дан одномерный массив числовых значений, насчитывающий элементов. Сумму элементов массива и количество положительных элементов поставить на первое и второе место.
Дан одномерный массив числовых значений, насчитывающий элементов. Исключить из него элементов, начиная с позиции .
Дан одномерный массив числовых значений, насчитывающий элементов. Исключить все нулевые элементы.
Дан одномерный массив числовых значений, насчитывающий элементов. После каждого отрицательного элемента вставить новый элемент, равный квадрату этого отрицательного элемента.
Дан одномерный массив числовых значений, насчитывающий элементов. Определить, образуют ли элементы массива, расположенные перед первым отрицательным элементом, возрастающую последовательность.
Дан одномерный массив числовых значений, насчитывающий элементов. Определить, образуют ли элементы массива, расположенные перед первым отрицательным элементом, убывающую последовательность.
Дан одномерный массив числовых значений, насчитывающий элементов. Из элементов исходного массива построить два новых. В первый должны входить только элементы с положительными значениями, а во второй — только элементы с отрицательными значениями.
Дан одномерный массив числовых значений, насчитывающий элементов. Добавить столько элементов, чтобы элементов с положительными и отрицательными значениями стало бы поровну.
Дан одномерный массив числовых значений, насчитывающий элементов. Добавить к элементам массива такой новый элемент, чтобы сумма элементов с положительными значениями стала бы равна модулю суммы элементов с отрицательными значениями.
Дан одномерный массив числовых значений, насчитывающий элементов. Дано положительное число . Разделить это число между положительными элементами массива пропорционально значениям этих элементов и добавить полученные доли к соответствующим элементам.
Дан одномерный массив числовых значений, насчитывающий элементов. Исключить из массива элементы, принадлежащие промежутку .
Дан одномерный массив числовых значений, насчитывающий элементов. Вместо каждого элемента с нулевым значением поставить сумму двух предыдущих элементов массива.
Дан одномерный массив числовых значений, насчитывающий элементов. Определить, имеются ли в массиве два подряд идущих нуля.
Дан одномерный массив числовых значений, насчитывающий элементов. Подсчитать количество чисел, делящихся на 3 нацело, и среднее арифметическое чисел с чётными значениями. Поставить полученные величины на первое и последнее места в массиве (увеличив массив на 2 элемента).
Заданы строк символов, которые вводятся с клавиатуры. Найти количество символов в самой длинной строке. Выровнять строки по самой длинной строке, поставив перед каждой строкой соответствующее количество звёздочек.
Заданы строк символов, которые вводятся с клавиатуры. Из заданных строк, каждая из которых представляет одно слово, составить одну длинную строку, разделяя слова пробелами.
Заданы строк слов, которые вводятся с клавиатуры. Подсчитать количество гласных букв в каждой из заданных строк.
Заданы строк слов, которые вводятся с клавиатуры (в каждой строке – одно слово). Вводится слог (последовательность букв). Подсчитать количество таких слогов в каждой строке.
Заданы строк слов, которые вводятся с клавиатуры (в каждой строке – одно слово). Вводится слог (последовательность букв). Удалить данный слог из каждой строки.
Заданы строк символов, которые вводятся с клавиатуры. Напечатать все центральные буквы строк нечетной длины.
Заданы строк символов, которые вводятся с клавиатуры. Каждая строка содержит слово. Записать каждое слово в разрядку (вставить по пробелу между буквами).
Задана строка символов, в которой встречается символ ".". Поставить после каждого такого символа системное время ПК.
Заданы строк, которые вводятся с клавиатуры. Подсчитать количество пробелов в каждой из строк.
Заданы строк символов, которые вводятся с клавиатуры. Каждая строка представляет собой последовательность символов, включающих в себя вопросительные знаки. Заменить в каждой строке все имеющиеся вопросительные знаки звёздочками.
Последовательно вводятся числа. Определить сумму чисел с нечётными номерами и произведение чисел с чётными номерами (по порядку ввода). Подсчитать количество слагаемых и количество сомножителей. При вводе числа 55555 закончить работу.
Определить сумму вводимых положительных чисел. Причём числа с нечётными номерами (по порядку ввода) суммировать с обратным знаком, а числа с чётными номерами перед суммированием возводить в квадрат. Подсчитать количество слагаемых. При вводе первого отрицательного числа закончить работу.
Даны число и число . Определить сумму чисел меньше , произведение чисел больше и количество чисел в диапазоне значений и . При вводе числа равного или , закончить работу.
Суммировать вводимые числа, среди которых нет нулевых. При вводе нуля обеспечить вывод текущего значения суммы. При вводе числа 99999 закончить работу.
Вводятся положительные числа. Определить сумму чисел, делящихся на положительное число нацело. При вводе отрицательного числа закончить работу.
Для вводимых чисел определить процент положительных и отрицательных чисел. При вводе числа -65432 закончить работу.