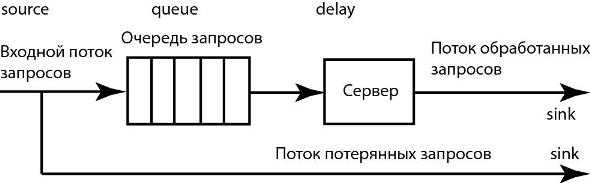
Модель обработки запросов сервером

Решение обратной задачи

Для решения обратной задачи возьмем количество запросов, ожидаемое время обработки которых нужно определить, N=29 - результат решения прямой задачи.

Программа модели приведена ниже.

; Обработка запросов сервером. Обратная задача
; Задание исходных данных
T1_	EQU	120		; Средний интервал поступления запросов, с
S1_	EQU	60000000	; Среднее значение вычислительной сложности запросов, оп
S2_	EQU	200000	; Стандартное отклонение вычислительной сложности запросов, оп
Q_	EQU	600000	; Средняя производительность сервера, оп/c
Emk	EQU	5		; Ёмкость входного буфера
Koef	EQU	1		; Коэффициент изменения характеристик нормального распределения
Koef1	EQU	1		; Коэффициент учета дробной части
N_	EQU	29		; Количество запросов
; Сегмент имитации обработки запросов
	GENERATE	(Exponential(1,0,T1_))	; Источник запросов
KolZap	TEST L	Q$Server,Emk,PotZap   ; Занят ли буфер? 	QUEUE	Server	; Встать в очередь к серверу
	SEIZE		Server	; Занять сервер
	DEPART	Server	; Покинуть очередь к серверу
	ADVANCE	((Normal(2,(S1_#Koef),(S2_#Koef)))/Q_) ; Имитация обработки запроса
	RELEASE	Server	; Освободить сервер
	TRANSFER	,ObrZap	; Запрос отправляется в сегмент завершения моделирования
PotZap	TERMINATE		; Потерянные запросы
; Сегмент организации завершения моделирования и расчета результатов
ObrZap	TEST L	X$Prog,TG1,Met1	; Если X$Prog < TG1,
	SAVEVALUE	Prog,TG1	; то X$Prog = TG1
	SAVEVALUE	NZap,0  ; Обнуление счетчика обработанных запросов
Met1	SAVEVALUE	NZap+,1  ; Счет количества обработанных запросов
	TEST E		X$NZap,N_,Ter1  ; Если X$NZap = N_, то
	TEST E		TG1,1,Met2  ; если TG1 = 1, то
	SAVEVALUE	VerObr,(N$ObrZap/N$KolZap) 	; расчет и сохранение в ячейке VerObr вероятности обработки запросов
	SAVEVALUE	TimeNZap,((AC1-X$AC2)/(X$Prog#Koef1))
;расчет и сохранение в ячейке TimeNZap времени обработки запросов
	SAVEVALUE	AC2,AC1  ; Запомнить абсолютное модельное время в ячейке АС2
Met2	SAVEVALUE	NZap,0  ; Обнуление счетчика обработанных запросов
	TERMINATE	1
Ter1	TERMINATE
	START	1000,NP	; Прогоны до установившегося режима
	RESET			; Сброс накопленной статистики
	START	9604		; Количество прогонов модели

При решении обратной задачи один прогон определяется заданным количеством запросов N_, которые нужно обработать сервером, а не временем моделирования. Для этого организован счетчик обработанных запросов в виде сохраняемой ячейки X$NZap. Как только содержимое X$NZap = N_, из счетчика завершений вычитается единица. Таким образом, фиксируется один прогон модели. После этого ячейка X$NZap обнуляется и начинается очередной прогон.

Для расчета времени обработки заданного количества запросов используется арифметическое выражение (AC1-X$AC2)/X$Prog. В состав этого выражения входят абсолютное модельное время АС1 и опять количество прогонов. Запоминается количество прогонов также как и при решении прямой задачи.

Кроме этого, в арифметическом выражении есть сохраняемая ячейка X$AC2. Дело в том, что команда RESET не влияет на абсолютное модельное время АС1. Время же выполнения 1000 прогонов до установившегося режима не должно участвовать в расчёте. Поэтому оно запоминается, а затем вычитается из абсолютного модельного времени выполнения 1000 + 9604 = 10604 прогонов. Число прогонов до установившегося режима может быть и другим.

В результате моделирования получим среднее время обработки 29 запросов 3579,401 с.

Фрагмент из отчета моделирования приведен ниже:

SAVEVALUE               RETRY       VALUE
 PROG                     0       9604.000
 NZAP                     0              0
 VEROBR                   0          0.971
 TIMENZAP                 0       3579.401

А почему не 3600 сек? Ведь это же время моделирования было задано при решении прямой задачи? Потому что мы отбросили дробную часть, т. е. взяли 29, а не 29,161. Как же поступить, чтобы учесть и отброшенную дробную часть? Ведь в счётчике фиксируются обработанные запросы только целыми числами, а не дробными?

Для учёта десятых долей дробной части зададим N_ = 291, т. е. увеличим в 10 раз. Это нужно учесть и в арифметическом выражении: ((AC1-X$AC2)/(X$Prog#Koef1)). Переменной пользователя Koef1 задается значение 10. По завершении моделирования получим 3594,826 с. Этот результат уже ближе к 3600.

Для учёта сотых долей дробной части установим N_ = 2916, а Koef1 = 100. Получим 3602,099.

Вероятность обработки запросов в обоих случаях практически одна и та же, т. е. 0,971. Однако время моделирования существенно возрастает: 2 с, 21 с и 3 мин 34 c соответственно, т. е. более чем в 10 и 100 раз.

В примере обратной задачи также показано, что арифметические выражения можно не описывать отдельно до блоковой части программы вместе с заданием исходных данных (как в программе модели прямой задачи), а сразу записывать в соответствующих блоках, заключив в скобки (скобки можно и не ставить, но лучше это делать).

Например (см. сегмент организации завершения моделирования и расчета результатов):

ADVANCE	((Normal(2,(S1_#Koef),(S2_#Koef)))/Q_)       ;  Розыгрыш времени обработки запроса
SAVEVALUE	VerObr,(N$ObrZap/N$KolZap))  	 ; Расчет вероятности обработки запросов
SAVEVALUE	TimeNZap,((AC1-X$AC2)/(X$Prog#Koef1)) ; Расчет среднего времени обработки запросов

Модель в AnyLogic

Постановка задачи

Сервер обрабатывает запросы, поступающие с автоматизированных рабочих мест с интервалами, распределенными по показательному закону со средним значением 2 мин. Время обработки сервером одного запроса распределено по экспоненциальному закону со средним значением 3 мин. Сервер имеет входной буфер ёмкостью 5 запросов.

Построить имитационную модель для определения математического ожидания времени и вероятности обработки запросов.

Сервер представляет собой однофазную систему массового обслуживания разомкнутого типа с ограниченной входной емкостью, то есть с отказами, и абсолютной надёжностью (Рис. 1.11).

На Рис. 1.11 приведены также объекты AnyLogic, которые будут использованы для создания диаграммы процесса. На них мы остановимся позже. Приступим к созданию диаграммы процесса.

увеличить изображение
Рис. 1.11. Сервер как система массового обслуживания

Создание диаграммы процесса

1. Выполните Файл/Создать/Модель на панели инструментов. Появится диалоговое окно Новая модель (Рис. 1.12).
2. Задайте имя новой модели. В поле Имя модели введите Server.
3. Выберите каталог, в котором будут сохранены файлы модели. Если хотите сменить предложенный по умолчанию каталог на какой-то другой, то можете ввести путь к нему в поле Местоположение или выбрать этот каталог с помощью диалога навигации по файловой системе, открывающегося нажатием кнопки Выбрать.
   

   
   Рис. 1.12. Диалоговое окно Новая модель
4. Щёлкните кнопку Готово. Откроется пользовательский интерфейс (Рис. 1.13). Остановимся на нём.
5. В левой части рабочей области находятся панель Проекты и панель Палитра. Панель Проект обеспечивает навигацию по элементам моделей, открытых в текущий момент времени. Модель организована иерархически. Она отображается в виде дерева. Сама модель образует верхний уровень дерева. Эксперименты, классы активных объектов и Java классы образуют следующий уровень. Элементы, входящие в состав активных объектов, вложены в соответствующую подветвь дерева класса активного объекта и т. д.
6. Панель Палитра (левый вертикальный столбец) содержит разделённые по категориям элементы, которые могут быть добавлены на графическую диаграмму типа агентов или эксперимента. На Рис. 1.13 раскрыта палитра Презентация. Для того чтобы открыть нужную палитру, следует подвести курсор к иконке и щелкнуть мышью. Иконка становится светлой.
7. В правой части отображается панель Свойства. Панель Свойства используется для просмотра и изменения свойств выбранного в данный момент элемента (или элементов) модели.
8. В центре рабочей области AnyLogic размещён графический редактор диаграммы агента Main.
   

   
   увеличить изображение
   Рис. 1.13. Пользовательский интерфейс
9. При работе не забывайте сохранять производимые изменения с помощью кнопки панели инструментов Сохранить .
10. Создайте диаграмму процесса. Для этого в Палитре выделите Библиотеку моделирования процессов (Рис. 1.14). Из неё перетащите объекты на диаграмму и соедините, как показано на Рис. 1.15. Для добавления объекта на диаграмму, надо щёлкнуть его мыщью и, не отпуская её, перетащить в графический редактор.
11. При перетаскивании объектов вы можете видеть, как появляются соединительные линии между объектами. Обращайте внимание на то, чтобы эти линии, если необходимо, соединяли только порты, находящиеся с правой или левой стороны иконок. Если у вас не получится автоматическое соединение нужных объектов, дважды щёлкните начальный порт. Он станет зелёным. Протащите курсор к конечному порту. Он также станет зелёным. Для завершения процесса соединения дважды щёлкните конечный порт.
    

    
    увеличить изображение
    Рис. 1.14. Библиотека моделирования процессов
    

    
    увеличить изображение
    Рис. 1.15. Диаграмма системы массового обслуживания

    Дадим краткую характеристику объектов диаграммы.
12. Объект Source генерирует заявки определенного типа. Обычно он используется в качестве начальной точки диаграммы процесса, формализующей поток заявок. В нашем примере заявками будут запросы на обработку сервером, а объект Source будет моделировать их поступление.
13. Объект Queue моделирует очередь заявок, ожидающих приема объектами, следующими за данным в диаграмме процесса. В нашем случае он будет моделировать очередь запросов, ожидающих освобождения сервера.
14. Объект Delay задерживает заявки на заданный период времени. Он представляет в нашей модели сервер, обрабатывающий запросы.
15. Объект Sink уничтожает поступившие заявки. Обычно он используется в качестве конечной точки потока заявок (и диаграммы процесса соответственно).