|
Коллеги, спасибо за очень информативный и полезный курс. Прошёл три лекции. Столкнулся с проблемой, что обе модели не могут закончить расчёт по причине ограничения бесплатной версии "создано максимально допустимое число динамически создаваемых агентов (50000)". По скриншотам Лекции 2 видно, что да, модель создает гораздо больше 50000 агентов. В принципе, мне то и диплом не особо нужен. Но хотелось бы выполнить практические работы. Нет ли возможности откорректировать эту проблему? Или может я чего не так делаю? Еще раз спасибо за прекрасный курс! |
Модель обработки запросов сервером
Модель в GPSS World
При имитационном моделировании с использованием специальных инструментальных средств, например, GPSS World, в общем случае решаются две задачи. Назовем их прямой и обратной.
Прямая задача заключается в нахождении оценки математического ожидания какого-либо показателя моделируемой системы при заданном времени ее функционирования.
Обратная задача состоит в определении оценки математического ожидания времени функционирования системы, за которое какой-либо её показатель достигает заданного значения.
Решение этих задач, особенно обратной задачи, имеет свои особенности. Рассмотрим эти особенности далее на примерах. Начнём построение GPSS-моделей с прямой задачи.
Решение прямой задачи
Постановка задачи
Сервер обрабатывает запросы, поступающие с автоматизированных рабочих мест (АРМ) с интервалами, распределенными по показательному закону со средним значением T1 = 2 мин. Сервер имеет входной буфер ёмкостью 5 запросов.
Вычислительная сложность запросов подчинена нормальному закону с математическим ожиданием  оп и среднеквадратическим отклонением
оп и среднеквадратическим отклонением 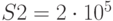 оп. Производительность сервера
оп. Производительность сервера 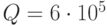 оп/с. В случае полной занятости входного буфера поступающий запрос теряется.
оп/с. В случае полной занятости входного буфера поступающий запрос теряется.
Построить имитационную модель обработки запросов сервером для определения оценки математического ожидания количества запросов (дальше - количества запросов), обработанных сервером за время функционирования T = 1 час, и оценки математического ожидания вероятности обработки запросов (дальше - вероятности обработки запросов).
Уяснение задачи моделирования
Сервер представляет собой однофазную систему массового обслуживания разомкнутого типа с ожиданием и с отказами.
В модели для имитации источника запросов следует использовать блок GENERATE, для имитации сервера как одноканального устройства - блоки SEIZE и RELEASE, для имитации буфера - QUEUE и DEPART, обработки запросов - ADVANCE.
В модели должны быть следующие элементы:
- задание исходных данных;
- описание арифметических выражений;
- сегмент имитации поступления и обработки запросов;
- сегмент задания времени моделирования и расчета результатов моделирования.
Серверу дадим имя Server. Для вывода из модели транзактов, имитирующих обработанные и потерянные запросы, используем блоки TERMINATE с метками ObrZap и PotZap соответственно. Для счета количества всех запросов используем метку KolZap.
Выберем масштаб: 1 единице масштабного времени соответствует 1 с. Так как среднее значение интервалов поступления запросов ,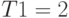 мин. то теперь это будет 120 ед. мод. времени.
мин. то теперь это будет 120 ед. мод. времени.
Рассчитаем количество прогонов, которые нужно выполнить в каждом наблюдении, т. е. проведем так называемое тактическое планирование эксперимента. Пусть результаты моделирования (вероятность обработки запросов) нужно получить с доверительной вероятностью  и точностью
и точностью 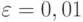 Расчет проведем для худшего случая, т. е. при вероятности
Расчет проведем для худшего случая, т. е. при вероятности 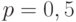 , так как до эксперимента
, так как до эксперимента  неизвестно:
неизвестно:
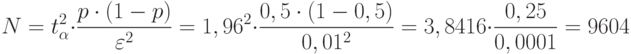
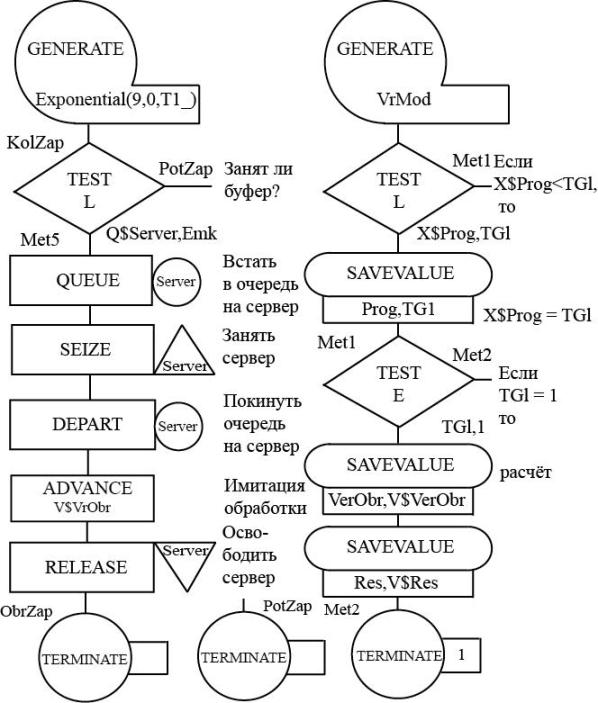
Блок-диаграмма модели
Построим блок-диаграмму модели для решения прямой задачи, т. е. сегмент имитации поступления и обработки запросов и сегмент задания времени моделирования и расчета результатов моделирования (Рис. 1.1).
Блок-диаграмма представляет собой набор стандартных блоков. Она строится так. Из множества блоков выбирают нужные, и далее выстраивают их в диаграмму для того, чтобы в процессе функционирования модели они как бы взаимодействовали друг с другом. Диаграмма сопровождается необходимыми комментариями. Использование блоков при построении моделей зависит от логических схем работы реальных систем, моделируемых на ЭВМ.
Теперь приступим к написанию программы модели.
Программа модели
Для задания исходных данных используем переменные пользователя. Они задаются с помощью команды EQU. Переменным пользователя даны такие же имена, как и в постановке задачи, но добавлен знак подчеркивания. Например, T1_, S1_ и т. д. Время моделирования зададим переменной пользователя VrMod.
Арифметическая переменная для расчета времени обработки VrObr запроса на сервере:
VrObr VARIABLE (Normal(2,(S1_#Koef),(S2_#Koef))))/Q_
Переменная пользователя Koef введена для удобства изменения (пропорционального изменения) характеристик нормального закона распределения, которому подчиняется вычислительная сложность запросов. Особенно целесообразно использование этой переменной при проведении экспериментов.
Вероятность обработки VerObr запросов на сервере будем определять как отношение количества обработанных N$ObrZap запросов к количеству всего поступивших N$KolZap запросов:
VerObr VARIABLE N$ObrZap/N$KolZap
В арифметическом выражении VerObr, например, N$ObrZap - системный числовой атрибут - количество транзактов, вошедших в блок с меткой ObrZap, а N$KolZap - количество транзактов, вошедших в блок с меткой KolZap.
Количество обработанных запросов определяется арифметическим выражением:
Res VARIABLE INT(N$ObrZap/X$Prog)
Все необходимое для написания программы модели имеется. Напишем программу модели для решения прямой задачи.
; Обработка запросов сервером. Прямая задача ; Задание исходных данных T1_ EQU 120 ; Средний интервал поступления запросов, с S1_ EQU 60000000 ; Среднее значение вычислительной сложности запросов, оп S2_ EQU 200000 ; Стандартное отклонение вычислительной сложности запросов, оп Q_ EQU 600000 ; Средняя производительность сервера, оп/с Emk EQU 5 ; Ёмкость входного буфера Koef EQU 1 ; Коэффициент изменения характеристик нормального распределения VrObr VARIABLE (Normal(9,(S1_#Koef),(S2_#Koef)))/Q_ VerObr VARIABLE N$ObrZap/N$KolZap Res VARIABLE INT(N$ObrZap/X$Prog) VrMod EQU 3600 ; Время моделирования, 1 ед. мод. времени = 1 с. ; Сегмент имитации обработки запросов GENERATE (Exponential(2,0,T1_)) ; Источник запросов KolZap TEST L Q$Server,Emk,PotZap ; Занят ли буфер? QUEUE Server ; Встать в очередь к серверу SEIZE Server ; Занять сервер DEPART Server ; Покинуть очередь к серверу ADVANCE V$VrObr ; Имитация обработки запроса SAVEVALUE SumTime+,M1; Время обработки всех запросов RELEASE Server ; Освободить сервер ObrZap TERMINATE ; Обработанные запросы PotZap TERMINATE ; Потерянные запросы ; Сегмент задания времени моделирования и расчета результатов GENERATE VrMod TEST L X$Prog,TG1,Met1 ; Если X$Prog < TG1, SAVEVALUE Prog,TG1 ; то X$Prog = TG1 Met1 TEST E TG1,1,Met2 ; Если TG1 = 1, то SAVEVALUE VerObr,V$VerObr ; расчет и сохранение в ячейке VerObr вероятности обработки запросов SAVEVALUE Res,V$Res ; числа обработанных запросов SAVEVALUE TimeMean,(X$SumTime/N$ObrZap) Met2 TERMINATE 1 START 9604 ; Количество прогонов модели
При расчете количества обработанных запросов Res в арифметическом выражении N$ObrZap/X$Prog используется число прогонов. В арифметическом выражении указано не явное число прогонов, а в виде содержимого ячейки X$Prog. Число прогонов заносится предварительно в эту ячейку по завершении первого прогона модели, но до того момента, когда из счетчика завершений TG1 будет вычтена первая единица. В этом случае арифметическое выражение не зависит от числа прогонов, которое может меняться на различных этапах создания и эксплуатации модели, в том числе и в зависимости от исходных данных, а также от точности и достоверности результатов моделирования. Поскольку количество обработанных запросов не может быть дробным числом, то для получения целого числа, записываемого в ячейку Res, используется процедура INT из встроенной библиотеки.
Среднее время X$TimeMean обработки одного запроса определяется как отношение суммарного времени X$SumTime к количеству обработанных запросов N$ObrZap. В данной модели можно определять X$TimeMean как сумму средних времен обработки одного транзакта на сервере и среднего времени задержки в очереди.
Для уменьшения машинного времени расчет искомых показателей производится не после каждого прогона, а после завершения последнего прогона, т. е. когда содержимое счетчика завершений будет равно единице (TG1 = 1).