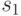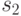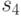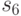|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Жадные алгоритмы поиска масок
СПР для единой маски, полученной сокращением СПР с помощью алгоритма1, для диагностического теста схемы C17 приведен в табл. 31.1.
Уточним верхнюю оценку объема маски, возвращаемой с помощью алгоритма 1. Но вначале сформулируем следующую лемму, которая потребуется для вывода этой оценки.
Лемма 1. На любом шаге  работы алгоритма 1 справедливо неравенство
работы алгоритма 1 справедливо неравенство
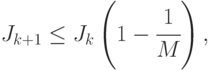 |
( 31.10) |
где  - объем минимальной маски заданного СПР.
- объем минимальной маски заданного СПР.
Доказательство. Заметим сначала, что для любой точки проверки 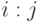 и для любого
и для любого  величина (31.9) неотрицательна. Действительно, (31.9) является конкретизацией выражения (31.6) , в котором вместо атрибута
величина (31.9) неотрицательна. Действительно, (31.9) является конкретизацией выражения (31.6) , в котором вместо атрибута  используется точка проверки
используется точка проверки 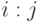 . Подставляя в (31.5) сначала (31.7) и (31.8), а затем (31.1) и (31.2) получим
. Подставляя в (31.5) сначала (31.7) и (31.8), а затем (31.1) и (31.2) получим
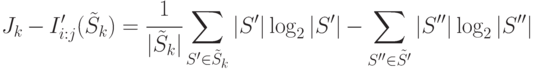 |
( 31.11) |
где 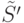 обозначает разбиение множества
обозначает разбиение множества 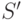 согласно значениям точки проверки
согласно значениям точки проверки 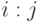 . Из того, что каждое слагаемое внешней суммы в (31.11) неотрицательно, следует неотрицательность (31.9). Отсюда вытекает, что последовательность
. Из того, что каждое слагаемое внешней суммы в (31.11) неотрицательно, следует неотрицательность (31.9). Отсюда вытекает, что последовательность

- невозрастающая.
Пусть после  итераций алгоритма 1 получена маска
итераций алгоритма 1 получена маска  и величина
и величина 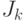 - среднее количество информации, необходимой для идентификации любого технического состояния из блоков разбиения
- среднее количество информации, необходимой для идентификации любого технического состояния из блоков разбиения 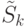 .
Пусть для того чтобы разбить блоки
.
Пусть для того чтобы разбить блоки 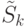 на одноэлементные подмножества оптимальным образом, требуется включение в маску
на одноэлементные подмножества оптимальным образом, требуется включение в маску  дополнительно минимум
дополнительно минимум 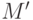 точек проверки. Тогда на следующей итерации алгоритма должно выполняться неравенство
точек проверки. Тогда на следующей итерации алгоритма должно выполняться неравенство
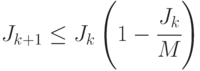 |
( 31.12) |
Т. к.  , из (31.12) следует (31.10).
, из (31.12) следует (31.10).
Теорема 2. Объем маски, полученной с помощью алгоритма 1, не превышает величины
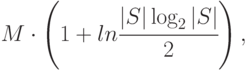
где  - объем минимальной маски заданного СПР.
- объем минимальной маски заданного СПР.
Доказательство. Согласно лемме 1

Исходя из представления (6.7), минимально-возможное ненулевое значение, которое может принимать 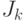 , равно
, равно  .
.
Пусть 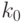 - максимальное целое число такое, что
- максимальное целое число такое, что
 |
( 31.13) |
Тогда для 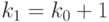 будет выполнено
будет выполнено  .Из (6.13) следует
.Из (6.13) следует

что влечет
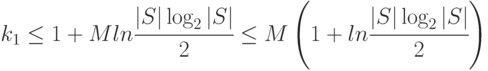
Следствие 1. Объем маски, полученной с помощью алгоритма 1, не превышает величины
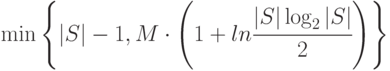
где  - объем минимальной маски данного СПР.
- объем минимальной маски данного СПР.
Справедливость следствия вытекает из теоремы 2 и замечания к алгоритму.
С точки зрения задачи оптимизации маски представляет интерес получение оценки глубины диагностирования с использованием маски, полученной с помощью алгоритма 1 при ограничении ее объема. В качестве оцениваемой величины возьмем значение диагностического разрешения 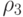 , определяемое равенством
, определяемое равенством
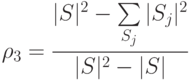
Теорема 3. Пусть для СПР существует оптимальная маска 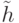 объема
объема  , а
, а 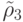 - величина диагностического разрешения при диагностировании с использованием
- величина диагностического разрешения при диагностировании с использованием  . Тогда, если
. Тогда, если  - маска объема
- маска объема  , найденная с помощью алгоритма 1, и
, найденная с помощью алгоритма 1, и 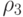 - диагностическое разрешение при диагностировании с помощью
- диагностическое разрешение при диагностировании с помощью 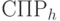 , то справедливо следующее неравенство
, то справедливо следующее неравенство
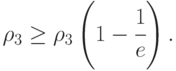
Доказательство. Разбиение 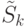 на
на  -ой итерации алгоритма можно интерпретировать как множество СПН, получаемое при диагностировании с помощью
-ой итерации алгоритма можно интерпретировать как множество СПН, получаемое при диагностировании с помощью 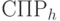 , где
, где  - маска, полученная после
- маска, полученная после  итераций алгоритма. Обозначим через
итераций алгоритма. Обозначим через 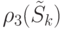 значение диагностического разрешения при диагностировании с помощью этого
значение диагностического разрешения при диагностировании с помощью этого 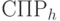 .
.
Очевидно, что последовательность
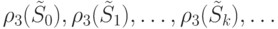
неубывающая. Действительно, на каждой последующей итерации алгоритма 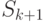 получается из
получается из 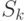 разбиением одного или нескольких блоков на более мелкие блоки. Диагностическое разрешение (отношение количества различимых пар состояний к общему числу пар состояний) от этого может только увеличиться.
разбиением одного или нескольких блоков на более мелкие блоки. Диагностическое разрешение (отношение количества различимых пар состояний к общему числу пар состояний) от этого может только увеличиться.
Более того, можно легко показать, что последовательность
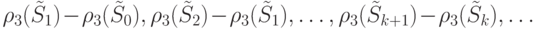
не возрастает.
Из сказанного следует, что
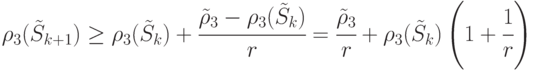
Тогда

Последнее неравенство и доказывает теорему.
Содержательный смысл последней теоремы заключается в том, если маска  заданного объема вычислена с помощью алгоритма 1, то потеря в степени диагностирования с использованием
заданного объема вычислена с помощью алгоритма 1, то потеря в степени диагностирования с использованием 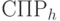 не превосходит 40% от степени диагностирования с
не превосходит 40% от степени диагностирования с  , построенного с помощью оптимальной маски того же объема.
, построенного с помощью оптимальной маски того же объема.
Теперь перейдем к оценке сложности алгоритма 1.
Теорема 4. Вычислительная сложность алгоритма 1 оценивается величиной 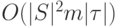 . Объем необходимой для функционирования алгоритма памяти равен
. Объем необходимой для функционирования алгоритма памяти равен 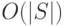 .
.
Доказательство. Оценим сначала вычислительную сложность алгоритма.
Как отмечалось ранее, максимальное количество итераций алгоритма равно 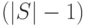 . На каждой итерации производится поиск точки проверки, доставляющей минимум величине (31.9).
Общее количество точек проверки есть
. На каждой итерации производится поиск точки проверки, доставляющей минимум величине (31.9).
Общее количество точек проверки есть  , а для того чтобы подсчитать (31.9) для конкретной точки проверки, необходимо выполнить
, а для того чтобы подсчитать (31.9) для конкретной точки проверки, необходимо выполнить 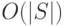 операций для вычисления
операций для вычисления 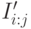 . Таким образом, общее количество операций в алгоритме
. Таким образом, общее количество операций в алгоритме
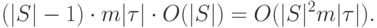
Оценивая емкостную сложность алгоритма заметим, что в ходе его работы необходима память для хранения текущей маски, разбиения 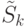 , счетчика итераций
, счетчика итераций  и двух значений
и двух значений 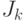 и
и 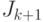 .
Ни одно из значений
.
Ни одно из значений  ,
, 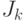 и
и 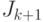 не превышает по величине
не превышает по величине 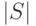 . Суммарное количество элементов в блоках разбиения
. Суммарное количество элементов в блоках разбиения 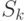 равно
равно 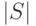 .
Согласно следствию из теоремы 2 объем маски не превышает
.
Согласно следствию из теоремы 2 объем маски не превышает 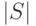 . Отсюда получаем оценку емкостной сложности, приведенную в формулировке теоремы.
. Отсюда получаем оценку емкостной сложности, приведенную в формулировке теоремы.
Экспериментальным данным для оценки эффективности алгоритма 1 и еще одного жадного алгоритма, о котором речь пойдет в следующей лекции, на ДИ, порождаемой реальными устройствами, будет посвящена отдельная лекция.
Ключевые термины:
Жадный алгоритм - алгоритм, основанный на принятии локально оптимальных решений на каждом этапе его работы в расчете на возможность получения глобального оптимума.
Дерево принятия решений - граф, обычно применяемый для решения задач классификации объектов. Он представляет собой дерево,на ребрах которого записаны атрибуты, являющиеся аргументами целевой функции, а в листьях записаны значения этой целевой функции. Во всех прочих вершинах дерева записаны атрибуты, по которым различаются классифицируемые объекты.
Краткие итоги:
В лекции описан жадный алгоритм поиска единой маски ДИ, базирующийся на использовании конструкции дерева принятия решений, призводится оценка объема получаемой маски и вычислительной сложности алгоритма.
Вопросы и упражнения
- Обоснуйте возможность применения алгоритмов решения задач классификациио объектов к задачам поиска масок ДИ.
- Кратко изложите на идейном уровне суть описанного в лекции алгоритма 1 поиска единой маски.
- Поясните, в чем заключается различие алгоритма С4.5 и алгоритма 1, описанного в лекции.
- Приведите верхнюю оценку объема минимальной маски для заданного СПР, получаемой по алгоритму 1.
- Приведите оценки вычислительной сложности алгоритма 1 и объема необходимой для его функционирования памяти.