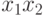|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Анализ состязаний
Явление состязания сигналов
Состязания сигналов в реальных ДУ возникают вследствие того, что смена входных сигналов при подаче следующего набора происходит не одновременно и существует разброс задержек элементов в схеме
[
2.2
]
,
[
1.2
]
. Схема, реализующая булеву функцию  , содержит статическое (динамическое) состязание на переходе между двумя двоичными наборами
, содержит статическое (динамическое) состязание на переходе между двумя двоичными наборами 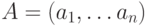 и
и 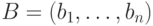 , если
, если 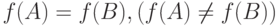 и во время перехода на выходе схемы может возникнуть один или несколько кратковременных импульсов. Статистическое состязание называется
и во время перехода на выходе схемы может возникнуть один или несколько кратковременных импульсов. Статистическое состязание называется  -состязанием, если
-состязанием, если  и
и  -состязанием, если
-состязанием, если  . Динамическое состязание называется
. Динамическое состязание называется 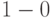 – состязанием, если
– состязанием, если 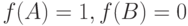 и
и 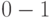 – состязанием, если
– состязанием, если 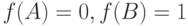 . Как статистические, так и динамические состязания могут быть двух типов: функциональные и логические.
. Как статистические, так и динамические состязания могут быть двух типов: функциональные и логические.
Фукциональные состязания
Рассмотрим пример функционального состязания для булевой функции, представленной на карте Карно (
таблица
6.1). Напомним, что каждая клетка карты соответствует двоичному входному набору. Рассмотрим переход между следующими двоичными наборами  отмеченными на карте Карно
отмеченными на карте Карно  и
и  . Если значение
. Если значение  изменяется раньше чем
изменяется раньше чем  , то на данном переходе возможно кратковременное появление набора
, то на данном переходе возможно кратковременное появление набора 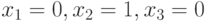 (попадание в клетку
(попадание в клетку 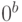 карты Карно). Это вызывает появление на выходе cхемы, реализующей данную булеву функцию, кратковременного
карты Карно). Это вызывает появление на выходе cхемы, реализующей данную булеву функцию, кратковременного  -импульса, то есть происходит статическое
-импульса, то есть происходит статическое  состязание. Аналогично при переходе из клетки
состязание. Аналогично при переходе из клетки  в
в 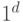 карты Карно происходит динамическое состязание
карты Карно происходит динамическое состязание 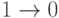 .
.
Определим более точно функциональное статистическое состязание. Булева функция  на переходе
на переходе 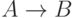 (для определенности пусть изменяются значения первых
(для определенности пусть изменяются значения первых  переменных
переменных  содержит функциональное статистическое состязание
содержит функциональное статистическое состязание  , если среди
, если среди 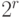 входных наборов с зафиксированными значениями
входных наборов с зафиксированными значениями 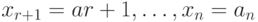 найдутся хотя бы два набора
найдутся хотя бы два набора  и
и  такие, что
такие, что  .
.
Таким образом, функциональное состязание отражает свойства данной булевой функции, а не ее схемной реализации. Очевидно, что на соседних наборах, отличающихся значениями только одной переменной, функционального состязания быть не может. Никакая реализация булевой функции не может устранить функциональное состязание .
Логические состязания
Логические состязания определяются структурой логической схемы, реализующей данную булеву функцию. Рассмотрим это явление на примере функции, представленной на карте Карно рис.6.1 .
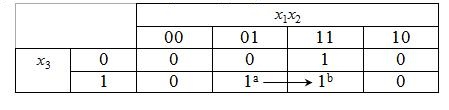
Для перехода 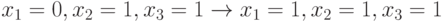 у логической схемы, реализующей данную булеву функцию, которая представлена на рис.6.2 , значения выхода схемы
у логической схемы, реализующей данную булеву функцию, которая представлена на рис.6.2 , значения выхода схемы  одинаковы на начальном и конечном входных наборах этого перехода. Однако, если значение выхода нижнего вентиля
одинаковы на начальном и конечном входных наборах этого перехода. Однако, если значение выхода нижнего вентиля  изменится раньше чем верхнего, то на выходе схемы появится кратковременный нулевой импульс. Таким образом, здесь присутствует статическое логическое состязание .
изменится раньше чем верхнего, то на выходе схемы появится кратковременный нулевой импульс. Таким образом, здесь присутствует статическое логическое состязание .
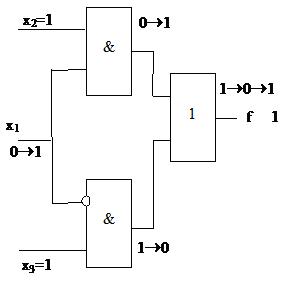
Отметим, что поскольку на этом переходе изменяется значение только одной переменной, то функциональное состязание на нем в принципе невозможно. Кроме этого, данное логическое состязание присуще именно этой схемной реализации. Так, если в схеме рис.6.2 добавить в первом уровне третий элемент конъюнкции (соответствующий третьей простой импликанте данной булевой функции), то состязание в полученной схеме рис.6.3 (реализующей ту же булеву функцию) на рассматриваемом переходе отсутствует.
Определим более строго логическое состязание . Комбинационная схема, реализующая булеву функцию  , содержит статическое логическое состязание на переходе
, содержит статическое логическое состязание на переходе 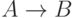 , если на всех
, если на всех 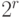 наборах с зафиксированными значениями
наборах с зафиксированными значениями 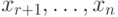 значения функции одинаковы
значения функции одинаковы  , но во время перехода может появиться кратковременный импульс на выходе схемы. Аналогично определяется и динамическое логическое состязание для случая
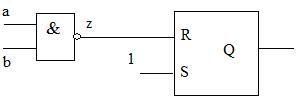
, но во время перехода может появиться кратковременный импульс на выходе схемы. Аналогично определяется и динамическое логическое состязание для случая 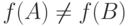 . Известно, что если схема свободна от статистических состязаний, то она свободна и от динамических состязаний. Состязания сигналов особенно опасны для последовательностных схем, потому что могут в них вызвать непредсказуемые переключения элементов памяти. Такая ситуация показана на рис.6.4 , где состязание на выходе вентиля
. Известно, что если схема свободна от статистических состязаний, то она свободна и от динамических состязаний. Состязания сигналов особенно опасны для последовательностных схем, потому что могут в них вызвать непредсказуемые переключения элементов памяти. Такая ситуация показана на рис.6.4 , где состязание на выходе вентиля  может привести к установке триггера в неправильное (и непредсказуемое) состояние. Разработана и более тонкая классификация состязаний (особенно для последовательностных схем) [48].
может привести к установке триггера в неправильное (и непредсказуемое) состояние. Разработана и более тонкая классификация состязаний (особенно для последовательностных схем) [48].