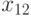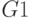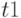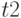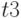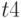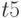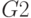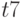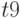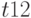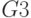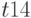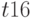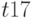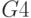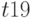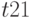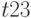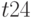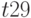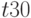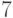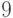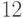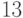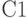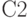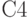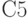|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Многомерная активизация путей в шестизначном алфавите
18.2 D - алгоритм
Среди структурных методов генерации тестов, использующих многозначные алфавиты, первым был разработан D-алгоритм [18.3], который позволяет выполнять многомерную активизацию путей и гарантирует построение проверяющего теста для неизбыточной неисправности в комбинационной схеме.
Основным рабочим инструментом в D-алгоритме является техника кубов. Модели логических элементов представляются также с помощью кубов. Например, в табл. 18.5 представлены 0-кубы для вентиля И. Легко видеть, что данная таблица в сжатой форме содержит все условия, при которых на выходе вентиля И возможно значение 0. Можно показать, что множество сжатых кубов, используемое в D-алгоритме, определяется соответствующей функцией 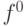 .
Так, например, каждый терм функции
.
Так, например, каждый терм функции 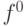 вентиля соответствует строке табл. 18.5. Аналогично функция
вентиля соответствует строке табл. 18.5. Аналогично функция 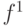 соответствует табл. 18.6, которая содержит 1-кубы и определяет условия, при которых на выходе вентиля И возможна 1.
соответствует табл. 18.6, которая содержит 1-кубы и определяет условия, при которых на выходе вентиля И возможна 1.
Распространение символов 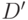 и
и  через логические элементы осуществляется с помощью
через логические элементы осуществляется с помощью 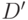 - и
- и  -кубов, которые определяются функциями многозначными функциями
-кубов, которые определяются функциями многозначными функциями
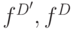 соответственно.
Так, табл. 18.7, содержащая
соответственно.
Так, табл. 18.7, содержащая  -кубы вентиля И, получена из функции
-кубы вентиля И, получена из функции  вентиля И. Аналогично, функция
вентиля И. Аналогично, функция 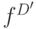 определяет
определяет 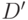 -кубы табл. 18.8.
-кубы табл. 18.8.
Простым кубом неисправности  на выходе вентиля называется
на выходе вентиля называется  (
(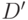 )-куб (
)-куб ( для неисправности
для неисправности  ,
, 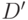 для неисправности
для неисправности 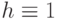 ), в котором выходу вентиля присваивается
), в котором выходу вентиля присваивается  (
(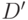 ), а значения входам присваиваются таким образом, чтобы на выходе исправного вентиля было значение, инверсное
), а значения входам присваиваются таким образом, чтобы на выходе исправного вентиля было значение, инверсное  . Например,
. Например,  является простым
является простым  -кубом для неисправности
-кубом для неисправности  на входе вентиля И. Очевидно, что простой
на входе вентиля И. Очевидно, что простой  -куб служит средством активизации неисправности на соответствующей линии схемы (он вносит влияние неисправности в месте ее возникновения).
-куб служит средством активизации неисправности на соответствующей линии схемы (он вносит влияние неисправности в месте ее возникновения).
Основной моделью логической схемы в  -алгоритме является система таблиц кубов, в которых столбцы соответствуют линиям схемы, а строки - кубам. Например, табл. 18.9 содержит
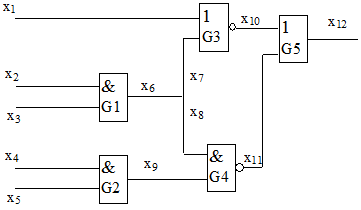
-алгоритме является система таблиц кубов, в которых столбцы соответствуют линиям схемы, а строки - кубам. Например, табл. 18.9 содержит 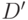 кубы для схемы, изображенной на рис. 18.4. Пустые клеточки соответствуют неопределенным значениям
кубы для схемы, изображенной на рис. 18.4. Пустые клеточки соответствуют неопределенным значениям  . Вторая таблица содержит 0(1)-кубы. Для нашего примера она представлена в табл. 18.10.
. Вторая таблица содержит 0(1)-кубы. Для нашего примера она представлена в табл. 18.10.
Кроме этих таблиц используется куб  для текущих значений линий схемы и несколько стеков. Сначала всем линиям в кубе
для текущих значений линий схемы и несколько стеков. Сначала всем линиям в кубе  присваиваются неопределенные значения
присваиваются неопределенные значения  . Затем в
. Затем в  вносится простой куб данной неисправности. Далее выполняется
вносится простой куб данной неисправности. Далее выполняется  -распространение к одному из выходов схемы. Оно выполняется путем выбора последователя неисправного вентиля и пересечения с одним из его
-распространение к одному из выходов схемы. Оно выполняется путем выбора последователя неисправного вентиля и пересечения с одним из его  -кубов с текущим кубом
-кубов с текущим кубом  .
При
.
При  -распространении обычно производится выбор
-распространении обычно производится выбор  или
или 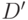 -куба данного элемента, оставшиеся варианты хранятся в стеке. Операция пересечения определена в табл. 18.11. Если при пересечении кубов, возникает хотя бы один символ
-куба данного элемента, оставшиеся варианты хранятся в стеке. Операция пересечения определена в табл. 18.11. Если при пересечении кубов, возникает хотя бы один символ  , то это показывает противоречие, возникающее на данной линии вследствие различных требований (например, из простого
, то это показывает противоречие, возникающее на данной линии вследствие различных требований (например, из простого  -куба следует, что данная линия должна иметь значение 0, а из условий
-куба следует, что данная линия должна иметь значение 0, а из условий  распространения здесь должна быть 1.
распространения здесь должна быть 1.
 -алгоритм можно сформулировать следующим образом в виде псевдокода.
-алгоритм можно сформулировать следующим образом в виде псевдокода.
D-алгоритм( неисправность h_{i})
{
Ранжирование элементов схемы от входов к выходам;
Выбор простого D-куба для неисправности h_{i};
Занесение элементов-последователей h_{i} в D-границу;
D-распространение();
Доопределение();
Return();
}
D-распространение()
//активизирует пути с D,D'-значениями от неисправности до внешнего выхода
{
while(есть необработанные элементы в D-границе)
{
Выбор следующего необработанного элемента из D-границы;
while(есть необработанные последователи элемента)
{
Выбор следующего элемента-последователя;
Выбор D-куба для элемента-последователя;
D-пересечение выбранного D-куба с текущим тест-кубом К;
if(пересечение пусто или неопределено)continue;
//переход на конец цикла
if(все D-кубы элемента использовались и не дали результата) break;
if(пересечение D-кубов успешно)
{
Занесение элементов-последователей D-значений в D-границу;
Сохранение состояния алгоритма в стеки;
break;
}
else if (пересечение D-куба с тестовым кубом пусто) возврат();
else if ( противоречие при операции пересечения кубов) break;
}
if(ни один из вариантов не дал D-распространения)
Возврат();
}
return;
}
Доопределение()
//дает значения внешних входов, обеспечивающие условия D-распространения
{
J=координаты тестового куба К с определенными значениями 0,1 ;
if(J содержит только внешние входы)
тест построен, останов;
for(каждого неподтвержденного сигнала в G)
{
выбор 0,1 сигнала z из J с наибольшим рангом;
if(входы элемента с выходом z все равны D или D')
break;
while(есть необработанные 0,1-кубы вентиля z)
{
Выбор следующего необработанного 1- или 0- куба вентиля z;
if(нет необработаных 1- или 0- кубов)
{
if(нет выбора в стеке импликации) stop;
неисправность избыточна;
else if(есть альтернативный выбор)
then извлечение из стека альтернативного значения;
else
{
Возврат();
D-распространение();
}
}
if(0,1-куб пересекается с z) удаление z из J и занесение в J-границу значений входов z;
break;
if(пересечение пусто) отметка текущего 0,1-куба как отработанного;
}
}
return;
}
Возврат()
{
if( внешний выход содержится в D-границе)
Доопределение();
else if(извлечение из стека импликации альтернативного значения);
if(нет вариантов в стеке импликации) stop;
неисправность избыточна;
else return;
}
D-алгоритм