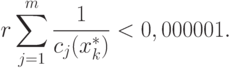Лекция 13: Решение задач нелинейного программирования с ограничениями. Геометрическая интерпретация задач нелинейного программирования
2. Метод SUMT Фиакко и Маккормика
Результаты предыдущего раздела показывают, что можно решить
задачу минимизации с ограничениями (минимизировать функцию f(х) при ограничениях 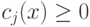 , решая для последовательности значений r, стремящейся к нулю, задач без ограничений
следующего вида:
, решая для последовательности значений r, стремящейся к нулю, задач без ограничений
следующего вида:
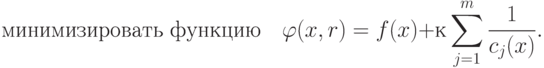
Метод SUMT
(sequential unconstrained minimisation technique)
был впервые предложен Кэрролом в 1961 году. Его идеи были исследованы
Фиакко и Маккормиком, которые не только рассмотрели теоретические
вопросы и сходимость метода, но создали практическую систему для его
реализации. Редко можно будет использовать данный метод так, как это
делалось в двух примерах из предыдущего раздела, поскольку далеко не
всегда можно найти оптимальную точку для функций 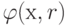 в виде функции х*(r),
предел которой при
в виде функции х*(r),
предел которой при 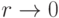 можно исследовать.
можно исследовать.
Поэтому для того, чтобы можно было применить настоящий метод на
практике, необходимо построить вычислительный метод, использующий
теоретическое свойство сходимости, рассмотренное в предыдущем разделе.
Теоретически здесь не возникает трудностей. Для заданных функцией f(х) ограничениях 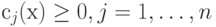 ,
необходимо выбрать начальное значение r = r0,
чтобы сформировать функцию
,
необходимо выбрать начальное значение r = r0,
чтобы сформировать функцию  , которая
минимизируется без ограничений методом ДФП. Найдя минимум функции
, которая
минимизируется без ограничений методом ДФП. Найдя минимум функции  , необходимо уменьшить значение r. Это можно сделать эффективно и просто, если найти r1 = r0/c, где константа с > 1. Затем необходимо минимизировать функцию
, необходимо уменьшить значение r. Это можно сделать эффективно и просто, если найти r1 = r0/c, где константа с > 1. Затем необходимо минимизировать функцию  , снова используя метод ДФП. Таким
образом, будет разработана итерационная процедура.
На k -м шаге минимизируется функция
, снова используя метод ДФП. Таким
образом, будет разработана итерационная процедура.
На k -м шаге минимизируется функция  , минимум которой находится в точке
, минимум которой находится в точке 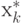 . Важно, что ее можно использовать в дальнейшем
в качестве первой точки в итерационной процедуре минимизации функции
. Важно, что ее можно использовать в дальнейшем
в качестве первой точки в итерационной процедуре минимизации функции 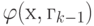 , где rk+1 = гk/с. Теперь ясно, что
последовательность rk убывает и стремится к
нулю, следовательно, последовательность точек минимумов будет
сходиться к решению задачи с ограничениями.
, где rk+1 = гk/с. Теперь ясно, что
последовательность rk убывает и стремится к
нулю, следовательно, последовательность точек минимумов будет
сходиться к решению задачи с ограничениями.
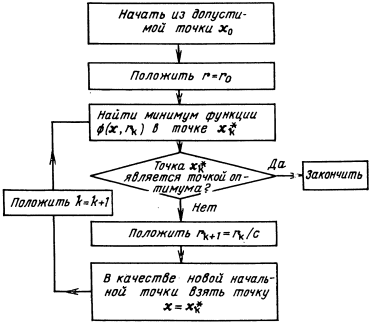
Ниже приведена блок-схема (рис. 13.1) метода SUMT. Остается уточнить некоторые детали.
Предполагается, что в начале процедуры имеется допустимая точка.
Важно, чтобы в процессе последующих вычислений получаемые точки
принадлежали допустимой области.
Метод ДФП является градиентным
методом минимизации, использующим при одномерном поиске кубическую
интерполяцию. Тогда, по мере приближения точки x к
границе внутри допустимой области 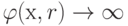 , а по мере
приближения точки x к границе снаружи допустимой
области
, а по мере
приближения точки x к границе снаружи допустимой
области 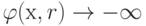 .
.
Таким образом, если поиск осуществляется вдоль прямой, соединяющей две точки, одна из которых лежит внутри, а другая вне области ограничений, то кубическая интерполяция оказывается неприемлемой, поскольку функция разрывна вдоль данной прямой. Действительно, если минимум будет найден вне допустимой области, то метод ДФП не позволит вновь войти в область ограничений. Необходимо тщательно исследовать такие вопросы при использовании метода ДФП в данной задаче.
Выбор начального значения r может оказаться важным
с точки зрения сокращения числа итераций при минимизации функции 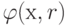 . Если сначала r выбрано очень
малым, для того чтобы функция
. Если сначала r выбрано очень
малым, для того чтобы функция 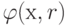 мало
отличалась от функции f(x), то метод будет сходиться
очень быстро. Однако такой выбор может привести к серьезным
осложнениям при вычислениях. Для малых r функция
мало
отличалась от функции f(x), то метод будет сходиться
очень быстро. Однако такой выбор может привести к серьезным
осложнениям при вычислениях. Для малых r функция 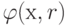 будет быстро меняться в окрестности
минимума, что может вызвать затруднения при использовании градиентного
метода. Слишком же большое значение r может привести к
тому, что штрафная функция Р(х) в уравнении (1.4) станет
доминирующей. Поэтому "разумный" выбор начальной точки очень
важен. Для многих задач "разумным" значением для начальной
точки является значение r0 = 1. Более
рациональный подход состоит в том, чтобы понять, что если начальная
точка x будет лежать вблизи минимума функции
будет быстро меняться в окрестности
минимума, что может вызвать затруднения при использовании градиентного
метода. Слишком же большое значение r может привести к
тому, что штрафная функция Р(х) в уравнении (1.4) станет
доминирующей. Поэтому "разумный" выбор начальной точки очень
важен. Для многих задач "разумным" значением для начальной
точки является значение r0 = 1. Более
рациональный подход состоит в том, чтобы понять, что если начальная
точка x будет лежать вблизи минимума функции
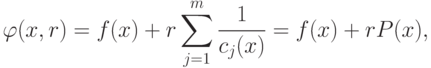
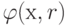 будет мал:
будет мал: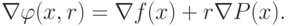 |
( 2.1) |
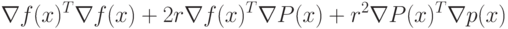 |
( 2.2) |
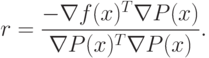 |
( 2.3) |
Это начальное значение r, как предполагает Фиакко и Маккормик, должно давать хорошие результаты в общем случае. Уменьшить значение r очень простo: rk+1 = rk/с, где с = 10.
Для минимизации функции 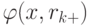 используется метод ДФП. В качестве начальной точки используется
оптимальная точка функции
используется метод ДФП. В качестве начальной точки используется
оптимальная точка функции 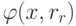 , и это
оказывается очень эффективным. Oднако необходимо обратить внимание
на то, чтобы в процессе одномерного поиска не выйти за область
ограничений. Грубым, но вполне эффективным является следующий
метод. Пусть имеются точка p и направление поиска d=-Hg. Следующая точка
, и это
оказывается очень эффективным. Oднако необходимо обратить внимание
на то, чтобы в процессе одномерного поиска не выйти за область
ограничений. Грубым, но вполне эффективным является следующий
метод. Пусть имеются точка p и направление поиска d=-Hg. Следующая точка 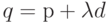 необходима для осуществления
кубической интерполяции. Начнем со значения
необходима для осуществления
кубической интерполяции. Начнем со значения 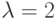 (удвоенный шаг в методе Ньютона) и
проверим, является ли точка q допустимой, т.е.
выполняется ли неравенство сj(q) > 0
для всех j. Если оно выполняется, то
(удвоенный шаг в методе Ньютона) и
проверим, является ли точка q допустимой, т.е.
выполняется ли неравенство сj(q) > 0
для всех j. Если оно выполняется, то  не меняется, но если неравенство не
выполняется, то
не меняется, но если неравенство не
выполняется, то  заменяется на
заменяется на  находится новая точка q и вновь производится проверка. В конце концов
допустимая точка q будет найдена, и тогда можно
осуществить интерполяцию. Выбор значения
находится новая точка q и вновь производится проверка. В конце концов
допустимая точка q будет найдена, и тогда можно
осуществить интерполяцию. Выбор значения  не вполне очевиден. Выбор
не вполне очевиден. Выбор 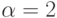 был успешным,
при
был успешным,
при  длина шага становится близкой к
расстоянию до ближайшей границы области ограничений и поэтому
является "безопасной" для интерполяционной процедуры.
длина шага становится близкой к
расстоянию до ближайшей границы области ограничений и поэтому
является "безопасной" для интерполяционной процедуры.
Важно не дать точкам выйти за область ограничений в процессе минимизации.
Функция  минимизируется до тех пор,
пока два последовательных значения F1 и F2 не станут такими, что |(F1–F2)/F1|<0,000001.
Это условие, конечно, может быть изменено. В соответствии с
соотношением (1.17) процесс минимизации заканчивается, когда
минимизируется до тех пор,
пока два последовательных значения F1 и F2 не станут такими, что |(F1–F2)/F1|<0,000001.
Это условие, конечно, может быть изменено. В соответствии с
соотношением (1.17) процесс минимизации заканчивается, когда