Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать программу

Лекция 5: Двойственность в линейном программировании. Нахождение допустимых базисных решений. Двойственная задача линейного программирования, ее структура и свойства. Общий случай двойственности.

A

|

версия для печати

2.2. Общий случай двойственности

В предыдущем разделе были установлены основные соотношения для пары двойственных задач ЛП при ограничениях в форме неравенств. Обобщим эти результаты на случай произвольных ограничений.

Пусть прямая задача ЛП задана в виде

$\text{максимизировать} \; \sum_{j=1}^n c_j x_j$

( 2.2.1)

при условиях

$\sum_{j=1}^n a_{ij} x_j \leq b_i , \; i=1,2,\ldots,m_1 \leq m ;$

( 2.2.2)

$\sum_{j=1}^n a_{ij} x_j = b_i , \; i = m_1 + 1, m_1 + 2, \ldots, m ;$

( 2.2.3)

$x_j \geq 0, \; j = 1,2,\ldots,n_1 \leq n.$

Тогда двойственная задача по отношению к задаче (2.2.1)-(2.2.3) записывается так:

$\text{минимизировать} \; \sum_{i=1}^m b_i y_i$

( 2.2.4)

при условиях

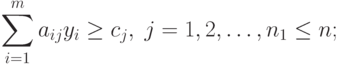$\sum_{i=1}^m a_{ij} y_i \geq c_j, \; j = 1,2,\ldots, n_1 \leq n ;$

( 2.2.5)

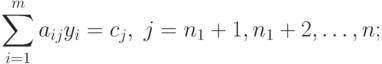$\sum_{i=1}^m a_{ij} y_i = c_j, \; j = n_1+1,n_1+2,\ldots, n ;$

( 2.2.6)

Таким образом, задача, двойственная к задаче со смешанными ограничениями (неравенства-равенства), составляется согласно следующим правилам.

Если переменная x_j прямой задачи предполагается неотрицательной, то j -е условие системы (2.2.5) является неравенством.
Если на переменную x_j не накладывается ограничение на знак, то j -е ограничение двойственной задачи (2.2.5) будет равенством.

Аналогично связаны знаки переменных двойственной задачи y_i и соответствующие им ограничения прямой задачи.

Заметим, что если положить m₁=m и n₁=n, то получим частный случай пары двойственных задач с ограничениями в форме неравенств.

Докажем справедливость соотношений (2.2.1) - (2.2.3) и (2.2.4) - (2.2.6), связывающих прямую и двойственную задачи.

Свяжем с каждой ЛП - задачей вида (2.2.1) - (2.2.3) следующую задачу с ограничениями в форме неравенств:

$\text{максимизировать} \; \sum_{j=1}^{n_1} c_j x'_j + \sum_{j=n_1 +1}^n c_j (x'_j - x'_{j+n_1})$

( 2.2.7)

при условиях

$\sum_{j=1}^{n_1} a_{ij} x'_j + \sum_{j=n_1 + 1}^n a_{ij} (x'_j - x'_j+n_2) \leq b_i; \; i=1,2,\ldots,m ;$

( 2.2.8)

$- \sum_{j=1}^{n_1} a_{ij} x'_j + \sum_{j=n_1 + 1}^n a_{ij} (x'_j - x'_j+n_1) \leq -b_i; \; i=m_1+1,m_1+2,\ldots,m ;$

( 2.2.9)

$x'_j \geq 0; \; j=1,2,\ldots,n+n_2,$

( 2.2.10)

где n₂=n-n₁ - число переменных задачи (2.2.1) - (2.2.3), на которые не наложено условие неотрицательности.

Установим соответствие между переменными задач (2.2.1) - (2.2.3) и (2.2.7) - (2.2.10). Сравнивая формы их записи, убеждаемся, что n -мерный вектор х={x₁,.,x_n} и (n+n₂) -мерный вектор $x' = \{ x'_1, x'_2, .,x'_{n+n_2} \}$ связаны соотношением

$x_j = \left\{ \begin{aligned} & x'_j, \; j=1,2,\ldots,n_1 \\ & x'_j - x'_{j+n_2}, \; j=n_1 + 1, n_1 + 2, \ldots, n \end{aligned} \right.$

( 2.2.11)

Очевидно, каждому (n+n₂) -мерному вектору x' соответствует единственный n -мерный вектор x, и вместе с тем произвольному n -мерному вектору x соответствует целое семейство (n+n₂) -мерных векторов х'.

Таким образом, соответствие, устанавливаемое формулой (2.2.11), является однозначным только в одну сторону.

Вместе с тем среди семейства векторов х', соответствующих x, всегда существуют векторы с неотрицательными компонентами.

Пусть вектор $x'= \{ x'_1, x'_2, ., x'_{n+n_2} \}$ - план задачи (2.2.7) -(2.2.10). Используя соотношение (2.2.11), можно легко получить, что соответствующий вектор x является планом задачи. И наоборот, если x - план задачи (2.2.1) - (2.2.3), то существует целое семейство планов x' задачи (2.4.38) - (2.4.41), среди которых имеются заведомо неотрицательные.

Одним из них является вектор ${\widetilde{x}}\,'$ где

j = 1, 2, ., n₁,
j = n₁+1, n₁+2, ., n,
j = n+1, n+2, ., n+n₂.

${\widetilde{x}}\,'_j = \left\{ \begin{aligned} & x_j \\ & \max (0, x_j) , \\ & \max (0, -x_{j-n_2}) , \end{aligned} \right.$

( 2.2.12)

Неотрицательность всех компонентов ${\widetilde{x}}\,'$ очевидна, а соответствие векторов x и ${\widetilde{x}}\,'$ следует из равенства

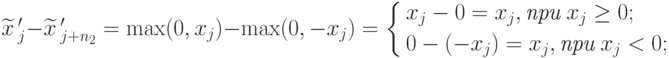
${\widetilde{x}}\,'_j - {\widetilde{x}}\,'_{j+n_2} = \max (0, x_j) - \max (0, -x_j) = \left\{ \begin{aligned} & x_j - 0 = x_j, \textit{при} \; x_j \geq 0; \\ & 0 - (-x_j) = x_j , \textit{при} \; x_j < 0; \end{aligned} \right.$

где j=n₁+1; n₁+2,.,n...

Рассмотрим задачу (2.2.4) - (2.2.6), двойственную к задаче (2.2.1) - (2.2.3). Нетрудно показать, что она приводится к виду (2.2.1) - (2.2.3). Для этого достаточно положить $\overline{c}_j = -c_j ; \; \overline{a}_{ij} = -a_{ij} ; \; \overline{b}_i = -b_i$ . При этом задача (2.2.4) - (2.2.6) переходит в задачу

$\text{минимизировать} \; \sum_{i=1}^m \overline{b}_i y_i$

( 2.2.13)

при условиях

$\sum_{i=1}^m \overline{a}_{ij} y_i \geq \overline{c}_j, \; j=1,2,.,n_1 ;$

( 2.2.14)

$\sum_{i=1}^m \overline{a}_{ij} y_i = \overline{c}_j, \; j=n_1+1, n_1+2,.,n ;$

( 2.2.15)

$y_i \ge 0; \; i=1,2,.,m_1.$

( 2.2.16)

Поэтому задаче (2.2.4) - (2.2.6) соответствует следующая задача с ограничениями в форме неравенств:

$\text{минимизировать} \; \sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1 + 1}^m b_i (y'_i - y'_{i+m_1})$

( 2.2.17)

при условиях

$\sum^m_{i=1} \overline b_{ij}y_{ij}\ge \overline c_j \ j= 1,2 \ldots,n;$

( 2.2.18)

$- \sum_{i=1}^{m_1} a_{ij} y'_i - \sum_{i=m_1+1}^m a_{ij}(y'_i - y'_{i+m_1}) \geq -c_j ; \; j=n_1+1; n_1+2,.,n.$

( 2.2.19)

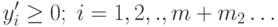$y'_i \geq 0; \; i=1,2,.,m+m_2 \ldots$

( 2.2.20)

где m₂ = m - m₁ - число переменных y_i, на которые не наложено условие неотрицательности.

Вектор y={y₁,.,y_m} и соответствующий ему (m+m₂) мерный вектор $y' = \{ y'_1,.,y'_{m+m_2} \}$ связанны соотношением

$y_i = \left \{ \begin{aligned} & y'_i, \; i=1,2,\ldots,m_1 ; \\ & y'_i - y'_{i+m_1}, \; i=m_1 +1, m_1+2,\ldots,m. \end{aligned} \right.$

( 2.2.21)

Следовательно, каждому плану y' задачи (2.2.17) - (2.2.20) соответствует план у задачи (2.2.4) - (2.2.6), и наоборот: любой неотрицательный вектор, соответствующий плану (решению) задачи (2.2.4) - (2.2.6), является решением задачи (2.2.18) - (2.2.20). При этом, если у' и у - два соответствующих друг другу решения, то из оптимальности одного из них непосредственно следует оптимальность другого.

Запишем задачу, двойственную к (2.2.7) - (2.2.10). Непосредственной проверкой можно убедиться в том, что получим задачу в форме (2.2.17) - (2.2.20). Таким образом, задачи (2.2.7) - (2.2.10) и (2.2.17) -(2.2.20) с произвольными ограничениями (неравенства - равенства) также представляют собой двойственную пару.

Заметим, что все теоремы двойственности, доказанные для задач с ограничениями в форме неравенств, легко распространяются на общий случай задач с произвольными ограничениями.

Рассмотрим для примера теорему 2.2.1.

Если х и у - допустимые решения прямой (2.2.1) - (2.2.2) и двойственной (2.2.4) - (2.2.6) задачи и если при этом $\sum_{j=1}^n c_j x_j = \sum_{i=1}^m b_i y_i$ , то х и у - оптимальные решения этих задач.

Доказательство. Допустим, что задача (2.2.1) - (2.2.2) разрешима и x -ее допустимое решение, а у - допустимое решение (план) задачи (2.2.4) - (2.2.6). Рассмотрим вектор 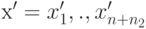$х'={x'_1,.,x'_{n+n_2}}$ , связанный с вектором х соотношениями (2.2.11), с неотрицательными компонентами. По доказанному выше х' является решением задачи (2.2.7).

Воспользуемся тогда теоремой 2.2.1 для задач с ограничениями - неравенствами.

Согласно этой теореме, если х' и у' - допустимые решения пары двойственных задач и выполняется равенство

$\sum_{j=1}^{n_1} c_j x'_j + \sum_{j=n_1+1}^n c_j (x'_j - x'_{j+n_2}) = \sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1+1}^m b_i (y'_i - y'_{i+m_2})$

( 2.2.22)

то х' и у' - оптимальные решения этой пары задач.

Используя соотношения (2.2.11), (2.2.21), связывающие соответствующие планы х' и х, у и у', получим

$\sum_{i=1}^{n_1} c_j x'_j + \sum_{j=n_1+1}^n c_j (x'_j - x'_{j+n_2}) = \sum_{j=1}^{n} c_j x_j ;$

( 2.2.23)

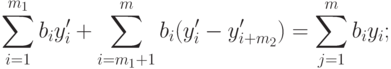$\sum_{i=1}^{m_1} b_i y'_i + \sum_{i=m_1+1}^m b_i (y'_i - y'_{i+m_2}) = \sum_{j=1}^{m} b_i y_i ;$

( 2.2.24)

Таким образом, соотношения (2.2.22) и (2.2.23) - (2.2.24) - эквивалентны, поэтому планы х' и у' - оптимальны.

Но по доказанному выше каждому оптимальному х' соответствует единственный оптимальный план х, а каждому оптимальному плану у' соответствует единственный план у. Теорема доказана.

Аналогичным образом могут быть доказаны остальные теоремы двойственности для произвольных ограничений.

Дальше >>

Введение в математическое программирование

2.2. Общий случай двойственности

Вопросы и ответы

Авторизоваться

Введение в математическое программирование

2.2. Общий случай двойственности

Вопросы и ответы