Лекция 3: Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом
3. Постановка задач линейного программирования и исследование их структуры
Большинство задач, решаемых методами исследования операций, может быть сформулировано так:
максимизировать F(x1, x2, ., xn) при ограничениях
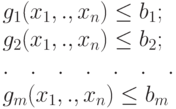
Среди разных разделов математического программирования наиболее развитым и законченным является линейное программирование (ЛП).
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.
Рассмотрим некоторые из них.
Определение оптимального ассортимента. Имеются m видов ресурсов в количествах b1, b2, . , bi, bm и n видов изделий. Задана матрица A=||aij||, i=1 ,.,m, j=1,.,n, где aij характеризует нормы расхода i -го ресурса на единицу j -го вида изделий. Эффективность производства j -го вида изделий характеризуется показателем Cj, удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.
Обозначим количество единиц k -го вида изделий, выпускаемых
предприятием, через xk, 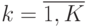 .
Тогда математическая модель этой задачи будет иметь такой вид:
.
Тогда математическая модель этой задачи будет иметь такой вид:
 |
( 3.1) |
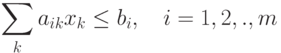 |
( 3.2) |
Кроме ограничений на ресурсы (3.2) в эту модель можно ввести дополнительные
ограничения на планируемый уровень выпуска продукции  , xi : xj : xk = bi : bj : bk
для всех i, j, k и т.д.
, xi : xj : xk = bi : bj : bk
для всех i, j, k и т.д.
Оптимальное распределение взаимозаменяемых ресурсов.
Имеются m видов взаимозаменяемых ресурсов а1, а2, ., аm,
используемых при выполнении n различных работ (задач).
Объемы работ, которые должны быть выполнены, составляют b1, b2, . , bi, bn
единиц. Заданы числа 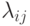 , указывающие, сколько
единиц j -й работы можно получить из единицы і -го
ресурса, а также Cij - затраты на производство j -й работы из единицы i -го ресурса. Требуется
распределить ресурсы по работам таким образом, чтобы суммарная
эффективность выполненных работ была максимальной (или суммарные
затраты - минимальными).
, указывающие, сколько
единиц j -й работы можно получить из единицы і -го
ресурса, а также Cij - затраты на производство j -й работы из единицы i -го ресурса. Требуется
распределить ресурсы по работам таким образом, чтобы суммарная
эффективность выполненных работ была максимальной (или суммарные
затраты - минимальными).
Данная задача называется общей распределительной задачей. Количество единиц i -го ресурса, которое выделено на выполнение работ j -го вида, обозначим через xij.
Математическая модель рассматриваемой задачи такова:
 |
( 3.3) |
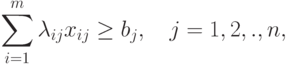 |
( 3.4) |
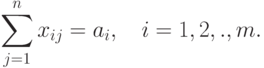 |
( 3.5) |
Ограничение (3.4) означает, что план всех работ должен быть выполнен полностью, а (3.5) означает, что ресурсы должны быть израсходованы целиком.
Примером этой задачи может быть задача о распределении самолетов по авиалиниям.
Задача о смесях. Имеется р компонентов, при сочетании которых в разных пропорциях получают разные смеси. Каждый компонент, а следовательно и смесь, содержит q веществ. Количество k -го вещества k = 1, 2, ., q, входящее в состав единицы і -го компонента и в состав единицы смеси, обозначим через аik и аk соответственно.
Предположим, что аk зависит от аik линейно, то есть если смесь состоит из x1 единиц первого компонента, x2 - единицу второго компонента и т.д., то
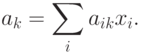
Задано р величин Ci, характеризующих стоимость, массу или калорийность единицы i -го компонента, и q величин bk, указывающих минимально необходимое процентное содержание k -го вещества в смеси. Обозначим через x1, x2,.,xр значение компонента р -го вида, входящего в состав смеси.
Математическая модель этой задачи имеет такой вид:
 |
( 3.6) |
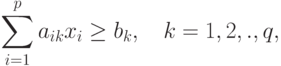 |
( 3.7) |
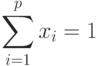
Ограничение (3.7) означает, что процентное содержание k -го вещества в единице смеси должно быть не меньше bk.
К этой же модели принадлежит также задача определения оптимального рациона кормления скота.
