Интерполяция функций
6.5. Теорема об остаточном члене интерполяции
Введем понятие остаточного члена интерполяции для оценки погрешности
 |
( 6.1) |
Теорема. Пусть функция f(t) имеет на отрезке [a, b] — N + 1 ограниченную производную. Тогда
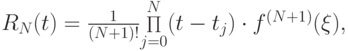
![\xi \in \left[{a, b}\right] $.](/sites/default/files/tex_cache/a1804bb3e997026d294e332ee9b9b628.png)
Доказательство.
Рассмотрим функцию
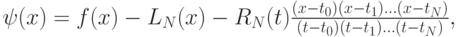
имеющую, по крайней мере, N + 1 производную. По условию, эту производную имеет f(x), а два остальных члена — полиномы.
Кроме того,  на [a, b] имеет, по крайней мере, N + 2 нуля.
на [a, b] имеет, по крайней мере, N + 2 нуля.
Их можно указать. Точки x = tn (n = 0, …, N) — нули, поскольку f(tn) = L(tn), а последнее слагаемое обращается в них в нуль. N + 2 нулем является точка x = t в силу определения остаточного члена. Далее, поскольку между каждыми двумя нулями непрерывно дифференцируемой функции имеется хотя бы один нуль ее производной, на [a, b] имеется хотя бы N + 1 нуль 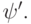 Применяя это рассуждение к
Применяя это рассуждение к  можно показать, что существует точка
можно показать, что существует точка ![\xi \in [a, b]](/sites/default/files/tex_cache/a2d18d95d8e1dd0513eb234c190de1d1.png) такая, что
такая, что 
Вычислим N + 1 производную правой части выражения для f(x) с учетом того, что L(N + 1) = 0. Кроме того, в точке 
![\begin{gather*}
{\psi}^{(N + 1)} (\xi ) = f^{(N + 1)} (\xi ) - L^{(N + 1)} (\xi ) - \frac{d^{N + 1}}{dx^{N + 1}}\left[{R_N (t) \cdot \frac{(x - t_0 ) \ldots (x - t_N)}{(t - t_0 ) \ldots (t - t_N)}}\right]_\xi, \\
L^{(N + 1)} (\xi ) = 0; {\psi}^{(N + 1)} (\xi ) = 0; \\
\frac{d^{N + 1}}{dx^{N + 1}} \left. \left[\frac{(x - t_0 ) \ldots (x - t_N)}{(t - t_N) \ldots (t - t_N)}\right]\right|_{x = \xi} = \frac {(N + 1)!}{\mathop \Pi\limits_{j = 0}^N (t - t_j)} \end{gather*}](/sites/default/files/tex_cache/d5daee788bd15457a2f4cdeedcbe3a1a.png)
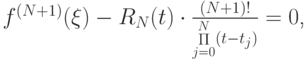
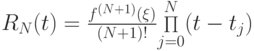
Рассмотрим некоторые важные следствия этой теоремы.
Следствие (точность интерполяции на равномерной сетке).
Положим, что ![t_n = n\tau, \tau = (b - a)/N, t \in \left[{a, b}\right],](/sites/default/files/tex_cache/2d50cf16ad7e0cf7af8d62da27445ede.png) — сетка равномерная. В этом случае имеет место оценка
— сетка равномерная. В этом случае имеет место оценка
![$ \left|{R_N (t)}\right| \le \frac{{\tau ^{N + 1}}}{{N + 1}}C,
C = \max\limits_{t \in \left[{a, b}\right]} \left|{f^{(N + 1)}(t)}
\right|. $](/sites/default/files/tex_cache/547f8e215d842d36166c95bf6d9d16b0.png)
Доказательство. Пусть ![t = t_k + \alpha \tau , \alpha \in \left[{0, 1}
\right], k = 0, 1, \ldots , N - 1.](/sites/default/files/tex_cache/34e80628bfa02b55ceaa9fde6649fe8c.png)
Тогда 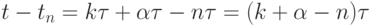 ; откуда
; откуда 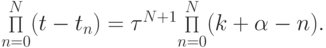 Можно показать, что
Можно показать, что 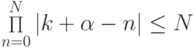 ! . Остаточный член оценивается следующим образом:
! . Остаточный член оценивается следующим образом:

![$ \left|R_N(t)\right| \le \frac {\tau^{N + 1}}{N + 1} \max\limits_{\xi \in \left[{a, b}\right]} \left|{f^{(N + 1)} (\xi)}\right|. $](/sites/default/files/tex_cache/c44948dcb52c5fadb50f2182ef54d38e.png)
Рассмотрим, как ведет себя оценка в задаче экстраполяции при удалении точки t от интервала [t0, tN]. При ![t \in \left[{t_N , t_N + \tau }\right]](/sites/default/files/tex_cache/f8c670cbbc9258eabec9d5245da89fc8.png) имеем
имеем ![\left|{R_N (t)}\right| \le \tau ^{N + 1} \cdot \max\limits_{\xi \in [t_0, t_N + \tau ]} \left|{f^{(N + 1)} (\xi )}\right|,](/sites/default/files/tex_cache/5093249d7ff8f7d00083787294d36a4e.png) поскольку
поскольку 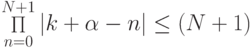 !. При
!. При
![t \in \left[{t_N + \tau , t_N + 2\tau }\right] \left|{R_N (t)}\right| \le (N + 2) \tau ^{N + 1} \cdot \max\limits_{\xi \in [t_0, t_N + 2\tau ]} \left|{f^{(N + 1)} (\xi )}\right|,](/sites/default/files/tex_cache/2df2c89262514ee9e288df217622ab61.png)
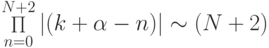 !
!При
![t \in \left[{t_N + 2\tau , t_N + 3\tau }\right]](/sites/default/files/tex_cache/07764372a4d152c9c214603512fa3762.png)
![$ \left|{R_N (t)}\right| \le \frac {(N + 2)(N + 3)}{2!} \tau ^{N + 1} \max\limits_{\xi \in [t_0, t_N + 3\tau ]} \left|{f^{(N + 1)}(\xi )}\right| $,](/sites/default/files/tex_cache/20ae65e442cf0c49838470515ed60f4f.png)
Видно, что ошибка экстраполяции растет быстро, но не сразу: экстраполяция
допустима на интервалах 
