Построение цикла с помощью инварианта

Нахождение корня функции методом деления отрезка пополам

Рассмотрим еще один пример использования схемы построения цикла с помощью инварианта, часто встречающийся в реальных программах. Пусть y = f(x) - непрерывная функция от вещественного аргумента, принимающая вещественные значения. Пусть известно, что на заданном отрезке [a,b] она принимает значения разных знаков. Из непрерывности функции f следует, что она имеет по крайней мере один корень на этом отрезке. Требуется вычислить корень функции f с заданной точностью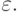

Идея алгоритма состоит в том, чтобы поделить отрезок пополам и выбрать ту половину отрезка, на которой функция принимает значения разных знаков. Эта операция повторяется до тех пор, пока длина отрезка не станет меньше, чем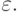

Пусть концы текущего отрезка хранятся в переменных x₀, x₁. Инвариантом цикла является утверждение о том, что функция принимает значения разных знаков в точках x₀, x₁:

I(x0, x1): f(x0)*f(x1) <= 0

Начальные значения:

x0 = a,  x1 = b

Условием завершения цикла является утверждение о том, что длина отрезка меньше

(знак модуля используется потому, что в условии задачи не требуется выполнения неравенства a < b ).

Выпишем алгоритм вычисления корня функции с заданной точностью:

вещ корень функции на отрезке(вх: вещ a, вещ b, вещ eps)
| дано: f(a) * f(b) <= 0,
|       eps > 0 - очень маленькое число;
| надо: вычислить корень функции f на отрезке [a, b] с
|       точностью eps;
начало алгоритма
| вещ x0, x1, c;
|
| // инициализация
| x0 := a; x1 := b;
| утверждение: f(x0) * f (x1) <= 0;
|
| цикл пока |x1 - x0| >= eps
| | инвариант: f(x0) * f (x1) <= 0;
| | c := (x0 + x1) / 2; // Середина отрезка [x0, x1]
| | если f(x0) * f(c) <= 0
| | | то
| | |   x1 := c
| | | иначе
| | |   утверждение: f(c) * f(x1) <= 0
| | |   x0 := c
| | конец если
| конец цикла
|
| утверждение: |x1 - x0| < eps  и
|              f(x0) * f (x1) <= 0;
| ответ := (x0 + x1) / 2;
конец алгоритма