Опубликован: 23.10.2009 | Уровень: для всех | Доступ: свободно
Лекция 2:
Понятие информации
Аннотация: В данной лекции содержатся сведения о единицах измерения информации, уточняются понятия: "информация как выбор" и "информация как смысл", дается определение искусственного интеллекта.
Ключевые слова: физическая модель, нечеткая логика, бинарное дерево, binary digit, пробельный символ, кодирование информации, экспонента, иррациональное число, счисление, информация, поток, бит, автор, тег, произвольное, значение, 1-грамматика, ПО, парадигма программирования, метаязык, алгоритмический язык, диаграмма Ганта, сетевой график, процедурный язык, дерево вывода, метод перебора, декларативный язык, цели проекта, мышление, электрическая схема, магистраль, логический вывод, двоичная система счисления, система счисления, обратная функция, чередование, рациональное число, транзистор, интегральная схема, позиционная система счисления, тождество, доказательство теорем, умозаключение, система команд, описание шрифта, кегль, verb, словосочетание, понимание текста, ассемблер, транслятор, материнская плата, слот, периферийное устройство
В этой части курса Вы познакомитесь:
- Что такое информация и чем ее измеряют;
- Что такое: "смысл" - с точки зрения информатики;
2.1. Информация как выбор
2.1.1. Степени свободы
Итак, информацию можно определить количеством возможных вариантов, в котором может находиться система, или которые может выбрать живое существо (или автомат) в процессе жизни (работы). Это количество вариантов называется в физике "степенями свободы". Для физики количество степеней свободы имеет первостепенное значение при расчете сложных систем и при моделировании химических и биохимических процессов. Зная все степени свободы системы, можно рассчитать все свойства системы (за исключением их изменения во времени).
2.1.2. Формализация выбора
Следующим необходимым этапом, который нужно пройти для понимания понятия информации, является определение вариантов выбора.
2.1.2.1. Логический выбор
Простейшим выбором является двухвариантный логический выбор. С его помощью осуществляется выбор между двумя значениями: "Да" и "Нет", "Истина" и "Ложь", "0" и "1", "Свет" и "Мрак" и т.д. Этот выбор легко моделировать на физических моделях: "рычаг влево" и "рычаг вправо", "включен" и "выключен", "есть ток" и "нет тока". Любая ЭВМ моделирует логический выбор с помощью физической модели. Это и является ее ограничением.
2.1.2.2. Многовариантный выбор
Логическим выбором не ограничиваются варианты выбора. Примером "альтернативного" выбора может служить выбор из трех вариантов: "Да", "Нет" и "Может быть". Есть в математике даже такой раздел: "Нечеткая логика", который рассматривает вероятность выбора в виде произвольного числа со значениями от "0" до "1". Именно "нечеткая логика" моделирует работу человеческого мозга, решающего любую задачу. На рисунке 2.1 нарисованы варианты логического (бинарного), тернарного и многозначного выбора.
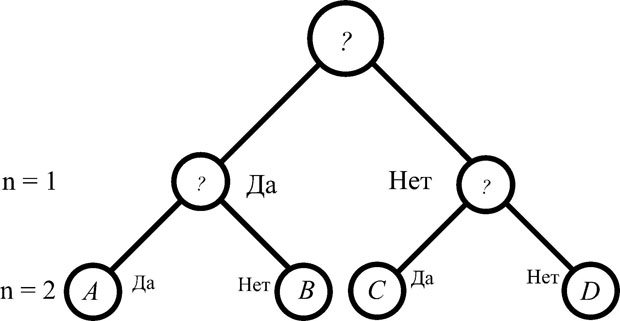
2.1.3. Моделирование многозначного выбора деревом бинарного выбора
Достоинством дерева бинарного вывода является возможность с помощью него моделировать практически любое количество выборов. Эта возможность проиллюстрирована на рисунках 2.2. и 2.3.
На рис. 2.2 рассматривается четырехвариантный выбор событий: "A", "B", "C" и "D". Он также может быть осуществим с помощью двух бинарных выборов по условиям:
- условие: "Это A или B?" ("Да" или "Нет");
- условие: "Это A?" ("Да" или "Нет");
- условие: "Это C?" ("Да" или "Нет").
Таким образом, используя только два вопроса, можно превратить тетрарный выбор в дерево бинарного вывода. На рис. 2.3 показан тернарный вывод, моделированный с помощью дерева бинарного вывода.
2.1.4. Мера информации
2.1.4.1. Практическая формула информации
Итак, мы выяснили, что выбор из почти любого количества вариантов можно моделировать с помощью бинарного дерева вывода. Для подсчета количества вариантов выбора может быть полезна формула:
 |
( 2.1) |
Используя вышеперечисленные рассуждения, в 1947 году американский математик Клод Шеннон применил следующее уравнение:
 |
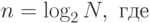( 2.2) |
-
- количество вариантов (степеней свободы), -
- количество информации.
Единицей количества информации стали называть бит (от английского: "BInary digiT", - двоичное число). Одному биту соответствует выбор из двух вариантов.
Теоретически число бит может быть дробным числом. Например, выбору из трех вариантов соответствует число: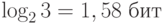 
. Каждая из 26 букв латинского алфавита содержит информацию 
.
На практике принято округлять количество бит в большую сторону к ближайшему целому. Так, информацию о трех вариантах выбора на практике округляется до двух бит, а информацию обо всех прописных и строчных буквах латинского алфавита вместе со знаками препинания, пробельными символами и цифрами приводят к значению 7 бит. Итак, формула практического вычисления количества информации:
 |
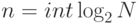( 2.3) |
Формула 2.3 очень полезна при кодировании информации с помощью компьютера. Вкратце скажем, что число бит по формуле 2.3 - это число ячеек в ЭВМ, занятых для представления информации из количеств вариантов.
2.1.4.2. Теоретическая формула
С точки зрения "правильной" теории за основание логарифма, с помощью которой "мера информации" будет минимальна при любом числе степеней свободы, необходимо принять число 
. Таким образом, теоретическое значение меры информации будет измеряться формулой 2.4.
 |
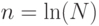( 2.4) |
где - мера информации, а - число выбора (степеней свободы) в системе.
Но использовать экспоненту в основании логарифма очень неудобно - ведь в этом случае мера информации ВСЕГДА будет представлена бесконечной дробью (т.н. иррациональным числом). На практике, как уже говорилось, удобно пользоваться основанием логарифма, равным двойке. Конечно, наилучшим приближением к экспоненте является число три. Более того, были созданы ЭВМ, которые использовали для представления чисел ячейки с тремя степенями свободы ("ток в прямом направлении", "тока нет", "ток в обратном направлении"). И эти ЭВМ на той же элементной базе считали намного быстрее! (Информация о таких ЭВМ была взята из журналов PC Week/RE и Computer World/RE за 2000-2004 г.). Но, из-за сложности реализации этих ЭВМ на элементной базе (то есть на кристалле полупроводника), такие системы так и остались экспериментальными ЭВМ.
В настоящее время стандартом стали системы обработки данных, использующие двоичную систему счисления.
2.1.5. Практическое исчисление меры информации
Автор понимает, что гуманитариям вовсе не нужно вычислять значения двоичного логарифма 
. Вместо этого автор предлагает использовать таблицу 2.1. Смысл этой таблицы следующий. В ней во втором столбце приводится количество вариантов , а в первом столбце - количество (в битах) этой информации. Если Вам, например, необходимо определить количество информации при выборе из 33 вариантов (все строчные русские буквы), то, посмотрев на столбец 2, мы можем видеть, что оно лежит между числами 32 и 64. Числу 64 в первом столбце соответствует число 6. Это значит, что все русские буквы можно закодировать минимум 6 битами.
| n | Представление степени n числа 2 | ||
|---|---|---|---|
| Десятичное | Восьмеричное | Шестнадцатеричное | |
| 0 | 1 | 1 | 1 |
| 1 | 2 | 2 | 2 |
| 2 | 4 | 4 | 4 |
| 3 | 8 | 10 | 8 |
| 4 | 16 | 20 | 10 |
| 5 | 32 | 40 | 20 |
| 6 | 64 | 100 | 40 |
| 7 | 128 | 200 | 80 |
| 8 | 256 | 400 | 100 |
| 9 | 512 | 1 000 | 200 |
| 10 | 1 024 | 2 000 | 400 |
| 11 | 2 048 | 4 000 | 800 |
| 12 | 4 096 | 10 000 | 1 000 |
| 13 | 8 192 | 20 000 | 2 000 |
| 14 | 16 384 | 40 000 | 4 000 |
| 15 | 32 768 | 100 000 | 8 000 |
| 16 | 65 536 | 200 000 | 10 000 |
| 17 | 131 072 | 400 000 | 20 000 |
| 18 | 262 144 | 1 000 000 | 40 000 |
| 19 | 524 288 | 2 000 000 | 80 000 |
| 20 | 1 048 576 | 4 000 000 | 100 000 |
| 21 | 2 097 152 | 10 000 000 | 200 000 |
| 22 | 4 194 304 | 20 000 000 | 400 000 |
| 23 | 8 388 608 | 40 000 000 | 800 000 |
| 24 | 16 777 216 | 100 000 000 | 1 000 000 |
| 25 | 33 554 432 | 200 000 000 | 2 000 000 |
| 26 | 67 108 864 | 400 000 000 | 4 000 000 |
| 27 | 134 217 728 | 1 000 000 000 | 8 000 000 |
| 28 | 268 435 456 | 2 000 000 000 | 10 000 000 |
| 29 | 536 870 912 | 4 000 000 000 | 20 000 000 |
| 30 | 1 073 741 824 | 10 000 000 000 | 40 000 000 |
| 31 | 2 147 483 648 | 20 000 000 000 | 80 000 000 |
| 32 | 4 294 967 296 | 40 000 000 000 | 100 000 000 |
Столбцы 3, 4 и 5 в таблице соответствуют двоичному, восьмеричному и шестнадцатеричному представлению чисел из столбца 2. Их смысл представлен в дальнейших лекциях. ("Кодирование").
2.2. Информация как смысл
С точки зрения гуманитария понятие информации ассоциируется только с понятием: "осмысленная информация". Смысл информации передают данные, которые как бы "зашиты" в поток бит, требуемых для их передачи. Однако в чем заключается "смысл"? Ответ на этот вопрос автор начал искать в энциклопедиях.
Изучение энциклопедий [104 БСЭ, 100 КРЭ, 102-103 ЭКМ] показало, что в науке смысл отождествляется со значением. Иначе говоря, смысл любого атрибута, тега, символа, переменной определяется его значением. Это, однако, не означает, что "забив" в тег произвольное значение, мы практически придадим тегу смысл. Это вовсе не так! На самом деле на значения атрибутов накладываются ограничения на принимаемые значения. Таким образом, осмысленная информация - это значение "тега", принимающее одно из его допустимых значений. Правила же, задающие определенные значения тегам, определяются описанием языка, прежде всего его грамматикой. При этом грамматика может иметь несколько уровней. На примере русского языка, это следующие уровни:
- Фонетика и графика;
- Орфография;
- Управление;
- Синтаксис предложений + пунктуация;
- Лексика и стиль изложения.
Более низкий уровень несет меньше "смысловой" информации, но содержит больше критических для понимания языка правил. Скажите, что Вас больше раздражает в иностранцах: их акцент или неумение искусно подбирать выражения на русском языке? Ответ очевиден - правильное произношение более критично для понимания, чем остальные недочеты речи. Более того, неправильное употребление лексики может служить определенным художественным приемом. Например, в детстве автор развлекал еще более младших ребят стихотворением:
Кровожадный серый заяц
Стал пугать слонов. На палец
Он одел сковороду,
Что была тогда в ходу.
Стал он в сковороду бить,
Стало всех слонов мутить.
При полном отсутствии смысла у этого стихотворения, оно имело большой успех у детей. По причине совпадения этого стиха с правилами русской грамматики и основами стихосложения, оно стало обладать комическим смыслом. То же относится к следующим предложениям.
На дворе стояла рота солдат и осень.
Шли двое мужчин и дождь. Один в сапогах, другой в кино, третий в летний вечер.
Это еще раз подтверждает: правила грамматики несут не меньше смысловой нагрузки, чем сам текст на этом языке.
