Изображение полиэдра
Решаемая задача изображения проекции полиэдра может быть разделена на две следующим образом: сначала вычислим плоское изображение проекции, состоящее из совокупности прямолинейных отрезков ребер (точнее, их видимых частей), а затем осуществим вывод этого изображения в специально созданном новом окне (более точное название для него — фрейм).
Задачу вывода плоского изображения в отдельном фрейме поручим осуществлять классу AwtDrawer. Графическая библиотека (пакет java.awt ) содержит среди множества других класс Frame, позволяющий создать фрейм и, используя простейшие графические примитивы, построить в нем требуемое изображение. Класс AwtDrawer будет являться расширением класса Frame, а основным методом рисования проекции отрезков ребер будет метод draw, изображающий прямолинейный отрезок. Координаты точек при этом предполагаются нормированными — и абсцисса и ордината должны быть заключены между нулем и единицей.
import java.awt.*;
public class AwtDrawer extends Frame {
private static final int XLEN = 500;
private static final int YLEN = 500;
private static final int DELTA= 100;
private Image offScrImage;
private Graphics offScrGC;
private Graphics g;
public AwtDrawer() {
super("Построение изображения полиэдра");
setSize(XLEN+2*DELTA, YLEN+2*DELTA);
setBackground(Color.white);
g = getGraphics();
show();
offScrImage = createImage(XLEN+2*DELTA, YLEN+2*DELTA);
offScrGC = offScrImage.getGraphics();
offScrGC.setColor(Color.white);
offScrGC.fillRect(0,0,XLEN+2*DELTA, YLEN+2*DELTA);
offScrGC.setColor(Color.black);
}
public final void draw(double xb, double yb, double xe, double ye) {
int x0 = DELTA + (int)(XLEN * xb);
int y0 = DELTA + (int)(YLEN * yb);
int x1 = DELTA + (int)(XLEN * xe);
int y1 = DELTA + (int)(YLEN * ye);
offScrGC.drawLine(x0, y0, x1, y1);
}
public void update(Graphics g) {
paint(g);
}
public void paint(Graphics g) {
g.drawImage(offScrImage, 0, 0, this);
}
}Поясним назначение некоторых констант, переменных и методов, которые встречаются в реализации класса AwtDrawer.
Первые три строки тела конструктора этого класса последовательно устанавливают заголовок создаваемого фрейма, его размер и цвет фона. Вокруг области рисования размером XLENxYLEN предусмотрены поля шириной DELTA.
Класс Graphics пакета AWT уже встречался нам при рассмотрении аплетов. Именно в нем определены все основные графические примитивы. По некоторым причинам, обсуждение которых выходит за рамки нашего курса, изображение сначала строится в так называемом внеэкранном буфере offScrImage, а во фрейм выводится с помощью метода drawImage при вызове методов paint и update. Метод draw, аргументами которого являются числа в диапазоне от 0 до 1, вычисляет соответствующие им координаты фрейма и с помощью метода drawLine рисует заданный отрезок.
Вернемся теперь к задаче определения множества отрезков на плоскости, которые должны быть изображены.
В качестве первого шага в этом направлении полезно решить относительно
простую
задачу построения проекции всех ребер полиэдра целиком. Создадим для этих
целей класс SimpleDrawer, который вполне логично сделать выведенным из
класса AwtDrawer. В качестве компонент в этот класс включим сам полиэдр,
ортонормированный базис, состоящий из нормированного вектора проектирования и
двух единичных ортогональных друг другу векторов в плоскости проекции,
минимальные значения  и
и  координат проекции вершин
полиэдра в
плоскости проекции и длину минимальной стороны квадрата, в который
целиком поместится вся проекция полиэдра.
координат проекции вершин
полиэдра в
плоскости проекции и длину минимальной стороны квадрата, в который
целиком поместится вся проекция полиэдра.
Ряд методов класса SimpleDrawer предназначен для нахождения координат
проекции произвольного трехмерного вектора, как реальных, так и нормализованных
(в той системе координат на плоскости проекции, в которой изображаемой части
фрейма соответствует квадрат 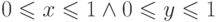 ). Вычисление реальных координат проекции, как это хорошо
известно
из аналитической геометрии, сводится к вычислению скалярных произведений с
помощью статического метода scalMul класса R3Vector, а
их нормализация — к линейному преобразованию (сдвигу и гомотетии).
). Вычисление реальных координат проекции, как это хорошо
известно
из аналитической геометрии, сводится к вычислению скалярных произведений с
помощью статического метода scalMul класса R3Vector, а
их нормализация — к линейному преобразованию (сдвигу и гомотетии).
public class SimpleDrawer extends AwtDrawer {
protected Polyedr p;
protected R3Vector pr;
private R3Vector x;
private R3Vector y;
private double xmin;
private double ymin;
private double size;
private double xProection(R3Vector v) {
return R3Vector.scalMul(v, x);
}
private double yProection(R3Vector v) {
return R3Vector.scalMul(v, y);
}
protected double xnProection(R3Vector v) {
return (xProection(v) - xmin)/size;
}
protected double ynProection(R3Vector v) {
return (yProection(v) - ymin)/size;
}
public SimpleDrawer(Polyedr p, R3Vector pr, double angle) {
this.p = p;
this.pr = pr.normalize();
double a = pr.getX();
double b = pr.getY();
double c = pr.getZ();
if (a != 0. || b != 0.) {
x = new R3Vector(-b, a, 0.);
} else {
x = new R3Vector(0., c, -b);
}
y = R3Vector.vectMul(x, pr);
x.normalize();
y.normalize();
R3Vector nx = R3Vector.plus(R3Vector.mul(Math.cos(angle), x),
R3Vector.mul(-Math.sin(angle), y));
R3Vector ny = R3Vector.plus(R3Vector.mul(Math.sin(angle), x),
R3Vector.mul(Math.cos(angle), y));
x = nx;
y = ny;
xmin = ymin = Double.MAX_VALUE;
double xmax, ymax;
xmax = ymax = Double.MIN_VALUE;
for (int i=0; i<p.getVertexesQuantity(); i++) {
double xi = xProection(p.getVertex(i));
double yi = yProection(p.getVertex(i));
if (xi < xmin) xmin = xi;
if (yi < ymin) ymin = yi;
if (xi > xmax) xmax = xi;
if (yi > ymax) ymax = yi;
}
size = ymax - ymin;
if (xmax - xmin > size) size = xmax - xmin;
}
public final void draw() {
for (int i=0; i<p.getEdgesQuantity(); i++)
drawEdge(p.getEdge(i));
Xterm.print("\n");
}
public void drawEdge(Edge s) {
Vertex begin = s.getBegin();
Vertex end = s.getEnd();
draw(xnProection(begin), ynProection(begin),
xnProection(end), ynProection(end));
Xterm.print(".");
}
}Всю основную подготовительную работу выполняет конструктор класса. Первой из
его задач является нахождение ортонормированного базиса, одним из векторов
которого является вектор проектирования единичной длины. Нормализация
вектора осуществляется при этом с помощью метода normalize класса R3Vector. Второй из векторов искомой тройки строится с помощью уже
найденного вектора нормали (нормированному вектору проектирования) по
следующему правилу.
Если 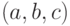 — координаты вектора нормали, то векторы с
координатами
— координаты вектора нормали, то векторы с
координатами 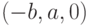 и
и 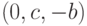 оба ему ортогональны, и при этом
один из них заведомо
не нулевой. Он-то и
выбирается в качестве второго из векторов базиса (в программной реализации ему
соответствует компонента x класса SimpleDrawer ).
оба ему ортогональны, и при этом
один из них заведомо
не нулевой. Он-то и
выбирается в качестве второго из векторов базиса (в программной реализации ему
соответствует компонента x класса SimpleDrawer ).
Третий вектор базиса (компонента y ) находится с помощью вычисления
векторного произведения
(метод vectMul ) двух уже найденных. Заключительным шагом является
осуществление поворота на заданный угол angle в плоскости проекции.
Как известно из аналитической геометрии, поворот в плоскости  на угол
на угол  эквивалентен умножению вектора координат
эквивалентен умножению вектора координат  на матрицу
на матрицу
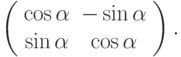
Вторая задача конструктора класса SimpleDrawer — определение квадрата наименьшего размера, в котором целиком поместится проекция всех ребер полиэдра. Способ индуктивного вычисления минимального и максимального значений последовательности координат вершин нам хорошо известен. Определение длины стороны искомого квадрата после этого сводится к выбору максимальной из двух длин сторон найденного ограничивающего прямоугольника проекции.
Метод draw, который и должен построить проекцию полиэдра, осуществляет это с помощью метода drawEdge, последовательно вызываемого для всех ребер. Последний из методов вычисляет нормализованные координаты проекции обрабатываемого ребра и вызывает метод draw базового класса AwtDrawer для рисования требуемого отрезка. Так как для сложных полиэдров их изображения могут строиться достаточно долго, а визуализация результата происходит только после полного завершения решения задачи, то рисование каждого ребра во внеэкранном буфере заканчивается выводом точки на экран терминала. Появляющаяся при этом последовательность точек позволяет следить за процессом построения изображения.
Наиболее содержательная часть исходной задачи — учет затенения частей ребер гранями полиэдра — будет решаться с помощью класса ShadowDrawer, обсуждению которого посвящена следующая секция параграфа. В ней выяснится, что для работы с тенями (точнее с просветами — дополнениями теней) целесообразно создать еще два класса — Segment и L1ListSegments.
Чуть позже будет рассмотрен и один из возможных методов оптимизации, позволяющий ускорить построение изображения сложных полиэдров, содержащих десятки тысяч ребер и тысячи граней, с помощью так называемого двумерного хеширования граней. Для этих целей будет создан специальный класс SmartDrawer.
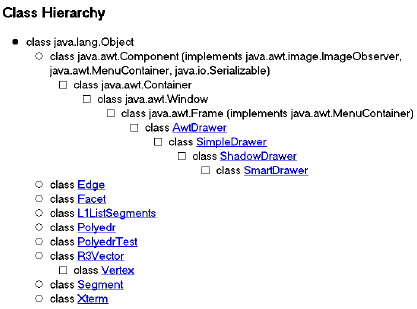
Метод main, выполняющий ввод имени файла с описанием изображаемого полиэдра, конкретного способа изображения, вектора проектирования и угла поворота в плоскости проекции, реализуется в отдельном классе PolyedrTest, которым завершается построение иерархии классов, используемых для решения исходной задачи. Все классы иерархии показаны на рисунке рис. 13.3.