Высказывания и предикаты
Синтаксис языка предикатов
Так как нам предикаты нужны прежде всего для описания программ, введем следующее определение.
Определение 3.1. Высказывание или предикат — это
функция, действующая из
некоторого множества значений переменных программы (идентификаторов) в
множество из двух значений {  ,
,  } ( Да и Нет ).
} ( Да и Нет ).
В соответствии с ним предикатами будут следующие фразы:
- значение переменной i равно двум;
- переменная k положительна, а значение переменной m при этом не превосходит 100;
- значения всех целочисленных переменных программы являются нулевыми;
- неправда, что значение переменной i неположительно.
Чуть менее понятно, можно ли считать предикатами такие фразы:
- если предположить, что значение переменной i равно двум, то значения всех остальных целочисленных переменных программы будут неотрицательными;
- данная программа является правильной;
- данное высказывание ложно.
Особенно показательным является последний пример. Если мы согласимся с тем, что он представляет из себя предикат, то возникает естественный вопрос о его истинности. Предположение о том, что он истинен, заставляет считать его ложным, и наоборот. Получаемое противоречие говорит о том, что определение 3.1 не является достаточно корректным.
Ситуация с предикатами напоминает уже обсуждавшуюся нами ситуацию с языками для записи алгоритмов — необходим какой-то четкий критерий, позволяющий однозначно определить, что является предикатом, а что нет.
В теории формальных языков, более детальное знакомство с которой состоится позже, принято задавать язык с помощью грамматики. Грамматику же достаточно часто определяют с помощью так называемой нормальной формы Бэкуса-Наура (НФБН). Вот все необходимые общие определения.
Определение 3.2. Алфавит  — произвольное непустое множество.
— произвольное непустое множество.
Мы будем иметь дело только с конечными алфавитами, примерами которых являются алфавит русского языка, английский алфавит, множество цифр, алфавит всех символов, имеющихся на клавиатуре компьютера.
Определение 3.3. Символом алфавита  называют любой его элемент, а цепочкой над алфавитом — произвольную последовательность символов
называют любой его элемент, а цепочкой над алфавитом — произвольную последовательность символов  .
.
Цепочки часто называют также словами, фразами и предложениями. Пустая
цепочка
обозначается специальным символом  , а множество всех
цепочек над
алфавитом
, а множество всех
цепочек над
алфавитом  принято обозначать
принято обозначать  .
Если в качестве
.
Если в качестве  взять множество букв русского алфавита,
дополненное
символом пробела и знаками пунктуации, то в
взять множество букв русского алфавита,
дополненное
символом пробела и знаками пунктуации, то в  будут
содержаться
все фразы русского языка.
будут
содержаться
все фразы русского языка.
Определение 3.4. Длиной 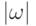 цепочки
цепочки 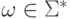 называется количество входящих в нее символов.
называется количество входящих в нее символов.
Длина пустой цепочки равна нулю, а длины всех остальных цепочек над любым алфавитом положительны.
Определение 3.5.
Операция 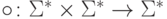 конкатенации двух цепочек определена следующем образом.
Пусть
конкатенации двух цепочек определена следующем образом.
Пусть  ,
, 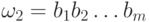 ,
тогда
,
тогда 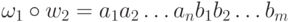 .
.
Операция конкатенации, называемая также операцией сцепления или дописывания, обладает следующими свойствами.
Предложение 3.1.
Для любых цепочек  ,
, 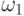 ,
, 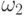 и
и 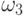 справедливы
следующие равенства:
справедливы
следующие равенства:
1) 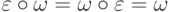 ,
,
2)  .
.
Имея все эти определения, уже можно дать формальное определения языка
над алфавитом  .
.
Определение 3.6. Язык  — это произвольное подмножество множества
цепочек
— это произвольное подмножество множества
цепочек  .
.
Если язык конечен, то есть состоит из конечного множества входящих в него цепочек, то его можно задать, просто перечислив все его элементы. Для бесконечных языков, которые чаще всего и представляют наибольший интерес, такой способ не годится. Достаточно часто для задания языка используют грамматику, несколько упрощенное определение которой мы сейчас рассмотрим.
Определение 3.7.
Пусть  — некоторый алфавит,
— некоторый алфавит,  —
метаалфавит, т.е. какой-то
другой алфавит, не пересекающийся с
—
метаалфавит, т.е. какой-то
другой алфавит, не пересекающийся с  (
( 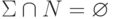 ).
Элементы метаалфавита
).
Элементы метаалфавита  называются метасимволами. Грамматикой
называются метасимволами. Грамматикой  называется набор (
называется набор (  ), где
), где  — множество символов,
— множество символов,  — множество метасимволов,
— множество метасимволов,  — множество правил
вывода вида:
— множество правил
вывода вида:  , где
, где  — какой-то
метасимвол,
— какой-то
метасимвол, 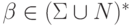 — произвольная цепочка над
объединением двух
алфавитов, и для каждого
— произвольная цепочка над
объединением двух
алфавитов, и для каждого  встречается хотя бы одно
правило с
встречается хотя бы одно
правило с  в левой части (до стрелочки), а
в левой части (до стрелочки), а 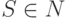 —
так называемый стартовый метасимвол.
—
так называемый стартовый метасимвол.
Содержательно каждое правило грамматики имеет смысл подстановки. Например,
строка 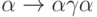 означает возможность
замены
метасимвола
означает возможность
замены
метасимвола  на цепочку
на цепочку  .
Начав со стартового
символа и пользуясь различными правилами грамматики, мы можем получать
различные цепочки из символов, которые называются выводимыми
цепочками.
.
Начав со стартового
символа и пользуясь различными правилами грамматики, мы можем получать
различные цепочки из символов, которые называются выводимыми
цепочками.
Заметим, что если в цепочке встречается метасимвол, то ее можно
преобразовать
дальше, применив одно из правил грамматики с этим метасимволом в левой части.
Если же метасимволов в цепочке не осталось, то процесс ее преобразования
закончен и больше с цепочкой ничего сделать нельзя. По этой причине обычные
символы (из алфавита  ) часто называют терминалами,
а метасимволы (из
) часто называют терминалами,
а метасимволы (из  ) — нетерминалами.
) — нетерминалами.
Определение 3.8. Языком 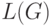 , порожденным грамматикой
, порожденным грамматикой  ,
называется множество всех
терминальных выводимых цепочек.
,
называется множество всех
терминальных выводимых цепочек.
Для задания грамматики часто используют очень наглядную форму представления,
называемую нормальной формой Бэкуса-Наура (НФБН).
Набор правил  задают при этом в виде совокупности правил со
стрелочками,
перечисляющими все возможные цепочки, на которые может быть заменен
каждый из метасимволов грамматики в процессе вывода, а стартовым метасимволом
считается тот, который присутствует в левой части самого первого правила.
задают при этом в виде совокупности правил со
стрелочками,
перечисляющими все возможные цепочки, на которые может быть заменен
каждый из метасимволов грамматики в процессе вывода, а стартовым метасимволом
считается тот, который присутствует в левой части самого первого правила.
В качестве примера дадим строгое определение языка предикатов, или, как принято еще говорить, зададим синтаксис этого языка.
Определение 3.9. Множество предикатов — это язык, порожденный следующей грамматикой:
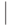
 (6-е правило: условное Или )
(6-е правило: условное Или )
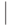
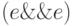 (8-е правило: условное И )
(8-е правило: условное И )
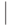
 (10-е правило: эквивалентность)
(10-е правило: эквивалентность)
Единственным метасимволом данной грамматики является  , а
алфавит
, а
алфавит 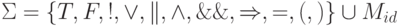 , где множество
, где множество 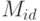 состоит из всех
возможных идентификаторов
(имен) переменных программ логического типа.
состоит из всех
возможных идентификаторов
(имен) переменных программ логического типа.
Приведем пример цепочки вывода в данной грамматике: 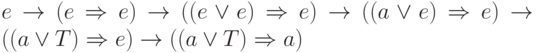 . Этo показывает, что выражение
. Этo показывает, что выражение 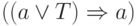 является предикатом. Легко построить
другой
вывод этого же предиката:
является предикатом. Легко построить
другой
вывод этого же предиката: 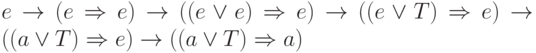 .
Существует и еще несколько других цепочек вывода для предиката
.
Существует и еще несколько других цепочек вывода для предиката 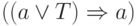 , отличающихся порядком замены
метасимвола
, отличающихся порядком замены
метасимвола  на
идентификатор
на
идентификатор  и значение
и значение  . Ясно, что в
определенном смысле,
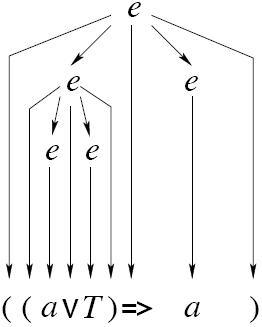
который мы не будем сейчас уточнять, все эти цепочки эквивалентны. Говорят,
что множество эквивалентных цепочек задает дерево вывода данного
предиката, изображенное на рисунке 3.1.
. Ясно, что в
определенном смысле,
который мы не будем сейчас уточнять, все эти цепочки эквивалентны. Говорят,
что множество эквивалентных цепочек задает дерево вывода данного
предиката, изображенное на рисунке 3.1.
Рассмотрим следующую задачу.
Задача 3.2. Докажите, что выражение  является предикатом.
является предикатом.
Решение Для доказательства достаточно предъявить вывод в грамматике 3.9
предложенного выражения, что не слишком трудно: 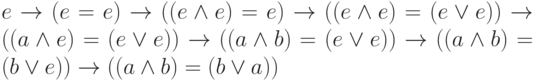 .
.
Покажем, как можно доказать, что выражение не является предикатом.
Задача 3.3. Докажите, что выражение  — не предикат.
— не предикат.
Решение В самом деле, для того, чтобы в предикате появился символ 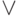 ,
необходимо
применить правило
,
необходимо
применить правило 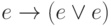 , а его применение
вызывает
появление пары скобок, которых нет в выражении
, а его применение
вызывает
появление пары скобок, которых нет в выражении 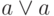 . Ни один
из
терминальных символов, появившись в процессе вывода, не может измениться в
дальнейшем (или исчезнуть). Таким образом, если 5-е правило
грамматики 3.9 не применять, то
мы не сумеем
получить в итоговой цепочке символ
. Ни один
из
терминальных символов, появившись в процессе вывода, не может измениться в
дальнейшем (или исчезнуть). Таким образом, если 5-е правило
грамматики 3.9 не применять, то
мы не сумеем
получить в итоговой цепочке символ 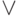 , а если его применить
хотя бы раз,
то в цепочке будут присутствовать скобки. Полученное противоречие и показывает,
что выражение
, а если его применить
хотя бы раз,
то в цепочке будут присутствовать скобки. Полученное противоречие и показывает,
что выражение  предикатом не является.
предикатом не является.


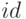 (3-е правило:
(3-е правило:  (4-е правило:
(4-е правило: 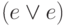 (5-е правило:
(5-е правило: 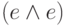 (7-е правило:
(7-е правило:  (9-е правило:
(9-е правило: