Все задачи курса
Все задачи лекций 8-10
Полным решением задач, приведенных ниже, не может считаться только текст правильно написанной программы. Во всех случаях необходимо изложение теоретической части решения и описание соответствия между переменными программы и обозначениями, использованными при теоретическом исследовании.
Задачи на рекурсию
При решении задач из этого раздела необходимо обосновать как то, почему программа заканчивает работу, так и то, почему после ее завершения будет получен требуемый результат.
Задача 11.1. Напишите рекурсивную программу, перемножающую два целых числа, одно из
которых неотрицательно, без использования операции умножения. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить 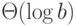 , таковы:
, таковы:  ,
, 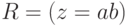 . Числа
. Числа  и
и  в программе изменять нельзя.
в программе изменять нельзя.
Задача 11.2. Напишите программу, печатающую значение многочлена степени  в заданной точке
в заданной точке  . Коэффициенты многочлена хранятся в
массиве
. Коэффициенты многочлена хранятся в
массиве  в порядке убывания степеней и являются целыми числами, также
как и значение
в порядке убывания степеней и являются целыми числами, также
как и значение  . Величины
. Величины  ,
,  и элементы массива
и элементы массива  изменять в
программе нельзя.
изменять в
программе нельзя.
Задача 11.3. Напишите рекурсивную программу, печатающую значение производной
многочлена степени  в
заданной точке
в
заданной точке  . Коэффициенты многочлена хранятся в массиве
. Коэффициенты многочлена хранятся в массиве  в порядке убывания степеней и являются целыми числами, так же как и
значение
в порядке убывания степеней и являются целыми числами, так же как и
значение  . Величины
. Величины  ,
,  и элементы массива
и элементы массива  изменять в
программе нельзя.
изменять в
программе нельзя.
Указание
Пусть  .
Продифференцируем по
.
Продифференцируем по  равенство
равенство  и подставим затем
и подставим затем  . Мы получим
следующие соотношения:
. Мы получим
следующие соотношения:
 ,
,
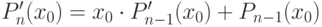 .
.
Воспользовавшись ими и формулами
 ,
,
 ,
,
легко определить рекурсивную функцию неотрицательного целого аргумента  ,
, 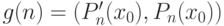 для вычисления которой и пишется программа.
для вычисления которой и пишется программа.
Проектирование цикла при помощи инвариантa
При решении задач из этого раздела необходимо построить и доказать правильность построенной программы вида "S0;while(e)S;", а при отсутствии в условии задачи явно заданных инварианта цикла и ограничивающей функции объяснить предварительно, каким образом они были получены.
Задача 11.4. Напишите программу, перемножающую два целых числа, одно из
которых неотрицательно, без использования операции умножения. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить 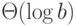 , таковы:
, таковы:  ,
, 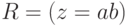 . При написании программы величины
. При написании программы величины  и
и  изменять не
разрешается, следует использовать инвариант
изменять не
разрешается, следует использовать инвариант 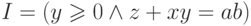 и ограничивающую функция
и ограничивающую функция  .
.
Задача 11.5. Напишите программу, возводящую целое число в целую
неотрицательную степень. Точные
пред- и постусловия требуемой программы таковы:  ,
, 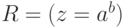 .
При написании программы величины
.
При написании программы величины  и
и  изменять не
разрешается, следует использовать инвариант
изменять не
разрешается, следует использовать инвариант  и ограничивающую функцию
и ограничивающую функцию  .
.
Задача 11.6. Напишите программу, находящую приближенное значение квадратного корня  из заданного неотрицательного целого числа
из заданного неотрицательного целого числа  . Вот более
точная формулировка пред- и постусловия:
. Вот более
точная формулировка пред- и постусловия:  ,
,  . При написании программы величину
. При написании программы величину  изменять нельзя.
изменять нельзя.
Задача 11.7. Напишите программу (линейный поиск), определяющую первое вхождение
заданного целого числа  в заданный массив
в заданный массив ![b[0..m-1]](/sites/default/files/tex_cache/4076bda9f74e4a0083e3d3e407de4f68.png) целых чисел (
целых чисел (  ).
Известно, что
).
Известно, что  находится в массиве
находится в массиве  .
Значения элементов массива
.
Значения элементов массива  и число
и число  в программе изменять нельзя.
в программе изменять нельзя.
Задача 11.8. Напишите программу, находящую сумму  элементов заданного целочисленного
массива
элементов заданного целочисленного
массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) , элементы которого и величину
, элементы которого и величину  изменять нельзя.
Точные пред-
и постусловия:
изменять нельзя.
Точные пред-
и постусловия:  ,
,
![\displaystyle R=\left(s = \sum_{j=0}^{n-1} b[j]\right).](/sites/default/files/tex_cache/925b14b983a8f78ecce564b23e49c49b.png)
Задача 11.9. Напишите программу, находящую приближенное значение квадратного корня  из заданного неотрицательного целого числа
из заданного неотрицательного целого числа  . Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить
. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить  , таковы:
, таковы:  ,
,  . При написании программы величину
. При написании программы величину  изменять нельзя.
изменять нельзя.
Задача 11.10. Найдите минимальное число, содержащееся в каждом из трех упорядоченных по возрастанию массивов целых чисел, в предположении, что таковое существует.
Задача 11.11. Напишите программу, печатающую  -ое число Фибоначчи
(
-ое число Фибоначчи
( 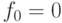 ,
, 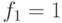 ,
,  ).
При написании программы используйте
).
При написании программы используйте  ,
,  ,
, 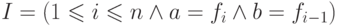 ,
, 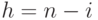 . Число
. Число  в программе изменять нельзя.
в программе изменять нельзя.
Задача 11.12. Напишите программу, находящую частное  и остаток
и остаток  от
деления
от
деления  на
на  , не использующую операций умножения и деления.
При написании программы положите
, не использующую операций умножения и деления.
При написании программы положите  ,
, 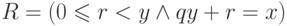 ,
, 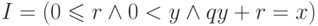 ,
,  . Величины
. Величины  и
и  в программе изменять не разрешается.
в программе изменять не разрешается.
Задача 11.13. Напишите программу, находящую наибольший общий делитель 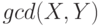 двух целых положительных чисел
двух целых положительных чисел  и
и  , не использующую операций
умножения и деления и не изменяющую величин
, не использующую операций
умножения и деления и не изменяющую величин  и
и  . При написании
программы положите
. При написании
программы положите  ,
, 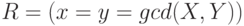 ,
,  ,
, 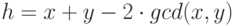 .
.
Указание Воспользуйтесь следующими свойствами наибольшего общего делителя двух чисел не равных одновременно нулю (не забудьте научиться доказывать все эти свойства):
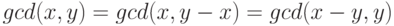 ,
,
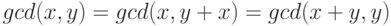 ,
,
 ,
,  ,
, 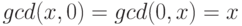 .
.
Задача 11.14. Напишите программу, находящую приближенное значение квадратного корня  из заданного неотрицательного целого числа
из заданного неотрицательного целого числа  . Вот более
точная формулировка пред- и постусловия:
. Вот более
точная формулировка пред- и постусловия: 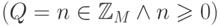 ,
,  . При написании программы величину
. При написании программы величину  изменять нельзя.
Для построения инварианта удалите из постусловия конъюнктивный член
изменять нельзя.
Для построения инварианта удалите из постусловия конъюнктивный член  . Оцените временную сложность получившейся программы
и сравните ее со сложностью программы, построенной в
задаче 9.1.
. Оцените временную сложность получившейся программы
и сравните ее со сложностью программы, построенной в
задаче 9.1.
Задача 11.15. Напишите программу, определяющую первое вхождение
заданного целого числа  в заданный массив массивов
в заданный массив массивов ![b[0..m-1][0..n-1]](/sites/default/files/tex_cache/992f5784919673248755220987a84823.png) целых чисел (
целых чисел (  ). Значения элементов массива
). Значения элементов массива  и числа
и числа  ,
,  и
и  в программе
изменять нельзя.
В момент завершения должно быть либо
в программе
изменять нельзя.
В момент завершения должно быть либо ![b[i][j] = x](/sites/default/files/tex_cache/5693da86fdd2dd8ac4968cc6630a5076.png) , либо, если числа
, либо, если числа  в массиве нет,
в массиве нет, 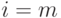 . Точные
пред- и постусловия требуемой программы таковы:
. Точные
пред- и постусловия требуемой программы таковы: 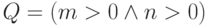 ,
, ![R=((0\leqslant i <m \land 0 \leqslant j < n \land x = b[i][j])\lor
(i=m \land x \notin b[0..m-1][0..n-1]))](/sites/default/files/tex_cache/83d6ee27e1bafd0c1840c7dba4718a06.png) .
.
Указание
Используйте инвариант, утверждающий, что  не находится в уже проверенных строках
не находится в уже проверенных строках ![b[0..i-1]](/sites/default/files/tex_cache/89a28517a4f9b174038303b26dbd6322.png) и среди уже
проверенных элементов
и среди уже
проверенных элементов ![b[i][0..j-1]](/sites/default/files/tex_cache/4fbbcce2466bf9552a940b09b5e1c8ea.png) текущей строки
текущей строки  .
В качестве ограничивающей функции возьмите
.
В качестве ограничивающей функции возьмите  .
.
Задача 11.16. Напишите программу (бинарный или двоичный поиск), определяющую
для упорядоченного по неубыванию массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) целых чисел
и заданного целого числа
целых чисел
и заданного целого числа  позицию
позицию  , в которую может быть вставлено
это число без нарушения упорядоченности массива. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить
, в которую может быть вставлено
это число без нарушения упорядоченности массива. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить  , таковы:
, таковы: ![Q=(x\in \mathbb{Z}_M \land n\in \mathbb{Z}_M \land n >0
\land (\forall j\ 0 \leqslant j < n-1\colon b[j] \leqslant b[j+1]))](/sites/default/files/tex_cache/94892ee8f93d8fac4926b38f9c816139.png) ,
, ![R=(
(i=-1\land x < b[0])\lor
(0\leqslant i < n-1\land b[i] \leqslant x < b[i+1])\lor
(i=n\land b[n-1] \leqslant x)
)](/sites/default/files/tex_cache/a6206a0a001b9bf1402f0ea1ca13a77b.png) . При написании программы величины
. При написании программы величины  ,
,  и элементы массива
и элементы массива  изменять
не разрешается, для построения инварианта используйте метод замены
константы переменной.
изменять
не разрешается, для построения инварианта используйте метод замены
константы переменной.
Задача 11.17. Напишите программу, печатающую факториал введенного неотрицательного целого числа, изменять которое нельзя. Для построения инварианта используйте метод замены константы переменной.
Задача 11.18. Напишите программу, находящую наибольшее целое число, являющееся
степенью двойки, не превосходящее заданного натурального числа  , изменять которое в программе нельзя.
, изменять которое в программе нельзя.
Указание Сначала выпишите формальную спецификацию программы, а затем постройте инвариант с помощью метода устранения конъюнктивного члена.
Задача 11.19. Напишите программу, находящую сумму  элементов заданного целочисленного
массива
элементов заданного целочисленного
массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) , элементы которого и величину
, элементы которого и величину  изменять нельзя.
Точные пред-
и постусловия:
изменять нельзя.
Точные пред-
и постусловия:  ,
,
![\displaystyle R=\left(s = \sum_{j=0}^{n-1} b[j]\right).](/sites/default/files/tex_cache/925b14b983a8f78ecce564b23e49c49b.png)
 в постусловии
в постусловии  новой переменной
новой переменной  .
.Задача 11.20. Напишите программу, находящую приближенное значение квадратного корня  из заданного неотрицательного целого числа
из заданного неотрицательного целого числа  . Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить
. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить  , таковы:
, таковы:  ,
,  . При написании программы величину
. При написании программы величину  изменять нельзя,
а инвариант следует построить методом замены константы
изменять нельзя,
а инвариант следует построить методом замены константы  на переменную
на переменную  в конъюнктивном члене
в конъюнктивном члене  постусловия
постусловия  .
.
Задача 11.21. Напишите программу, находящую наименьшее значение  в заданном массиве целых чисел
в заданном массиве целых чисел ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) , где
, где  .
Значения элементов массива
.
Значения элементов массива  и число
и число  в программе изменять нельзя,
в программе изменять нельзя,  ,
, ![R=(
(\forall j\ 0\leqslant j <n\ x \leqslant b[j])\land
(\exists k\ 0\leqslant k <n\ x = b[k]))](/sites/default/files/tex_cache/41b03e705805bb358b28ee74811f2a81.png) , инвариант постройте методом замены
константы
, инвариант постройте методом замены
константы  на переменную
на переменную  .
.
Задача 11.22. Напишите программу, находящую длину 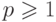 самой длинной
площадки в упорядоченном
по неубыванию массиве
самой длинной
площадки в упорядоченном
по неубыванию массиве ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) целых чисел. Площадкой мы называем
последовательность нескольких равных значений.
Значения элементов массива
целых чисел. Площадкой мы называем
последовательность нескольких равных значений.
Значения элементов массива  и число
и число  в программе изменять нельзя,
в программе изменять нельзя, ![Q=(n\in \mathbb{Z}_M \land n>0\land
(\forall j\ 0 \leqslant j < n-1\ b[j] \leqslant b[j+1]))](/sites/default/files/tex_cache/47d7b57881b5ace50cb8e45ba6c8e131.png) ,
, ![R=(
((\exists k\ 0\leqslant k \leqslant n-p\ b[k]=b[k+p-1])\land
(\forall j\ 0\leqslant j \leqslant n-p+1\ b[j] \ne b[j+p])))](/sites/default/files/tex_cache/6cd32ed6e7ad36a3a2f404818eec56da.png) ,
инвариант постройте методом замены константы
,
инвариант постройте методом замены константы  на переменную
на переменную  .
.
Задача 11.23. Напишите программу, находящую число  площадок в упорядоченном
по неубыванию массиве
площадок в упорядоченном
по неубыванию массиве ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) целых чисел. Площадкой мы называем
последовательность нескольких равных значений.
Значения элементов массива
целых чисел. Площадкой мы называем
последовательность нескольких равных значений.
Значения элементов массива  и число
и число  в программе изменять нельзя.
в программе изменять нельзя.
Указание Воспользуйтесь формулировкой предыдущей задачи.
Задача 11.24. Напишите программу, печатающую значение многочлена степени  в
заданной точке
в
заданной точке  . Коэффициенты многочлена хранятся в массиве
. Коэффициенты многочлена хранятся в массиве  в порядке убывания степеней и являются целыми числами, так же как и
значение
в порядке убывания степеней и являются целыми числами, так же как и
значение  . Величины
. Величины  ,
,  и элементы массива
и элементы массива  изменять в
программе нельзя.
Для построения инварианта используйте метод замены
константы переменной.
изменять в
программе нельзя.
Для построения инварианта используйте метод замены
константы переменной.
