|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Цифровая подпись
Стандарт цифровой подписи (DSS)
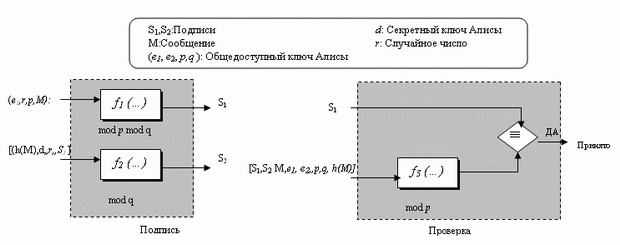
Стандарт цифровой подписи (DSS - Digital Signature Standard) был принят национальным Институтом Стандартов и Технологии (NIST) в 1994 г. NIST издал DSS как FIPS-186 (FEDERAL INFORMATION PROCESSING STANDARD 186). DSS применяет алгоритм цифровой подписи (DSA), основанный на схеме Эль-Гамаля, с использованием некоторых идей из схемы Шнорра. DSS критиковался со времени его издания. Главная претензия - оценка безопасности проекта DSS. Вторая - размер простого числа, 512 битов. Позже NIST сделал это число переменного размера, чтобы ответить на эту претензию. рис. 3.13 дает общую идею схемы DSS.
В процессе подписания две функции создают две подписи; в процессе проверки выход одной функции сравнивается с первой подписью для проверки. Это подобно схеме Шнорра, но входы различны. Другое отличие: эта схема использует дайджест сообщения (не само сообщение) как часть входов к функциям 1 и 3. Интересно то, что схема применяет два общедоступных модуля: p и q. Функции 1 и 3 используют оба модуля p и q, функция 2 - только q. Детали входов и функций коротко рассматриваются ниже.
Генерация ключей
Перед подписанием сообщения к любому объекту Алиса должна генерировать ключи и объявить общедоступные ключи.
- Алиса выбирает простое число длиной p. между 512 и 1024 битами. Число битов в p должно быть кратно числу 64.
- Алиса выбирает простое число на 160 битов q с таким условием, чтобы оно делилось на (p - 1).
- Алиса использует две группы умножения, <Zp*, x > и <Zq* ,x > ; вторая - подгруппа первой.
- Алиса создает e1, такое, чтобы оно было q -тым корнем 1 по модулю p (e1p = 1 mod p). Она поступает так: выбирает элемент в Zp, e0, и вычисляет e1 = e0(p-1)/q mod p.
- Алиса выбирает d как секретный ключ и вычисляет e2 = e1d
- Общедоступный ключ Алисы - (e1, e2, p, q), ее секретный ключ - (d).
Подписание и проверка
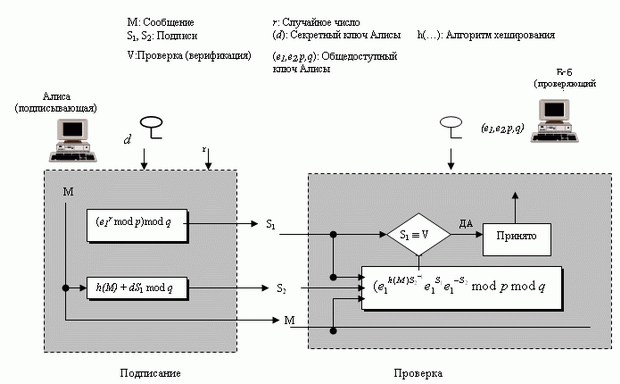
Рисунок 3.14 показывает схему DSS.
Подписание. Ниже показаны шаги подписания сообщения.
- Алиса выбирает случайное число (1 <= r <= q). Обратите внимание, что хотя открытые и секретные ключи могут быть выбраны один раз и использоваться для того, чтобы подписать много сообщений, Алиса должна выбирать каждый раз новый r, когда она должна подписать новое сообщение.
- Алиса вычисляет первую подпись S1 = (e1 mod p) mod q. Обратите внимание: значение первой подписи не зависит от М (сообщения).
- Алиса создает дайджест сообщения h (M).
- Алиса вычисляет вторую подпись S2 = (h(M) + dS1)r-1mod q. Обратите внимание, что вычисление S2 делается по модулю q.
- Алиса посылает M, S1 и S2 Бобу.
Проверка (верификация). Для проверки сообщения обычно применяются следующие шаги, когда получены М, S1 и S2.
- Боб проверяет S1 0 < S1 < q.
- Боб проверяет S2 0 < S2 < q.
- Боб вычисляет дайджест М, применяя алгоритм хэширования, используемый Алисой.
- Боб вычисляет V = [(e1h(M)/S2 e2S1/S2) mod p] mod q.
- Если S конгруэнтен V, сообщение принимается; иначе - отклоняется.
Пример 3.5
Алиса выбирает q = 101 и p = 8081. Алиса выбирает e0 = 3 и вычисляет e1 = e0(p-1)/q mod p = 6968. Алиса выбирает d = 61 в качестве секретного ключа и вычисляет e2 = e1d mod p = 2038. Теперь Алиса может передать сообщение Бобу. Предположим, что h (M) = 5000, и Алиса выбирает r = 61:
h(M) = 5000 r =61 S1 = (e1r mod p) mod q = 54 S2 = (h(M) + dS1)r-1 mod q = 40 S2-1 = 48 mod 101 V = [(69685000 x 48 x 203854 x 48 x 203854 x 48)mod 8081]mod 101 = 54
Поскольку Sj и V являются подходящими, Боб принимает сообщение.
Сравнение DSS и RSА
Вычисление DSS-подписи быстрее, чем вычисление подписей RSА, при использовании того же самого p.
Сравнение DSS и схемы Эль-Гамаля
DSS-подпись - меньше, чем подписи в схеме Эль-Гамаля, потому что q меньше, чем p.
Схема цифровой подписи эллиптической кривой
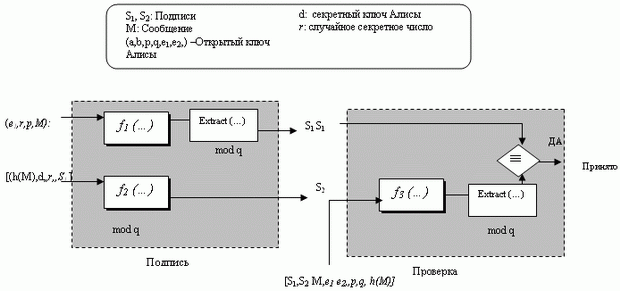
Наша последняя схема - схема цифровой подписи эллиптической кривой (ECDSS - Elliptic Curve Digital Signature Scheme), которая основана на применении эллиптических кривых, - их мы обсуждали в "B. Стандарты и организации по стандартизации" . Схема иногда упоминается как ECDSA (Elliptic Curve Digital Signature Algorithm). рис. 3.15 показывает общую идею ECDSS.
В процессе подписания две функции и экстрактор (извлекающее устройство) создают две подписи; в процессе проверки (верификации) обрабатывают выход одной функции (после прохождения через экстрактор) и сравнивают ее с первой подписью для проверки. Функции f1 и f3 фактически создают точки на кривой. Первая создает новую точку для секретного ключа подписывающего лица. Вторая - новую точку из двух общедоступных ключей подписывающего лица. Каждый экстрактор извлекает первые координаты соответствующей точки в модульной арифметике. Детали входов и функций коротко обсуждаются далее.
Генерация ключей
Генерация ключей осуществляется следующими шагами:
- Алиса выбирает эллиптическую кривую Ep (a,b) с простым числом p.
- Алиса выбирает другое простое число q, чтобы использовать для вычисления.
- Алиса выбирает секретный ключ d, целое число.
- Алиса выбирает точку на кривой e1(.,....)
- Алиса вычисляет e2 (..,....) = d x e1 (......), другую точку на кривой.
- Общедоступный ключ Алисы - (a, b, p, q, e1, e2), ее секретный ключ - d.
Подписание и проверка (верификация)
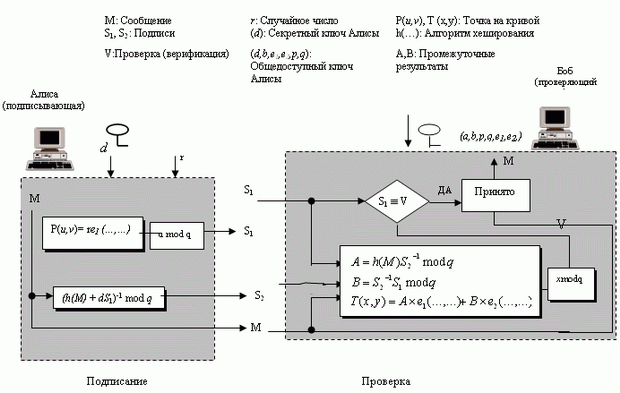
Рис. 3.16 показывает схему цифровой подписи эллиптической кривой.
Подписание. Процесс подписания состоит главным образом из выбора секретного случайного числа, создания третьей точки на кривой, вычисления двух подписей и передачи сообщения и подписей.
- Алиса выбирает секретное случайное число, r, между 1 и q - 1.
- Алиса выбирает третью точку на кривой, P (U, v) = r x e1 (......).
- Алиса использует первые координаты P (u, v), чтобы вычислить первую подпись S1 . Это означает S1 = u mod q.
- Алиса использует дайджест сообщения, свой секретный ключ и секретное случайное число r и S1, чтобы вычислить вторую подпись S2 = (h (M) + d x S1) r-1 mod q,
- Алиса передает М, S1 и S2.
Проверка (верификация).Процесс проверки состоит главным образом из восстановления третьей точки и подтверждения, что первая координата эквивалентна S1 по модулю q. Обратите внимание, что третья точка была создана подписывающим лицом, использующим секретное случайное число r. Верификатор не имеет этого значения. Ему нужно создать третью точку из дайджеста сообщения, S1 , и S2.
- Боб применяет М, S1 и S2 для создания двух промежуточных результатов A и B:
A = h(M)S2-1 mod q
B = S2-1S1 mod q
Затем Боб восстанавливает третью точку T(x,y) = A x e1( ... , ...) + B x e2( ... , ...)
- Боб использует первую координату из T(x,y), чтобы проверить сообщение. Если x = S1 mod q, подпись принимается, иначе - отклоняется.