|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Цифровая подпись
3.5. Схемы цифровой подписи
Несколько схем цифровой подписи были распространены в течение прошлых нескольких десятилетий. Некоторые из них были реализованы. В этой секции мы поговорим об этих схемах. В следующей секции мы обсуждаем одну, которая, вероятно, станет стандартом.
Схема цифровой подписи RSA
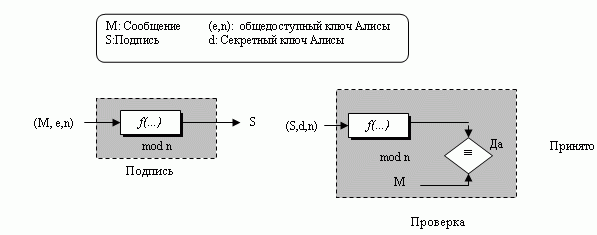
В "B. Стандарты и организации по стандартизации" мы обсуждали, как использовать криптографическую систему RSA для обеспечения секретности. Идея RSA может также применяться для того, чтобы подписать и подтвердить сообщение. В этом случае это называется схемой цифровой подписи RSA. Схема цифровой подписи меняет роли секретных и открытых ключей. Первое: используются секретный и открытый ключи передатчика, а не приемника. Второе: передатчик использует свой собственный секретный ключ для подписи документа; приемник использует открытый ключ передатчика, чтобы проверить этот документ. Если мы сравним схему с обычным способом подписи, мы видим, что секретный ключ играет роль передатчика собственной подписи, а открытый ключ - роль передатчика копии подписи, которая является общедоступной. Очевидно, Алиса не может использовать открытый ключ Боба, чтобы подписать сообщение, потому что тогда любой другой человек мог бы сделать то же самое. рис. 3.6 дает общую идею схемы цифровой подписи RSA.
Подписание и подтверждение сайтов используют ту же самую функцию, но с различными параметрами. Верификатор сравнивает сообщение и вывод функции для сравнения. Если результат истинен, сообщение принято.
Генерация ключей
Генерация ключей в схеме цифровой подписи RSА точно такая же, как и генерация ключей в криптографической системе RSА (см.
"B. Стандарты и организации по стандартизации"
). Алиса выбирает два простых числа p и q и вычисляет n = p x q. Алиса вычисляет  . Затем она выбирает e, для общедоступного ключа и вычисляет d для частного ключа, такое, что
. Затем она выбирает e, для общедоступного ключа и вычисляет d для частного ключа, такое, что  . Алиса сохраняет d и публично объявляет n и e.
. Алиса сохраняет d и публично объявляет n и e.
Подписание и проверка
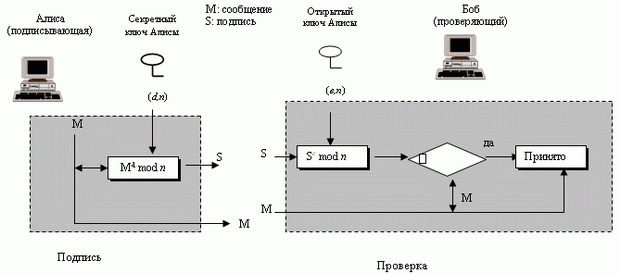
Рис 3.7 показывает схему цифровой подписи RSA.
Подписание. Алиса на основе сообщения создает подпись, используя частный (секретный) ключ, S = Md mod n, и передает сообщение и подпись Бобу.
Проверка. Боб получает М и S. Он применяет общедоступный ключ Алисы к подписи, чтобы создать копию сообщения М' = Se mod n. Боб сравнивает значение М' со значением М. Если два значения совпадают, Боб принимает сообщение. Чтобы доказать правильность этой процедуры, мы применяем критерии проверки:

Последняя конгруэнтность справедлива, потому что  (см. теорему Эйлера в
"A. ASCII"
).
(см. теорему Эйлера в
"A. ASCII"
).
Пример 3.1
Для безопасности подписи значения p и q должны быть очень большими. Как тривиальный пример, предположим, что Алиса выбирает p = 823 и q = 953 и вычисляет n = 784319. Значение  - 782544. Теперь она выбирает e = 313 и вычисляет d = 160009. В этой точке генерация ключей закончена. Теперь вообразим, что Алиса хочет передать сообщение со значением M = 19070 Бобу. Она использует свой частный ключ 160009 для того, чтобы подписать сообщение:
- 782544. Теперь она выбирает e = 313 и вычисляет d = 160009. В этой точке генерация ключей закончена. Теперь вообразим, что Алиса хочет передать сообщение со значением M = 19070 Бобу. Она использует свой частный ключ 160009 для того, чтобы подписать сообщение:
M = 19070 -> S = (19070160009) mod 784319 = 210625 mod 784319
Алиса передает сообщение и подпись Бобу. Боб получает сообщение и подпись. Он вычисляет

Боб принимает сообщение, потому что он проверил подпись Алисы.
Атаки подписи RSA
Есть некоторые атаки, к которым Ева может обратиться для подделки схемы цифровой подписи RSА Алисы.
Атака только на ключ. Ева имеет доступ только к открытому ключу Алисы, перехватывает пару ( М, S ) и пробует создать другое сообщение М.', такое, что М' = Se mod n. Эта проблема по сложности решения равна проблеме дискретного логарифма, которую мы рассмотрели в "A. ASCII" . Это - экзистенциальная подделка и обычно бесполезна для Евы.
Атака при известном сообщении. Здесь Ева использует мультипликативное свойство RSА. Предположим, что Ева перехватила две пары подписи сообщения - (M1, S1) и (M2, S2), которые используют один и тот же секретный ключ. Если М. = M1 x M2 mod n, тогда S. = S1 x S2 mod n. Это просто доказать, потому что мы имеем
S = S1 x S2 mod n = (M1d x M2d) mod n = (M1 x M2)d mod n = Md mod n
Ева может создать М. = M1 x M2 mod n и может создать S. = S1 x S2 mod n ; глупый Боб поверит, что S - подпись Алисы на сообщении М. Эта атака, которая называется иногда мультипликативной атакой, проводится очень просто. Однако это - экзистенциальная подделка так, как сообщение, М является произведением двух предыдущих сообщений, созданных Алисой, а не Евой; сообщение М. обычно бесполезно.
Атака по выбранному сообщению. Эта атака также использует мультипликативное свойство RSA. Ева может так или иначе попросить, чтобы Алиса подписала два законных сообщения М1 и М2. С помощью их она позже создает новое сообщение М. = M1 x M2 . Ева может позже утверждать, что Алиса подписала M. Такую атаку называют так же, как и предыдущую - мультипликативная атака. Это очень серьезная атака схемы цифровой подписи RSA, потому что это - селективная подделка. (Ева может перемножать М1 и М2, чтобы получить полезный M ).
Подпись RSA на дайджесте сообщения
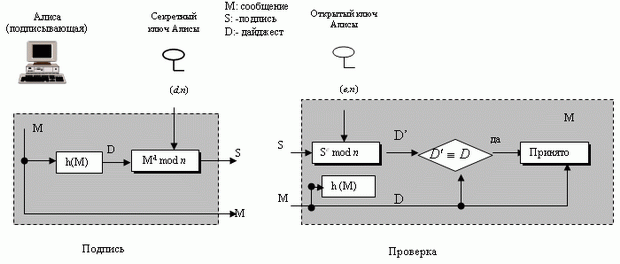
Как мы обсуждали прежде, подписание дайджеста сообщения и использование сильного алгоритма хэширования имеет несколько преимуществ. В случае RSA процессы подписания и проверки можно сделать намного быстрее, потому что схема цифровой подписи RSА - не что иное, как шифрование с секретным ключом и дешифрование с открытым ключом. Использование сильной графической функции хэширования также делает атаку подписи намного труднее, что мы коротко объясним. рис. 3.8 иллюстрирует схему.
Алиса, подписывающее лицо, при первом использовании согласует хэш-функцию, чтобы создать дайджест сообщения D = h(M). Затем она подписывает дайджест, S = Dd mod n. Сообщение и подпись передают Бобу. Боб, проверяющий, получает сообщение и подпись. Он сначала использует открытый ключ Алисы, чтобы извлечь (файл) дайджест, D' = Se mod n. Затем он применяет хэш-алгоритм для того, чтобы получить сообщение D = h(M).
Боб теперь сравнивает эти два дайджеста, D и D'. Если они являются сравнимыми по модулю n, он принимает сообщение.
Атаки на подписанные дайджесты RSA
Насколько восприимчива схема цифровой подписи RSA к нападению, когда дайджест уже подписан?
Атака только на ключ. Мы можем иметь три случая этой атаки.
- Ева перехватывает пару (S, M) и пробует найти другое сообщение М', которое создает тот же самый дайджест, h (M) = h (М'). Как мы узнали в "Целостность сообщения и установление подлинности сообщения" , если алгоритм хэширования обладает устойчивостью ко второму прообразу, эта атака очень трудна.
- Ева находит два сообщения, М. и М', такие, что h(M) = h(M'). Она соблазняет Алису подписать h(M), чтобы найти S ; теперь Ева имеет пару (М', S), которое прошло подтверждающий тест, но это - подделка. Мы изучали в "Целостность сообщения и установление подлинности сообщения" , что если алгоритм хэширования устойчив к коллизиям, эта атака очень трудна.
- Ева случайным подбором может найти дайджест сообщения D, который может соответствовать случайной подписи S. Она тогда находит сообщение М, такое, что D = h (M). Как мы узнали в "Целостность сообщения и установление подлинности сообщения" , если хэш-функция устойчива к прообразу, эта атака очень трудно осуществима.
Атака при известном сообщении. Предположим, что Ева имеет две пары подписи сообщения - (М1,S1) и (М2, S2), которые были созданы с использованием одного и того же секретного ключа. Ева вычисляет S = S1 x S2. Если она сможет найти сообщение М, такое, что h(M) = h(M1) x h(M2), она сможет подделать новое сообщение. Однако нахождение М по данному h (M) - это очень трудный процесс, если алгоритм хэширования устойчив к прообразу.
Атаки по выбранному сообщению. Ева может попросить, чтобы Алиса подписала два законных сообщения - М1,и М2 для нее. Она может создать новую подпись S = S1 x S2. Так как Ева может вычислить h(M) = h(M1) x h(M2), если она может найти сообщение M данному h (M), это новое сообщение - подделка. Однако нахождение М по данному h (M) -очень трудный процесс, если алгоритм хэширования устойчив к прообразу.