|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика временных рядов
10.2. Оценивание длины периода и периодической составляющей
Рассмотрим достаточно широкий класс практически полезных непараметрических оценок длины периода и периодической составляющей во временных рядах. Из общих результатов об асимптотическом поведении решений экстремальных статистических задач (см. "Оценивание" ) вытекает состоятельность этих оценок.
Во многих прикладных задачах рассматривают временной ряд (или случайный процесс)
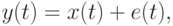
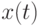 - детерминированная периодическая функция от времени
- детерминированная периодическая функция от времени  , т.е.
, т.е. 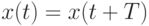 при некотором
при некотором  , где
, где  - длина периода (минимальная из возможных, поскольку
- длина периода (минимальная из возможных, поскольку 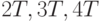 - тоже, как легко видеть, длины периодов), а
- тоже, как легко видеть, длины периодов), а  - "шумы", случайные погрешности, искажающие периодический сигнал. Требуется оценить (минимальную) длину периода
- "шумы", случайные погрешности, искажающие периодический сигнал. Требуется оценить (минимальную) длину периода 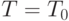 и периодическую составляющую
и периодическую составляющую 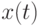 . При этом не предполагается, что функция
. При этом не предполагается, что функция 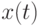 входит в какое-либо параметрическое семейство, например, конечных сумм синусов и косинусов, т.е. рассматривается задача непараметрического оценивания (минимальной) длины периода и периодической составляющей сигнала.
входит в какое-либо параметрическое семейство, например, конечных сумм синусов и косинусов, т.е. рассматривается задача непараметрического оценивания (минимальной) длины периода и периодической составляющей сигнала.Приведем примеры прикладных постановок.
- По акустическим сигналам необходимо установить тип двигателя (и его национальную принадлежность). Предполагается, что двигатели различаются по длине периода и виду основного периодического сигнала. Процедура идентификации основана на оценивании длины периода и периодической составляющей регистрируемого сигнала. Очевидна важность такой задачи при быстрой технической диагностике. В частности, высокая производительность, а потому и высокая экономическая эффективность при ремонте впрямую зависят от умения решать поставленную задачу. Не менее важно по шуму двигателя подводной лодки определить ее тип и национальную принадлежность.
- В предположении цикличности экономических процессов требуется по статистическим данным установить длину цикла и на основе вида периодической составляющей построить прогноз, например, прогноз урожайности, емкости рынка тех или иных товаров или экономической активности в целом. Часто говорят об экономических циклах, но почти никогда не дают строгого определения понятия цикла. (Под строгим определением понимаем такое, согласно которому можно отличить "цикл" от "не цикла", можно выделить начало и конец цикла, отделить один цикл от другого, короче, однозначно выделить цикл как самостоятельный объект экономического изучения.)
- По мнению авторов работы [ [ 10.24 ] ], для среднесрочного прогнозирования развития социокультурной сферы (социально-политического "климата", живописи, музыки, архитектуры, поэзии и т.д.) необходимо выявить ее цикличность с помощью объективных измерений на базе субъективных первичных данных (т.е. на базе оценок экспертов).
- В исторических событиях, описываемых согласно распространенной в настоящее время так называемой скалигеровской хронологии, автор работы [ [ 10.16 ] ] обнаруживает цикличность. Эта цикличность полностью объясняется новой статистической хронологией (см., например, [ [ 10.17 ] ]), построенной с помощью специальных методов статистики объектов нечисловой природы (см. "Статистика нечисловых данных" ), предназначенных для анализа текстов исторических хроник, и одновременно служит еще одним подтверждением этой хронологии.
Описание метода оценивания. Пусть рассматриваемые функции 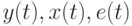 определены на отрезке
определены на отрезке ![[0; A]](/sites/default/files/tex_cache/850dc233b4cfde90739401b526d49e56.png) . При фиксированном
. При фиксированном  рассмотрим "куски" сигнала
рассмотрим "куски" сигнала  на последовательных отрезках длины
на последовательных отрезках длины  , т.е. на отрезках
, т.е. на отрезках ![[0;T], [T;2T], [2T;3T], ..](/sites/default/files/tex_cache/245b159f50c54a961bfccd935ecf6a2c.png) . Удобно ввести последовательность функций на отрезке
. Удобно ввести последовательность функций на отрезке ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) , полученную сдвигами этих кусков к началу координат:
, полученную сдвигами этих кусков к началу координат:
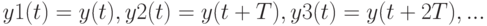
Все они определены на отрезке ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) . Число этих функций равно числу полных периодов длины
. Число этих функций равно числу полных периодов длины  , укладывающихся на отрезке
, укладывающихся на отрезке ![[0;A]](/sites/default/files/tex_cache/0efdd0915df68e29e2f8e78364fe1fb4.png) , т.е. равно целой части числа
, т.е. равно целой части числа 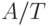 . Отметим еще раз, что если
. Отметим еще раз, что если  - период, то
- период, то 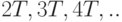 . - тоже периоды. В дальнейшем из всех периодов будем рассматривать и оценивать, как правило, только наименьший.
. - тоже периоды. В дальнейшем из всех периодов будем рассматривать и оценивать, как правило, только наименьший.
Если  - истинный период (или кратный ему) и погрешности
- истинный период (или кратный ему) и погрешности  отсутствуют, то все введенные в предыдущем абзаце функции совпадают между собой и с периодической составляющей:
отсутствуют, то все введенные в предыдущем абзаце функции совпадают между собой и с периодической составляющей:
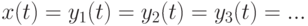
 из
из ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) . При наличии погрешностей полного совпадения не будет. Однако отклонения определяются лишь шумами в различные моменты времени. При этом в качестве оценки периодической составляющей
. При наличии погрешностей полного совпадения не будет. Однако отклонения определяются лишь шумами в различные моменты времени. При этом в качестве оценки периодической составляющей 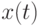 естественно взять среднее арифметическое
естественно взять среднее арифметическое 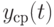 функций
функций 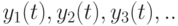 . (могут быть использованы и другие виды средних величин).
. (могут быть использованы и другие виды средних величин).Если же  отличается от истинного периода
отличается от истинного периода 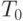 (и кратных ему величин), то различия функций
(и кратных ему величин), то различия функций 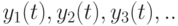 . между собой определяются также и различием значений
. между собой определяются также и различием значений 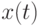 в точках, отстоящих друг от друга на интервалы, длина которых кратна
в точках, отстоящих друг от друга на интервалы, длина которых кратна  .
.
В предположении отсутствия погрешностей (т.е. когда  тождественно равно 0) рассмотрим поведение функции
тождественно равно 0) рассмотрим поведение функции 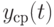 на отрезке
на отрезке ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) при росте длины интервала
при росте длины интервала  наблюдения сигнала, а потому и при росте числа периодов - целой части числа
наблюдения сигнала, а потому и при росте числа периодов - целой части числа 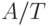 . Если
. Если 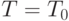 или
или  кратно
кратно 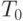 , то, как уже сказано,
, то, как уже сказано, 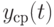 совпадает с периодической составляющей
совпадает с периодической составляющей 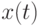 . Если число
. Если число 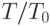 иррационально, то можно показать, что значения
иррационально, то можно показать, что значения 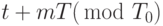 , где
, где  - натуральные числа такие, что
- натуральные числа такие, что 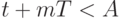 , асимптотически (при росте
, асимптотически (при росте  ) равномерно заполняют отрезок
) равномерно заполняют отрезок ![[0;T_0]](/sites/default/files/tex_cache/a943f7cee11f8b53c58e15eab526eb01.png) , а потому при выполнении соответствующих условий регулярности, например,
непрерывности периодической составляющей сигнала, функция
, а потому при выполнении соответствующих условий регулярности, например,
непрерывности периодической составляющей сигнала, функция 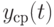 приближается к константе - среднему значению периодического сигнала
приближается к константе - среднему значению периодического сигнала 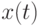 , т.е. интегралу от
, т.е. интегралу от 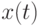 по отрезку
по отрезку ![[0;T_0]](/sites/default/files/tex_cache/a943f7cee11f8b53c58e15eab526eb01.png) , деленному на
, деленному на 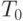 . При этом при конечных
. При этом при конечных  функция
функция 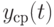 отлична от константы. (Здесь запись
отлична от константы. (Здесь запись 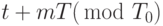 означает теоретико-числовое сравнение по модулю
означает теоретико-числовое сравнение по модулю 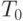 , т.е. взятие дробной части от числа
, т.е. взятие дробной части от числа 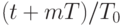 , что соответствует вычитанию соответствующего количества целых периодов
, что соответствует вычитанию соответствующего количества целых периодов 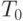 .
.
Если же число 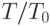 рационально, то наблюдаем промежуточный случай по сравнению с двумя описанными выше, в котором
рационально, то наблюдаем промежуточный случай по сравнению с двумя описанными выше, в котором 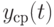 , как можно показать, приближается к периодической функции с периодом
, как можно показать, приближается к периодической функции с периодом 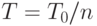 при некотором натуральном
при некотором натуральном  . Эта функция получена усреднением
. Эта функция получена усреднением  последовательных участков длины
последовательных участков длины 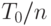 периодического сигнала
периодического сигнала 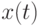 . Она не является константой, хотя разброс ее значений меньше, чем для исходного периодического сигнала, поскольку
. Она не является константой, хотя разброс ее значений меньше, чем для исходного периодического сигнала, поскольку 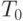 - минимальная длина периода.
- минимальная длина периода.
Из сказанного вытекает, что для оценивания  целесообразно ввести два показателя: показатель разброса
целесообразно ввести два показателя: показатель разброса 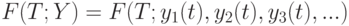 множества функций
множества функций 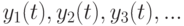 на отрезке
на отрезке ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) и показатель размаха
и показатель размаха  функции
функции 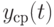 на отрезке
на отрезке ![[0;T]](/sites/default/files/tex_cache/75673c435e34622cdb42acb0a2bfdf8c.png) .
.
Символ  означает здесь, что показатели разброса и размаха строятся по функции
означает здесь, что показатели разброса и размаха строятся по функции 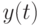 .) При этом показатель разброса нацелен на оценку различий в значениях семейства функций при одном и том же значении аргумента. А показатель размаха - на различие значений одной и той же функции при разных значениях аргумента. Ниже выписан ряд формул для этих показателей в случае непрерывного времени. Для дискретного времени их можно адаптировать двумя способами: либо заменив sup на max, а интеграл на сумму; либо расширив область определения используемых функций на весь отрезок, например, соединив соседние точки отрезками или использовав для заполнения пропусков сплайны более высокого порядка.
.) При этом показатель разброса нацелен на оценку различий в значениях семейства функций при одном и том же значении аргумента. А показатель размаха - на различие значений одной и той же функции при разных значениях аргумента. Ниже выписан ряд формул для этих показателей в случае непрерывного времени. Для дискретного времени их можно адаптировать двумя способами: либо заменив sup на max, а интеграл на сумму; либо расширив область определения используемых функций на весь отрезок, например, соединив соседние точки отрезками или использовав для заполнения пропусков сплайны более высокого порядка.
В качестве оценки длины периода по фиксированным показателям разброса 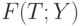 и размаха
и размаха 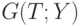 представляется рациональным использовать то
представляется рациональным использовать то  , при котором отношение
, при котором отношение 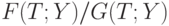 впервые (при росте
впервые (при росте  , начиная с 0) достигает минимума. Впервые - поскольку величины, кратные периоду, сами являются периодами. Поскольку показатели разброса
, начиная с 0) достигает минимума. Впервые - поскольку величины, кратные периоду, сами являются периодами. Поскольку показатели разброса 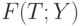 и размаха
и размаха 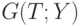 могут быть выбраны разными способами, можно указанным выше способом построить целое семейство алгоритмов оценивания длины периода, с каждым из которых может быть связано семейство методов оценивания периодической составляющей путем того или иного способа усреднения функций
могут быть выбраны разными способами, можно указанным выше способом построить целое семейство алгоритмов оценивания длины периода, с каждым из которых может быть связано семейство методов оценивания периодической составляющей путем того или иного способа усреднения функций 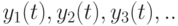 .
.
Показатели разброса и размаха. Ввести показатели разброса 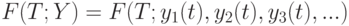 можно разными способами. Пусть
можно разными способами. Пусть ![k=[A/T]](/sites/default/files/tex_cache/6cbf238fce7c09004850aa9244cb98a2.png) . Можно использовать различные функционалы супремумного типа (здесь и далее число слагаемых k не будем указывать в обозначении функционалов). Первым рассмотрим максимальный разброс непосредственно между значениями функций:
. Можно использовать различные функционалы супремумного типа (здесь и далее число слагаемых k не будем указывать в обозначении функционалов). Первым рассмотрим максимальный разброс непосредственно между значениями функций:
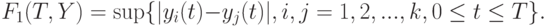
Второй функционал супремумного типа будет учитывать не произвольные отклонения, а только отклонения от "средней функции", т.е. иметь вид
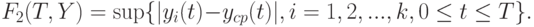
Третий функционал показывает, какую зону "заметают" значения функций:
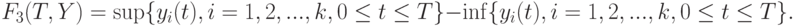
Для применения функционалов интегрального типа целесообразно сделать замену переменной 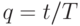 и перейти к функциям
и перейти к функциям 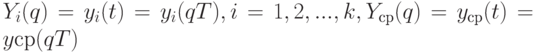 , определенным на отрезке [0;1]. В качестве показателя разброса представляется полезным рассмотреть то или иное отклонение совокупности функций
, определенным на отрезке [0;1]. В качестве показателя разброса представляется полезным рассмотреть то или иное отклонение совокупности функций 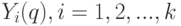 , друг относительно друга. Можно сказать, что эти функции заполняют некую "трубку", которая тоньше всего при истинном значении периода
, друг относительно друга. Можно сказать, что эти функции заполняют некую "трубку", которая тоньше всего при истинном значении периода  , а внутри нее проходит периодическая составляющая
, а внутри нее проходит периодическая составляющая  . Естественно рассмотреть различные функционалы интегрального типа. Например, можно проинтегрировать максимум модулей попарных разностей:
. Естественно рассмотреть различные функционалы интегрального типа. Например, можно проинтегрировать максимум модулей попарных разностей:
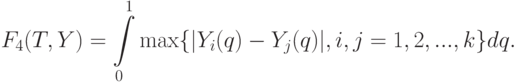
Вместо максимума можно проинтегрировать сумму:
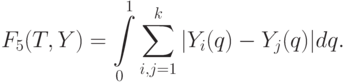
Как и для функционалов супремумного типа, естественно рассмотреть показатели разброса относительно "средней функции":
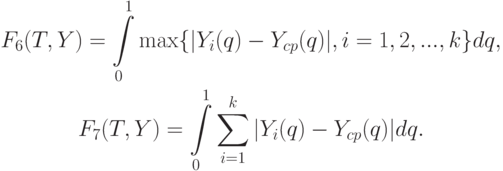
Следующие четыре функционала, используемые как показатели разброса, аналогичны четырем предыдущим, но включают в себя расчет квадратов:
![\begin{gathered}
F_8(T,Y)=\int\limits_0^1[\max\{|Y_i(q)-Y_j(q)|,i,j=1,2,...,k\}]^2 dq, \\
F_9(T,Y)=\int\limits_0^1\sum_{i,j=1}^k\{Y_i(q)-Y_j(q)\}^2 dq, \\
F_{10}(T,Y)=\int\limits_0^1[\max\{|Y_i(q)-Y_{cp}(q)|,i,j=1,2,...,k\}]^2 dq, \\
F_{11}(T,Y)=\int\limits_0^1\sum_{i=1}^k\{|Y_i(q)-Y_{cp}(q)|\}^2 dq.
\end{gathered}](/sites/default/files/tex_cache/5ac91d09e3756449631e4015279af3ba.png)
Список показателей разброса можно существенно расширить. В частности, естественно использовать также расстояния в функциональных пространствах 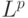 при произвольных
при произвольных 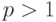 . А для оценивания периодической составляющей применять не только среднее арифметическое, но и другие виды средних величин.
. А для оценивания периодической составляющей применять не только среднее арифметическое, но и другие виды средних величин.
Показатели размаха также можно ввести самыми различными способами. Например, можно рассмотреть такой показатель:
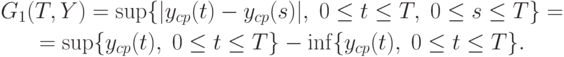
Пусть сделана замена переменной 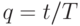 и осуществлен переход к функции
и осуществлен переход к функции 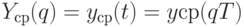 . Возможными показателями размаха являются:
. Возможными показателями размаха являются:
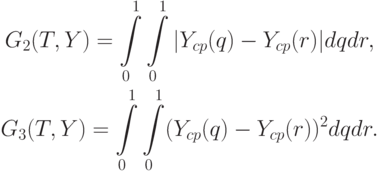
Введем среднее значение оценки периодической составляющей:
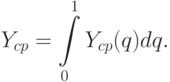
К естественным показателям размаха относятся, например, такие:
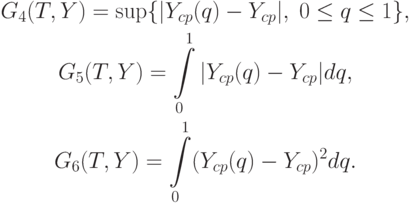
Список показателей размаха, как и список показателей разброса, можно значительно расширить. В частности, естественно использовать расстояния в функциональных пространствах 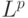 при произвольном
при произвольном  . А для оценивания периодической составляющей применять не только среднее арифметическое, но и другие виды средних - медиану, среднее геометрическое и др. Вопрос о выборе наилучших (в каком-либо смысле) показателей размаха и разброса здесь не обсуждается. Некоторые из причин этого отказа от оптимизации системы показателей рассмотрены ниже.
. А для оценивания периодической составляющей применять не только среднее арифметическое, но и другие виды средних - медиану, среднее геометрическое и др. Вопрос о выборе наилучших (в каком-либо смысле) показателей размаха и разброса здесь не обсуждается. Некоторые из причин этого отказа от оптимизации системы показателей рассмотрены ниже.
Алгоритмы оценивания. С прикладной точки зрения остается численно минимизировать один или несколько из 66 описанных выше функционалов 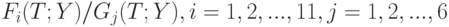 .
.
Численная минимизация по одному параметру (возможной длине периода) для современных ЭВМ не вызывает проблем, даже если попросту перебирать возможные значения периода с шагом 0,001. По нескольким реальным или смоделированным сигналам можно установить, какой из функционалов позволяет оценить период и периодическую составляющую реально встречающихся сигналов наиболее точно. Возможно и одновременное использование всех или части функционалов, что в соответствии с методологией устойчивости (см. "Теоретическая база прикладной статистики" ) позволяет установить чувствительность оценок к выбору метода оценивания, найти интервал их разброса. Проведенные в Институте высоких статистических технологий и эконометрики расчеты по реальным и смоделированным данным о временных рядах показали, что описанные выше алгоритмы позволяют оценивать длину периода и восстанавливать периодическую составляющую временного ряда достаточно точно с практической точки зрения.
В обширной литературе по временным рядам (см., например, монографии [ [ 2.6 ] , [ 10.8 ] , [ 2.15 ] ], дающие представление обо всем массиве литературы по этой тематике) проблеме оценивания периода не уделяется достаточного внимания. Фактически рекомендуют пользоваться либо периодограммой, либо автокорреляционной функцией. С помощью периодограммы (несостоятельной оценки спектральной плотности) можно выделить лишь синусоидальные составляющие, в то время как в кратко рассмотренных выше прикладных задачах периодическая составляющая представляет интерес сама по себе, без разложения на гармоники. Вторая рекомендация более полезна. В качестве оценки периода можно взять наименьшее положительное число, в котором достигается локальный максимум автокорреляционной функции. Эмпирический коэффициент автокорреляции - еще один функционал типа тех, что перечислены выше.
При поверхностном взгляде на проблемы статистического оценивания, как и на иные проблемы прикладной математики, часто возникает желание обсудить "оптимальность" тех или иных процедур. При более глубоком анализе становятся очевидными два обстоятельства. Во-первых, оптимальность имеет место лишь в рамках той или иной теоретической модели, при отклонениях от которой оптимальность оценки, как правило, пропадает. Например, выборочное среднее арифметическое как оценка математического ожидания случайной величины оптимальна тогда и только тогда, когда распределение результатов наблюдений - гауссово (доказательство этого утверждения приведено в монографии [ [ 10.6 ] ]). Во-вторых, для практически любой статистической процедуры можно подобрать свойство оптимальности так, чтобы эта процедура оказалась оптимальной (как подобрать - это уже дело профессионала). Так, например, метод наименьших модулей оптимален, если погрешности имеют распределение Лапласа, а метод наименьших квадратов - когда их распределение гауссово. Поскольку реальные распределения - не Лапласа и не Гаусса, то указанные математические результаты не могут иметь большого практического значения.
Однако представляется полезным получить доказательства состоятельности оценок изучаемых параметров в возможно более широких, например, непараметрических, постановках. Хотя на основе самого факта сходимости нельзя оценить близость оценок к интересующим исследователя параметрам, получение доказательства состоятельности - первый шаг при изучении скорости сходимости (см. 4.7).
Состоятельность оценок. Наиболее общий подход к установлению асимптотического поведения решений экстремальных статистических задач развит в статистике нечисловых данных для случая пространств произвольной природы (см.
"Оценивание"
). Согласно этому подходу сначала при фиксированном  доказывается сходимость (по вероятности) при
доказывается сходимость (по вероятности) при 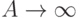 значений функционала (или показателей разброса и размаха) к некоторой предельной функции, а затем проверяются условия, обеспечивающие сходимость
значений функционала (или показателей разброса и размаха) к некоторой предельной функции, а затем проверяются условия, обеспечивающие сходимость  допредельного случайного процесса к
допредельного случайного процесса к  этой детерминированной функции.
этой детерминированной функции.
Свойства алгоритмов приходится изучать в рамках тех или иных вероятностно-статистических моделей. Моделей может быть много. Достаточно вспомнить историю Центральной предельной теоремы (ЦПТ) теории вероятностей. Она на протяжении более 200 лет доказывалась во все более и более широких условиях, вплоть до необходимых и достаточных условий Линдеберга-Феллера (после чего начались обобщения на зависимые слагаемые, на суммы случайных элементов гильбертовых пространств и др.). Отметим, что иногда математические модели далеко выходят за пределы, достаточные для обоснования алгоритмов анализа реальных данных. Так, почти всегда распределения реальных величин дискретны и финитны, а потому, в частности, существуют все моменты. Однако условия финитности и дискретности в вероятностно-статистических моделях часто необоснованно ослабляются. В результате возникают проблемы, не имеющие отношения к реальным данным, например, связанные с измеримостью относительно тех или иных сигма-алгебр. Поэтому ограничимся здесь наиболее простыми моделями из адекватных реальным постановкам. Считаем, что читатель знаком с основными определениями, относящимися к теории случайных процессов.
Теорема 1. Пусть случайный процесс  имеет нулевое математическое ожидание, является стационарным и эргодическим (т.е. выполнена теорема Биркгофа-Хинчина) с непрерывными траекториями. Тогда при фиксированном
имеет нулевое математическое ожидание, является стационарным и эргодическим (т.е. выполнена теорема Биркгофа-Хинчина) с непрерывными траекториями. Тогда при фиксированном  и
и 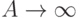 имеем
имеем
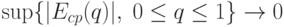
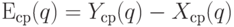 , т.е.
, т.е. 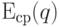 - среднее арифметическое погрешностей
- среднее арифметическое погрешностей 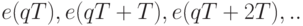 ..
..Доказательство теоремы 1 проводится стандартными методами теории стационарных временных рядов (с шагом  ) с использованием известного условия достаточно быстрого убывания элементов матрицы Лорана по мере удаления от ее главной диагонали (т.е. условия, необходимого и достаточного для справедливости теоремы Биркгофа-Хинчина). С помощью теоремы 1 можно найти асимптотику введенных выше показателей разброса и размаха.
) с использованием известного условия достаточно быстрого убывания элементов матрицы Лорана по мере удаления от ее главной диагонали (т.е. условия, необходимого и достаточного для справедливости теоремы Биркгофа-Хинчина). С помощью теоремы 1 можно найти асимптотику введенных выше показателей разброса и размаха.
Теорема 2. В предположениях теоремы 1 при фиксированном  и
и 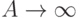 пронормированные показатели разброса
пронормированные показатели разброса 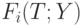 для наблюдаемого сигнала
для наблюдаемого сигнала  сближаются по распределению с соответствующими положительными случайными величинами
сближаются по распределению с соответствующими положительными случайными величинами 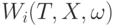 , зависящими от
, зависящими от  , характеристик случайного процесса
, характеристик случайного процесса  и периодической составляющей
и периодической составляющей  , т.е. существуют числовые последовательности
, т.е. существуют числовые последовательности 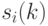 такие, что
такие, что
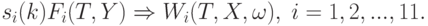
Доказательство теоремы 2 проводится с помощью достаточно трудоемких (в частности, из-за числа функционалов), но стандартных рассуждений. Они относятся к теории случайных процессов как части теории вероятностей. Эти рассуждения посвящены максимумам (не супремумам, так как траектории функции 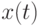 и случайного процесса
и случайного процесса  непрерывны) случайных процессов и интегралам от них, с использованием принципа инвариантности (см., например, учебное пособие [
[
4.1
]
]) и ряда результатов теории стационарных случайных процессов (см., например, монографию [
[
10.10
]
]). Таким образом, пронормированные функционалы разброса асимптотически не зависят от числа слагаемых - в этом и состоит основной смысл теоремы 2.
непрерывны) случайных процессов и интегралам от них, с использованием принципа инвариантности (см., например, учебное пособие [
[
4.1
]
]) и ряда результатов теории стационарных случайных процессов (см., например, монографию [
[
10.10
]
]). Таким образом, пронормированные функционалы разброса асимптотически не зависят от числа слагаемых - в этом и состоит основной смысл теоремы 2.
Теорема 3. В предположениях теоремы 1 при фиксированном  и
и 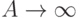 показатели размаха для наблюдаемого сигнала
показатели размаха для наблюдаемого сигнала  сближаются с соответствующими показателями для периодической составляющей
сближаются с соответствующими показателями для периодической составляющей  , т.е.
, т.е.

Для доказательства используются стандартные оценки, основанные на виде конкретных функционалов, задающих показатели размаха. В отличие от теоремы 2 предельные показатели детерминированы.
Аналоги теорем 2 и 3 верны также и при использовании (в качестве показателей разброса и размаха) расстояний в функциональных пространствах 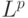 при произвольном
при произвольном 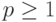 . А также при использовании для оценивания периодической составляющей не только среднего арифметического, но и других видов средних - медианы, среднего квадратического, среднего геометрического, обобщенных средних по Колмогорову (см.
"Описание данных"
) и др.
. А также при использовании для оценивания периодической составляющей не только среднего арифметического, но и других видов средних - медианы, среднего квадратического, среднего геометрического, обобщенных средних по Колмогорову (см.
"Описание данных"
) и др.
Теорема 4. Пусть выполнены условия теоремы 1, периодическая составляющая непрерывна и имеет период 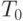 . Тогда при фиксированном
. Тогда при фиксированном  и
и 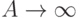 показатели разброса (пронормированные) и размаха стремятся к некоторым детерминированным пределам, зависящим только от
показатели разброса (пронормированные) и размаха стремятся к некоторым детерминированным пределам, зависящим только от  и
и 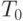 , т.е.
, т.е.

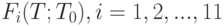 , и максимум каждой из функций
, и максимум каждой из функций 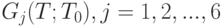 , достигается при
, достигается при  и при
и при  , кратных
, кратных 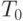 , причем у показателей разброса
, причем у показателей разброса 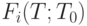 возможны и иные минимумы, а у показателей размаха
возможны и иные минимумы, а у показателей размаха 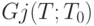 других максимумов нет.
других максимумов нет.Доказательство вытекает из теорем 2 и 3 и свойств усреднения периодической составляющей при росте длины интервала наблюдения сигнала, описанных ранее. Отметим, что предельные значения функционала разброса 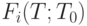 , вообще говоря, показывают разброс случайной погрешности, другими словами, не всегда зависят от периодической составляющей, а потому из-за нормировки на единичный отрезок в ряде случаев оказываются константами. Вместе с тем численные эксперименты показывают, что отмеченная сходимость к пределу является сравнительно медленной. И минимизация непосредственно функционалов разброса (без учета показателей размаха) при конкретной длине сигнала позволяет достаточно точно выделить периодическую составляющую из массива реальных данных. Однако описанные выше теоретические результаты заставили отказаться от первоначальной гипотезы о том, что достаточно использовать только показатели разброса, и привели к необходимости скорректировать алгоритмы, введя деление на показатели размаха.
, вообще говоря, показывают разброс случайной погрешности, другими словами, не всегда зависят от периодической составляющей, а потому из-за нормировки на единичный отрезок в ряде случаев оказываются константами. Вместе с тем численные эксперименты показывают, что отмеченная сходимость к пределу является сравнительно медленной. И минимизация непосредственно функционалов разброса (без учета показателей размаха) при конкретной длине сигнала позволяет достаточно точно выделить периодическую составляющую из массива реальных данных. Однако описанные выше теоретические результаты заставили отказаться от первоначальной гипотезы о том, что достаточно использовать только показатели разброса, и привели к необходимости скорректировать алгоритмы, введя деление на показатели размаха.
Теорема 5. В предположениях теоремы 4 оценки, являющиеся первыми локальными минимумами при минимизации по  отношений одного из 11 перечисленных выше показателей разброса к одному из 6 показателей размаха, являются состоятельными оценками истинного периода
отношений одного из 11 перечисленных выше показателей разброса к одному из 6 показателей размаха, являются состоятельными оценками истинного периода 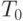 , а функция
, а функция 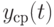 является состоятельной оценкой периодической составляющей
является состоятельной оценкой периодической составляющей 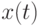 на отрезке
на отрезке ![[0;T_0]](/sites/default/files/tex_cache/a943f7cee11f8b53c58e15eab526eb01.png) .
.
Согласно теоремам 1-4 установлена сходимость (по вероятности) значений допредельных функционалов к предельным при каждом конкретном  . Поэтому для доказательства сходимости минимумов допредельных функционалов к минимумам предельных можно воспользоваться общей теорией асимптотического поведения решения экстремальных статистических задач. Условие асимптотической равномерной разбиваемости, сформулированное в работе [
[
1.17
]
], выполнено, как можно показать, в силу непрерывности траекторий случайного процесса (непрерывного сглаживания для временного ряда) и его периодической составляющей. Откуда и вытекает заключение теоремы 5, дающей теоретико-статистическое обоснование использованию системы описанных выше эвристических алгоритмов оценивания длины периода и периодической составляющей.
При известной или достаточно точно оцененной длине периода сама периодическая составляющая естественным образом оценивается с помощью усреднения перенесенных к началу координат кусков временного ряда, и в силу теоремы 1 эта оценка является состоятельной. Затем для получения оценки математического ожидания сигнала на всей области его определения указанную оценку можно периодически продолжить.
. Поэтому для доказательства сходимости минимумов допредельных функционалов к минимумам предельных можно воспользоваться общей теорией асимптотического поведения решения экстремальных статистических задач. Условие асимптотической равномерной разбиваемости, сформулированное в работе [
[
1.17
]
], выполнено, как можно показать, в силу непрерывности траекторий случайного процесса (непрерывного сглаживания для временного ряда) и его периодической составляющей. Откуда и вытекает заключение теоремы 5, дающей теоретико-статистическое обоснование использованию системы описанных выше эвристических алгоритмов оценивания длины периода и периодической составляющей.
При известной или достаточно точно оцененной длине периода сама периодическая составляющая естественным образом оценивается с помощью усреднения перенесенных к началу координат кусков временного ряда, и в силу теоремы 1 эта оценка является состоятельной. Затем для получения оценки математического ожидания сигнала на всей области его определения указанную оценку можно периодически продолжить.
Замечание. При практическом использовании рассматриваемых алгоритмов целесообразно учитывать дополнительные особенности реальных временных рядов. В частности, обратим внимание на неустойчивость супремумов по отношению к выбросам (резко выделяющимся наблюдениям) сравнительно с функционалами интегрального типа. Бывают ситуации, когда методики или аппаратура, регистрирующие значения реальных временных рядов, могут допускать сбои в отдельные моменты времени. Например, если происходит валютный кризис типа "черного вторника", когда курс доллара по отношению к рублю, строго говоря, не определен, другими словами - с точки зрения экономических агентов одновременно существует масса сильно отличающихся курсов. Аналогичная ситуация может возникнуть и в целом ряде других случаев. Набор подходящих ассоциаций вызывают решения руководства страны об обмене денежных знаков, особенно с дискриминационными составляющими. Во всех подобных ситуациях временные ряды дают резкие выбросы (всплески), которые затем, как правило, сглаживаются. Поэтому целесообразно в качестве показателей разброса и размаха использовать функционалы интегрального типа. Вопросам оценивания длины периода и периодической составляющей посвящены многие публикации, в том числе работа [ [ 10.21 ] ].
