|
Здравствуйте,ясдавала 15 тестов и экзамен. Мне нужно сейчас посмотреть результаты тестов.Как это сдлеать? |
Высказывания и предикаты
Информационно-логическая (инфологическая) задача – это задача, в которой необходимо установить некоторые информационные или логические связи и сделать необходимые причинно-следственные логические выводы. Эти задачи возникают в различных областях и часто являются плохо формализованными и структурированными. Их нужно хорошо формализовать и структурировать. Насколько хорошо будет возможно это сделать – настолько хорошо и полно будет решена рассматриваемая проблема или задача. Рассмотрим пример информационно-логической задачи (например, решаемой следователем, знакомым с алгеброй предикатов ).
Пример. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. В ходе следствия Браун сказал, что преступники были на синем "Бьюике", Джонс сказал, что это был черный "Крайслер", Смит утверждал, что это был "Форд", но не синий. Каждый указал неправильно либо марку, либо цвет автомобиля. Определим истинный цвет и истинную марку автомобиля. Рассмотрим простые высказывания вида: х = "машина – синяя", у = "машина – Бьюик", z = "машина – черная", u = "машина – Крайслер", v = "машина – Форд". На их основе высказывание Брауна можно записать в виде сложного логического выражения вида 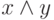 , высказывание Джонса – в виде
, высказывание Джонса – в виде 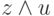 , а высказывание Смита – в виде
, а высказывание Смита – в виде  Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида:
Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида: 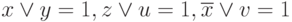 . По определению конъюнкции,
. По определению конъюнкции, 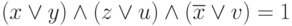 . Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение:
. Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение:
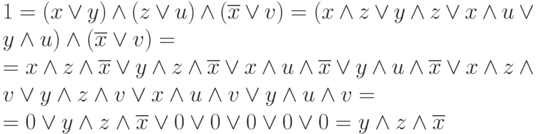
Мы использовали тот факт, что одновременно не могут быть истинными два высказывания относительно цвета или два высказывания относительно марки машины. Так как конъюнкция истинна только тогда, когда  , то заключаем, что автомобиль был черным "Бьюиком".
, то заключаем, что автомобиль был черным "Бьюиком".
Законы алгебры высказываний и предикатов сходны с правилами, по которым человек делает умозаключения, доказывает, мыслит.
Пример. Операции конъюнкции, дизъюнкции, отрицания алгебры высказываний – аналоги союзов "и", "или", приставки "не", используемых (возможно, интуитивно) при выражении мысли человеком.
Чтобы переложить на ЭВМ работы мыслительного характера, эти правила необходимо строго сформулировать, формализовать. Это позволяет осуществить алгебра логики. Приведем некоторые аксиомы логики – науки, изучающей методы доказательства и опровержения утверждений.
- Аксиома исключения третьего : либо имеет место высказывание, либо его отрицание.
- Аксиома противоречия : высказывания и его отрицание не могут иметь места одновременно.
- Аксиома двойного отрицания : двукратное отрицание какого-либо утверждения равносильно исходному утверждению.
- Аксиома тождества : всякое высказывание тождественно самому себе.
Если высказывания x и y связаны друг с другом отношением  , то говорят, что высказывание y следует из высказывания x (или y – следствие x ); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение
, то говорят, что высказывание y следует из высказывания x (или y – следствие x ); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение  – вывод.
– вывод.
Доказательство формальных математических утверждений (теорем) – последовательность корректных выводов, ведущих от условия к заключению. Алгебра логики помогает доказывать теоремы (дает общие подходы и методы доказательства).
Общий подход к доказательству теорем методом от противного, обратных и противоположных теорем можно формализовать с помощью алгебры логики.
