|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Задачи оптимизации при принятии решений
Линейное программирование
В теории принятия решений большое место занимают оптимизационные задачи Среди них наиболее известны задачи линейного программирования, в которых максимизируемая функция 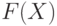 является линейной, а ограничения А задаются линейными неравенствами. Начнем с примера.
является линейной, а ограничения А задаются линейными неравенствами. Начнем с примера.
Производственная задача. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Изготовление стула требует 10 человеко-часов, стола - 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула - 45 долларов США, при производстве стола - 80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?
Обозначим:  - число изготовленных стульев,
- число изготовленных стульев, 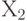 - число сделанных столов. Задача оптимизации имеет вид:
- число сделанных столов. Задача оптимизации имеет вид:

В первой строке выписана целевая функция - прибыль при выпуске  стульев и
стульев и 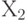 столов. Ее требуется максимизировать, выбирая оптимальные значения переменных
столов. Ее требуется максимизировать, выбирая оптимальные значения переменных  и
и 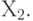 При этом должны быть выполнены ограничения по материалу (вторая строчка) - истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) - затрачено не более 450 часов. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если
При этом должны быть выполнены ограничения по материалу (вторая строчка) - истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) - затрачено не более 450 часов. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если  , то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то
, то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то  положительно. Но невозможно представить себе отрицательный выпуск -
положительно. Но невозможно представить себе отрицательный выпуск -  не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
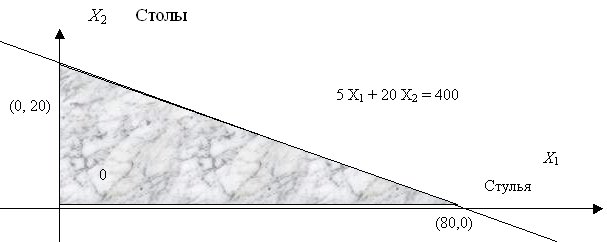
Условия производственной задачи можно изобразить на координатной плоскости. Будем по горизонтальной оси абсцисс откладывать значения  , а по вертикальной оси ординат - значения
, а по вертикальной оси ординат - значения 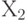 . Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения вектора
. Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения вектора 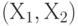 объемов выпуска в виде треугольника (рис. 8.1).
объемов выпуска в виде треугольника (рис. 8.1).
Таким образом, ограничения по материалу изображаются в виде выпуклого многоугольника, конкретно, треугольника. Этот треугольник получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей второй строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось  , соответствующую стульям, в точке (80, 0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось
, соответствующую стульям, в точке (80, 0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось 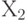 , соответствующую столам, в точке (0, 20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 столов. Для всех точек внутри треугольника выполнено неравенство, а не точное равенство - материал останется.
, соответствующую столам, в точке (0, 20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 столов. Для всех точек внутри треугольника выполнено неравенство, а не точное равенство - материал останется.
Аналогичным образом можно изобразить и ограничения по труду (рис. 8.2).
Таким образом, ограничения по труду, как и ограничения по материалу, изображаются в виде треугольника. Этот треугольник также получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей третьей строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось  , соответствующую стульям, в точке (45, 0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось
, соответствующую стульям, в точке (45, 0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось 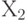 , соответствующую столам, в точке (0, 30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, а не точное равенство - часть рабочих будет простаивать.
, соответствующую столам, в точке (0, 30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, а не точное равенство - часть рабочих будет простаивать.
Мы видим, что очевидного решения нет - для изготовления 80 стульев есть материал, но не хватает рабочих рук, а для производства 30 столов есть рабочая сила, но нет материала, Значит, надо изготавливать и то, и другое. Но в каком соотношении?
Чтобы ответить на этот вопрос, надо "совместить" рис. 8.1 и рис. 8.2, получив область возможных решений, а затем проследить, какие значения принимает целевая функция на этом множестве (рис. 8.3).
Таким образом, множество возможных значений объемов выпуска стульев и столов 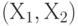 , или, в других терминах, множество А, задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис. 8.3. Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис. 8.1 и рис. 8.2, т.е. решение системы уравнений
, или, в других терминах, множество А, задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис. 8.3. Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис. 8.1 и рис. 8.2, т.е. решение системы уравнений
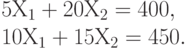
Из первого уравнения: 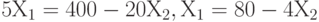 . Подставляем во второе уравнение:
. Подставляем во второе уравнение:
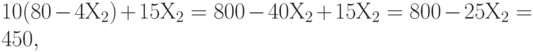
следовательно,  , откуда
, откуда  .
.
Итак, четвертая вершина четырехугольника - это (24, 14).
Надо найти максимум линейной функции на выпуклом многоугольнике. (В общем случае линейного программирования - максимум линейной функции на выпуклом многограннике, лежащем в конечномерном линейном пространстве.) Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. В общем случае - в одной вершине, и это - единственная точка максимума. В частном - в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.
Целевая функция  принимает минимальное значение, равное 0, в вершине (0, 0). При увеличении аргументов эта функция увеличивается. В вершине (24, 14) она принимает значение 2200. При этом прямая
принимает минимальное значение, равное 0, в вершине (0, 0). При увеличении аргументов эта функция увеличивается. В вершине (24, 14) она принимает значение 2200. При этом прямая 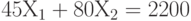 проходит между прямыми ограничений
проходит между прямыми ограничений  и
и  , пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24, 14).
, пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24, 14).
Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.
Двойственная задача. Каждой задаче линейного программирования соответствует так называемая двойственная задача. В ней по сравнению с исходной задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или, наоборот, вместо минимума - максимум). Задача, двойственная к двойственной - эта сама исходная задача. Сравним исходную задачу (слева) и двойственную к ней (справа):

Почему двойственная задача столь важна? Можно доказать, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной). При этом оптимальные значения  и
и 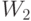 показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства,
показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства, 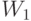 и
и 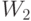 называют "объективно обусловленными оценками" сырья и рабочей силы.
называют "объективно обусловленными оценками" сырья и рабочей силы.
Линейное программирование как научно-практическая дисциплина. Из всех задач оптимизации задачи линейного программирования выделяются тем, что в них ограничения - системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны.
Впервые такие задачи решались советским математиком Л.В. Канторовичем (1912-1986) в 1930-х годах как задачи производственного менеджмента с целью оптимизации организации производства и производственных процессов, например, процессов загрузки станков и раскройки листов материалов. После второй мировой войны аналогичными задачами занялись в США. В 1975 г. Т. Купманс (1910-1985, родился в Нидерландах, работал в основном в США) и академик АН СССР Л.В. Канторович были награждены Нобелевскими премиями по экономике.
Рассмотрим несколько типовых задач линейного программирования .
Задача о диете (упрощенный вариант) . Предположим для определенности, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (для простоты, тиамина Т и ниацина Н).
| Содержание в 1 унции К | Содержание в 1 унции С | Потребность | |
|---|---|---|---|
| Вещество Т | 0,10 мг | 0,25 мг | 1,00 мг |
| Вещество Н | 1,00 мг | 0,25 мг | 5,00 мг |
| Калории | 110,00 | 120,00 | 400,00 |
| Стоимость 1 унции, в центах | 3,8 | 4,2 |
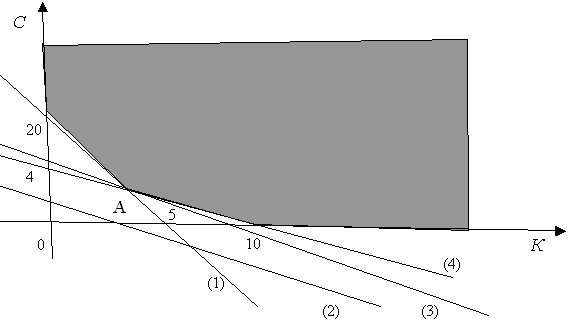
Пищевая ценность рациона (в калориях) должна быть не менее заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в табл. 8.1.
Задача линейного программирования имеет вид:
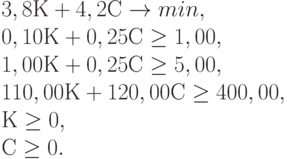
Ее графическое решение представлено на рис. 8.4