Некоторые определения теории графов
Перечисление деревьев
Теория перечисления графов занимается разработкой методов подсчета числа
неизоморфных графов, обладающих тем или иным свойством. Вероятнее всего,
эта теория возникла в 70-х годах девятнадцатого столетия и связана с
именем Кэли, который пытался найти число насыщенных углеводородов  , содержащих данное число атомов углерода.
Как он обнаружил,
эта задача сводится к подсчету числа деревьев, у которых степень каждой
вершины равна либо четырем, либо единице. Сейчас многие задачи по
перечислению графов решены.
, содержащих данное число атомов углерода.
Как он обнаружил,
эта задача сводится к подсчету числа деревьев, у которых степень каждой
вершины равна либо четырем, либо единице. Сейчас многие задачи по
перечислению графов решены.
Рассмотрим несколько определений
Помеченный граф с  вершинами — это граф, у
которого все вершины "помечены" целыми числами от 1 до
вершинами — это граф, у
которого все вершины "помечены" целыми числами от 1 до  . Более
точно, определим распределение меток в графе
. Более
точно, определим распределение меток в графе  с
с  вершинами как взаимно однозначное соответствие между множеством вершин
вершинами как взаимно однозначное соответствие между множеством вершин  и
множеством
и
множеством  ; тогда помеченным графом называется
пара
; тогда помеченным графом называется
пара 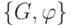 , где
, где  — граф, а
— граф, а  — распределение меток
в
— распределение меток
в  . Числа
. Числа 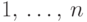 будем называть метками графа
будем называть метками графа  и обозначать вершины
и обозначать вершины  через
через 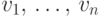 .
Назовем два помеченных графа
.
Назовем два помеченных графа  изоморфными, если существует изоморфизм между
изоморфными, если существует изоморфизм между  и
и 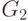 , сохраняющий распределение меток в этих графах.
, сохраняющий распределение меток в этих графах.
Пример. Различные распределения меток в дереве с четырьмя вершинами:
Внимательное изучение рисунка позволяет заметить, что второе помеченное
дерево является просто перевернутым первым, а отсюда следует, что эти два
помеченных дерева изоморфны. С другой стороны, ни одно из них не изоморфно
третьему помеченному дереву — достаточно посмотреть на степень
вершины 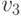 . Следовательно, общее число различных распределений
меток в данном дереве должно равняться
. Следовательно, общее число различных распределений
меток в данном дереве должно равняться 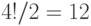 , поскольку
"переворот" любого распределения меток не приводит к новому объекту. Аналогично, общее
число различных распределений меток в дереве, изображенном на рисунке,
должно равняться четырем, так как его центральная вершина может быть
помечена четырьмя различными способами, каждый из которых однозначно
определяет распределение меток. Отсюда следует, что число всех
(неизоморфных) помеченных деревьев с четырьмя вершинами равно шестнадцати.
Рассмотрим теорему Кэли, обобщающую этот результат на помеченные деревья
с
, поскольку
"переворот" любого распределения меток не приводит к новому объекту. Аналогично, общее
число различных распределений меток в дереве, изображенном на рисунке,
должно равняться четырем, так как его центральная вершина может быть
помечена четырьмя различными способами, каждый из которых однозначно
определяет распределение меток. Отсюда следует, что число всех
(неизоморфных) помеченных деревьев с четырьмя вершинами равно шестнадцати.
Рассмотрим теорему Кэли, обобщающую этот результат на помеченные деревья
с  вершинами.
вершинами.
Теорема2.2(Кэли, 1889)
Существует ровно 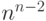 различных помеченных деревьев
с
различных помеченных деревьев
с  вершинами.
вершинами.
Доказательство теоремы: Moon J.W. Counting labeled trees, Canadi\-an Math. Congress, Montreal, 1970.

