Некоторые определения теории графов
Удаление ребер, мосты
При удалении ребра 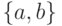 из графа
из графа  получается граф с теми же
вершинами, что и граф
получается граф с теми же
вершинами, что и граф  , и всеми ребрами, кроме ребра
, и всеми ребрами, кроме ребра 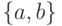 .
При удалении ребра из связного графа новый граф может оказаться как
связным, так и несвязным. Ребро
.
При удалении ребра из связного графа новый граф может оказаться как
связным, так и несвязным. Ребро 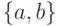 называется мостом
графа
называется мостом
графа  , если в графе, полученном после удаления из
, если в графе, полученном после удаления из  ребра
ребра 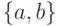 , вершины
, вершины  и
и  оказываются
несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может
заменить его определение, то есть по признаку можно распознать объект.
Рассмотрим признаки мостов.
оказываются
несвязными. Существует несколько признаков мостов. Известно, что признак какого-то объекта может
заменить его определение, то есть по признаку можно распознать объект.
Рассмотрим признаки мостов.
- Ребро
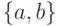 является мостом в том и только в том
случае, если
является мостом в том и только в том
случае, если 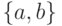 — единственный путь, соединяющий вершины
— единственный путь, соединяющий вершины  и
и  .
. - Ребро
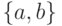 является мостом в том и только в том случае,
если найдутся две вершины
является мостом в том и только в том случае,
если найдутся две вершины  и
и  , такие, что каждый путь,
соединяющий их, содержит
, такие, что каждый путь,
соединяющий их, содержит  и
и  .
. - Ребро
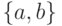 является мостом в том и только в том случае,
если оно не принадлежит ни одному циклу.
является мостом в том и только в том случае,
если оно не принадлежит ни одному циклу.
Докажем справедливость третьего признака.
Прямая теорема. Если ребро 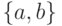 не принадлежит ни одному
циклу, то
не принадлежит ни одному
циклу, то 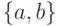 — мост.
— мост.
Так как ребро 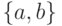 не принадлежит ни одному циклу, при его
удалении не останется пути, связывающего
не принадлежит ни одному циклу, при его
удалении не останется пути, связывающего  и
и  , то
есть
, то
есть 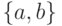 является мостом.
является мостом.
Обратная теорема.
Если ребро 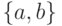 — мост, то
— мост, то 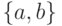 не принадлежит ни одному циклу.
не принадлежит ни одному циклу.
Если бы ребро 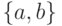 принадлежало циклу, то при удалении
ребра
принадлежало циклу, то при удалении
ребра 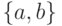 остался бы второй путь, связывающий
остался бы второй путь, связывающий  и
и  ,
то есть ребро
,
то есть ребро 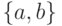 не было бы мостом.
Следовательно,
не было бы мостом.
Следовательно, 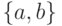 не принадлежит циклу.
не принадлежит циклу.
