Некоторые определения теории графов
Деревья
Связные графы, в которых существует одна и только одна цепь, соединяющая каждую пару вершин, называются деревьями. Дерево можно определить и как связный граф, не содержащий циклов.
Пример.
Кубок по настольному теннису разыгрывается по олимпийской системе. Встречи
проводятся без "ничьих". К очередному туру допускается только
победившая в
предыдущем туре команда. Проигравшие команды выбывают из игры. Для
завоевания кубка команда должна победить во всех турах. На участие
в розыгрыше кубка поданы заявки от 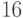 команд.
команд.
Схема проведения игр изображается графом
Вершины нижнего "яруса" дерева интерпретируем как команды,
участвующие в розыгрыше кубка, вершины второго снизу яруса — как команды-победительницы
в  финала, вершины третьего яруса — как
команды-победительницы
в
финала, вершины третьего яруса — как
команды-победительницы
в 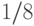 финала и т.д.
финала и т.д.
Какую информацию можно получить с помощью этого дерева?
Непосредственно с него считываются:
- Число всех участников розыгрыша кубка (число вершин нижнего "яруса").
- Число этапов проведения розыгрыша (число "ярусов" из вершин в дереве, не считая нижнего).
- Число команд, участвующих в
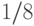 финала, в
финала, в 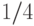 финала, в
финала, в 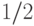 финала (число вершин, соответственно, в четвертом
сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе).
финала (число вершин, соответственно, в четвертом
сверху ярусе, в третьем сверху ярусе, во втором сверху ярусе). - Число матчей, которые придется сыграть командам для
выявления обладателя кубка (число вершин в графе без нижнего
"яруса"). Хотя это число легко определяется и без
дерева. (В каждом матче выбывает одна команда. Для того чтобы
была выявлена команда-победительница, остальные должны выбыть
из соревнования. Поэтому число матчей равно числу команд
без одной, а именно
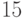 ).
).
Удобно считать, что граф, состоящий из одной изолированной вершины, тоже является деревом. Для каждой пары вершин дерева существует единственный соединяющий их путь. Лесом называется несвязный граф, представляющий объединение деревьев. Всякое ребро в дереве и в лесе является мостом (признак 3).
Пример.
Изображен лес, состоящий из четырех компонент, каждая из которых является деревом.
Заметим, что по определению деревья и леса являются простыми графами. По многим показателям дерево представляет собой простейший нетривиальный тип графа.
Известно, что в связном графе  удаление одного ребра,
принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа.
Применим эту процедуру к одному из оставшихся циклов, и так до тех пор,
пока не останется ни одного цикла. В результате получим дерево,
связывающее все вершины графа
удаление одного ребра,
принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа.
Применим эту процедуру к одному из оставшихся циклов, и так до тех пор,
пока не останется ни одного цикла. В результате получим дерево,
связывающее все вершины графа  , оно называется остовным
деревом или остовом, или каркасом графа
, оно называется остовным
деревом или остовом, или каркасом графа  .
.
В общем случае обозначим через  произвольный граф
с
произвольный граф
с  вершинами,
вершинами,  ребрами и
ребрами и  компонентами. Применяя описанную выше
процедуру к каждой компоненте
компонентами. Применяя описанную выше
процедуру к каждой компоненте  , получим в результате граф, называемый остовным лесом. Число удаленных в этой процедуре ребер называется циклическим рангом или циклическим числом
графа
, получим в результате граф, называемый остовным лесом. Число удаленных в этой процедуре ребер называется циклическим рангом или циклическим числом
графа  и
обозначается через
и
обозначается через  . Мы видим, что
. Мы видим, что  и является неотрицательным целым числом. Таким образом, циклический ранг
дает меру связности графа: циклический ранг дерева равен нулю, а
циклический ранг циклического графа равен единице. Удобно также определить
коциклический ранг или ранг разреза графа
и является неотрицательным целым числом. Таким образом, циклический ранг
дает меру связности графа: циклический ранг дерева равен нулю, а
циклический ранг циклического графа равен единице. Удобно также определить
коциклический ранг или ранг разреза графа  как число ребер в его
остовном лесе. Коциклический ранг обозначается через
как число ребер в его
остовном лесе. Коциклический ранг обозначается через  и
равен
и
равен 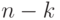 .
.
Теорема 2.1
Дерево с  вершинами имеет
вершинами имеет  ребро.
ребро.
Доказательство Для того чтобы из одного дерева  , не являющегося
изолированной вершиной, получить два дерева с теми же вершинами, необходимо удалить из
, не являющегося
изолированной вершиной, получить два дерева с теми же вершинами, необходимо удалить из  одно ребро. Для образования трех деревьев необходимо удалить
из
одно ребро. Для образования трех деревьев необходимо удалить
из  два каких-нибудь ребра. Самое большее, из дерева
два каких-нибудь ребра. Самое большее, из дерева  с
с  вершинами можно получить
вершинами можно получить  деревьев, каждое из которых является
изолированной вершиной. Для этого необходимо удалить
деревьев, каждое из которых является
изолированной вершиной. Для этого необходимо удалить  ребро из дерева
ребро из дерева  . Итак, действительно, в дереве с
. Итак, действительно, в дереве с  вершинами —
вершинами —  ребро.
ребро.


