Алгоритмы поиска в тексте
Алгоритм Бойера и Мура
Алгоритм Бойера и Мура считается наиболее быстрым среди алгоритмов, предназначенных для поиска подстроки в строке. Он был разработан Р. Бойером и Д. Муром в 1977 году. Преимущество этого алгоритма в том, что необходимо сделать некоторые предварительные вычисления над подстрокой, чтобы сравнение подстроки с исходной строкой осуществлять не во всех позициях – часть проверок пропускаются как заведомо не дающие результата.
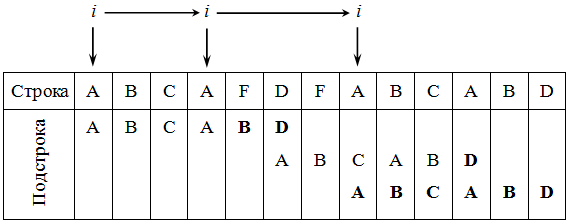
Существует множество вариаций алгоритма Бойера и Мура, рассмотрим простейший из них, который состоит из следующих шагов. Первоначально строится таблица смещений для искомой подстроки. Далее идет совмещение начала строки и подстроки и начинается проверка с последнего символа подстроки. Если последний символ подстроки и соответствующий ему при наложении символ строки не совпадают, подстрока сдвигается относительно строки на величину, полученную из таблицы смещений, и снова проводится сравнение, начиная с последнего символа подстроки. Если же символы совпадают, производится сравнение предпоследнего символа подстроки и т.д. Если все символы подстроки совпали с наложенными символами строки, значит, найдена подстрока и поиск окончен. Если же какой-то (не последний) символ подстроки не совпадает с соответствующим символом строки, далее производим сдвиг подстроки на один символ вправо и снова начинаем проверку с последнего символа. Весь алгоритм выполняется до тех пор, пока либо не будет найдено вхождение искомой подстроки, либо не будет достигнут конец строки ( рис. 39.3). На рисунке символы, подвергшиеся сравнению, выделены жирным шрифтом.
Величина сдвига в случае несовпадения последнего символа вычисляется, исходя из следующего: сдвиг подстроки должен быть минимальным, таким, чтобы не пропустить вхождение подстроки в строке. Если данный символ строки встречается в подстроке, то смещаем подстроку таким образом, чтобы символ строки совпал с самым правым вхождением этого символа в подстроке. Если же подстрока вообще не содержит этого символа, то сдвигаем подстроку на величину, равную ее длине, так что первый символ подстроки накладывается на следующий за проверявшимся символом строки.
Величина смещения для каждого символа подстроки зависит только от порядка символов в подстроке, поэтому смещения удобно вычислить заранее и хранить в виде одномерного массива, где каждому символу алфавита соответствует смещение относительно последнего символа подстроки.
//описание функции алгоритма Бойера и Мура
int BMSearch(char *string, char *substring){
int sl, ssl;
int res = -1;
sl = strlen(string);
ssl = strlen(substring);
if ( sl == 0 )
cout << "Неверно задана строка\n";
else if ( ssl == 0 )
cout << "Неверно задана подстрока\n";
else {
int i, Pos;
int BMT[256];
for ( i = 0; i < 256; i ++ )
BMT[i] = ssl;
for ( i = ssl-1; i >= 0; i-- )
if ( BMT[(short)(substring[i])] == ssl )
BMT[(short)(substring[i])] = ssl - i - 1;
Pos = ssl - 1;
while ( Pos < sl )
if ( substring[ssl - 1] != string[Pos] )
Pos = Pos + BMT[(short)(string[Pos])];
else
for ( i = ssl - 2; i >= 0; i-- ){
if ( substring[i] != string[Pos - ssl + i + 1] ) {
Pos += BMT[(short)(string[Pos - ssl + i + 1])] - 1;
break;
}
else
if ( i == 0 )
return Pos - ssl + 1;
cout << "\t" << i << endl;
}
}
return res;
}Алгоритм Бойера и Мура на хороших данных очень быстр, а вероятность появления плохих данных крайне мала. Поэтому он оптимален в большинстве случаев, когда нет возможности провести предварительную обработку текста, в котором проводится поиск. Таким образом, данный алгоритм является наиболее эффективным в обычных ситуациях, а его быстродействие повышается при увеличении подстроки или алфавита. В наихудшем случае трудоемкость рассматриваемого алгоритма O(m+n).
Существуют попытки совместить присущую алгоритму Кнута, Морриса и Пратта эффективность в "плохих" случаях и скорость алгоритма Бойера и Мура в "хороших" – например, турбо-алгоритм, обратный алгоритм Колусси и другие.
Каждый алгоритм поиска позволяет эффективно действовать лишь для своего класса задач, об этом еще говорят различные узконаправленные улучшения. Алгоритм поиска подстроки в строке следует выбирать только после точной постановки задачи, которые должна выполнять программа.
Ключевые термины
Алгоритм Бойера и Мура – это алгоритм поиска подстроки в строке, при котором первоначально строится таблица смещений для искомой подстроки, проверка начинается с последнего символа подстроки после совмещения начала строки и подстроки.
Алгоритм Кнута, Морриса и Пратта – это алгоритм поиска подстроки в строке, при котором сдвиг подстроки выполняется на некоторое переменное количество символов.
Алгоритм прямого поиска – это алгоритм поиска подстроки в строке, при котором происходит посимвольное сравнение строки с подстрокой.
Алфавит – конечное множество символов
Длина строки – количество символов в строке
Подстрока – это последовательность подряд идущих символов в строке.
Префикс – это подстрока, начинающаяся с первого символа строки.
Строка – это последовательность символов.
Суффикс – это подстрока, заканчивающаяся на последний символ строки.
Краткие итоги
- Задачи поиска слова в тексте используются в криптографии, различных разделах физики, сжатии данных, распознавании речи и других сферах человеческой деятельности.
- Основная идея алгоритма прямым поиском заключается в посимвольном сравнении строки с подстрокой.
- Алгоритм прямого поиска является малозатратным и не нуждается в предварительной обработке и в дополнительном пространстве.
- Алгоритм Кнута, Морриса и Пратта основывается на том, что после частичного совпадения начальной части подстроки с соответствующими символами строки можно, вычислить сведения, с помощью которых быстро продвинуться по строке.
- Трудоемкость алгоритма Кнута, Морриса и Пратта лучше, чем трудоемкость алгоритма прямого поиска.
- Особенность алгоритма Бойера и Мура заключается в предварительных вычислениях над подстрокой с целью сравнения подстроки с исходной строкой, осуществляемой не во всех позициях.
- Алгоритм Бойера и Мура оптимален в большинстве случаев, когда нет возможности провести предварительную обработку текста, в котором проводится поиск.