Алгоритмы рекуррентных соотношений
Линейные рекуррентные соотношения с постоянными коэффициентами
Для решения рекуррентных соотношений общих правил, вообще говоря, нет. Однако существует весьма часто встречающийся класс соотношений, решаемый единообразным методом. Это - рекуррентные соотношения вида
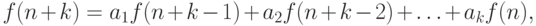 |
( 8.3) |
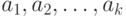 - некоторые числа. Такие соотношения
называют линейными
рекуррентными соотношениями с постоянными коэффициентами.
- некоторые числа. Такие соотношения
называют линейными
рекуррентными соотношениями с постоянными коэффициентами.Сначала рассмотрим, как решаются такие соотношения при  ,
то есть изучим соотношение вида
,
то есть изучим соотношение вида
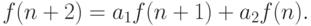 |
( 8.4) |
- Если
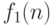 и
и 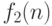 являются решениями
рекуррентного соотношения (8.4), то при любых числах
являются решениями
рекуррентного соотношения (8.4), то при любых числах  и
и  последовательность
последовательность 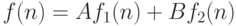 также является решением этого соотношения.
также является решением этого соотношения.В самом деле, по условию, имеем
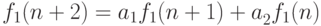
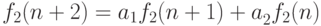
Умножим эти равенства на
 и
и  соответственно и
сложим полученные тождества. Получим, чтоА это означает, что
соответственно и
сложим полученные тождества. Получим, чтоА это означает, что![Af_1 (n + 2) + Bf_2 (n + 2) = a_1 [Af_1 (n + 1) + Bf_2 (n + 1)] +\\+ a_2 [Af_1
(n) + Bf_2 (n)].](/sites/default/files/tex_cache/89bc89feb4dc2ce4b0b5b571ac4332e2.png)
 является решением
соотношения(8.4).
является решением
соотношения(8.4).
- Если
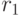 является корнем квадратного уравнениято последовательность
является корнем квадратного уравнениято последовательность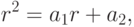 является решением рекуррентного соотношения
является решением рекуррентного соотношения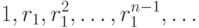 В самом деле, если
В самом деле, если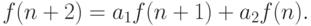
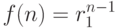 , то
, то 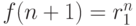 и
и 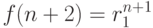 .
Подставляя эти значения в соотношение (8.4), получаем равенствоОно справедливо, так как по условию имеем
.
Подставляя эти значения в соотношение (8.4), получаем равенствоОно справедливо, так как по условию имеем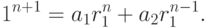
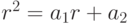 .
Заметим, что наряду с последовательностью
.
Заметим, что наряду с последовательностью 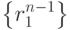 любая последовательность видатакже является решением соотношения (8.4). Для доказательства достаточно использовать утверждение (8.4), положив в нем
любая последовательность видатакже является решением соотношения (8.4). Для доказательства достаточно использовать утверждение (8.4), положив в нем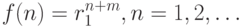
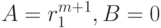 .
.
Из утверждений 1 и 2 вытекает следующее правило решения линейных рекуррентных соотношений второго порядка с постоянными коэффициентами.
Пусть дано рекуррентное соотношение
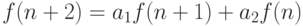 |
( 8.5) |
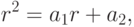 |
( 8.6) |
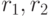 , то общее решение соотношения
(8.5) имеет вид
, то общее решение соотношения
(8.5) имеет вид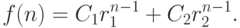
Чтобы доказать это правило, заметим сначала, что по утверждению 2 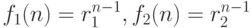 являются решениями нашего
соотношения. А тогда по утверждению 1 и
являются решениями нашего
соотношения. А тогда по утверждению 1 и 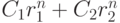 является его решением. Надо только показать,
что любое решение соотношения (8.5) можно записать в этом виде. Но любое решение
соотношения второго порядка определяется значениями
является его решением. Надо только показать,
что любое решение соотношения (8.5) можно записать в этом виде. Но любое решение
соотношения второго порядка определяется значениями 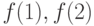 .
Поэтому достаточно показать, что система уравнений
.
Поэтому достаточно показать, что система уравнений
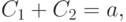
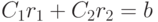
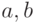 . Этими решениями являются
. Этими решениями являются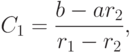
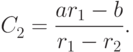
Пример на доказанное правило.
При изучении чисел Фибоначчи мы пришли к рекуррентному соотношению
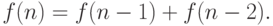 |
( 8.7) |
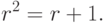
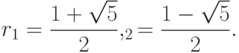
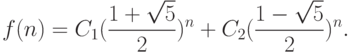 |
( 8.8) |
 вместо
вместо 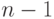 ). Мы называли числами Фибоначчи решения соотношения
(8.7), удовлетворяющее начальным условиям
). Мы называли числами Фибоначчи решения соотношения
(8.7), удовлетворяющее начальным условиям 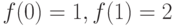 ( то есть
последовательность
( то есть
последовательность 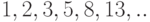 .). Часто бывает более удобно
добавить к этой последовательности вначале числа 0 и 1, то есть
рассматривать последовательность
.). Часто бывает более удобно
добавить к этой последовательности вначале числа 0 и 1, то есть
рассматривать последовательность 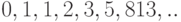 . Ясно, что эта
последовательность удовлетворяет тому же самому рекуррентному
соотношению (8.6) и начальным условиям
. Ясно, что эта
последовательность удовлетворяет тому же самому рекуррентному
соотношению (8.6) и начальным условиям 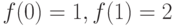 .
Полагая в формуле (8.8)
.
Полагая в формуле (8.8) 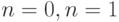 , получаем для
, получаем для 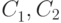 систему уравнений
систему уравнений
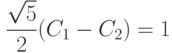
 и потому
и потому![f(n) = \frac{1}{\sqrt 5 }[(\frac{{1 + \sqrt 5 }}
{2})^n - (\frac{{1 - \sqrt 5 }}{2})^n ].](/sites/default/files/tex_cache/b7c01784a8ded68996d9bf30a1f541c1.png) |
( 8.9) |
 принимает целые значения.
принимает целые значения.