НОУ ИНТУИТ | Введение в схемы, автоматы и алгоритмы. Лекция 1: Предварительные сведения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 21.08.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Тверской государственный университет

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать программу

Формулы

Как мы видели, табличное представление булевых функций подходит лишь для функций с небольшим числом аргументов. Формулы позволяют удобно представлять многие функции от большего числа аргументов и оперировать различными представлениями одной и той же функции.

Мы будем рассматривать формулы, построенные над множеством элементарных функций 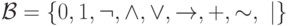$\mathcal{B}=\{ 0, 1, \neg, \wedge, \vee, \rightarrow, +, \sim,\ | \}$ . Все эти функции, кроме констант, называются логическими связками или логическими операциями. При этом для 2-местных функций из этого списка будем использовать инфиксную запись, в которой имя логической связки помещается между 1-ым и 2-ым аргументами.

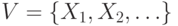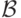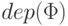Зафиксируем некоторое счетное множество переменных $V=\{ X_1, X_2, \ldots \}$ . Определим по индукции множество формул над $\mathcal{B}$ с переменными из . Одновременно будем определять числовую характеристику $dep(\Phi)$ формулы $\Phi$ , называемую ее глубиной, и множество ее подформул.

Определение 1.2. а) Базис индукции. 0, 1 и каждая переменная $X_i \in V$ является формулой глубины 0, т.е. . Множество ее подформул состоит из нее самой.

б) Шаг индукции. Пусть $\Phi_1$ и $\Phi_2$ - формулы, $\circ \in \{ \wedge, \vee, \rightarrow, +, \sim,\ | \}$ . Тогда выражения $\Phi= \neg \Phi_1$ и $\Phi= ( \Phi_1 \circ \Phi_2)$ являются формулами. При этом $dep(\neg \Phi_1)=1 + dep( \Phi_1)$ , а $dep((\Phi_1 \circ \Phi_2))=1 + \max\{dep( \Phi_1), dep( \Phi_2)\}$ . Множество подформул $\Phi$ включает саму формулу $\Phi$ и для $\Phi= \neg \Phi_1$ все подформулы формулы $\Phi_1$ , а для $\Phi= ( \Phi_1 \circ \Phi_2)$ все подформулы формул $\Phi_1$ и $\Phi_2$ .

Каждой формуле 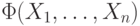$\Phi(X_1,\ldots, X_n)$ сопоставим булеву функцию, которую эта формула задает, используя индукцию по глубине формулы.

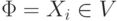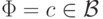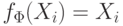Базис индукции. Пусть $dep(\Phi)=0$ . Тогда $\Phi = X_i \in V$ или $\Phi =c \in \mathcal{B}$ В первом случае $\Phi$ задает функцию $f_{\Phi}(X_i)=X_i$ , во втором - функцию, тождественно равную константе .

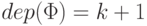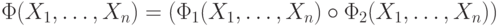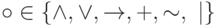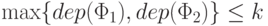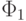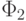Шаг индукции. Пусть $\Phi$ - произвольная формула глубины $dep(\Phi)= k+1$ . Тогда $\Phi(X_1,\ldots, X_n)= \neg \Phi_1(X_1,\ldots, X_n)$ или $\Phi(X_1,\ldots, X_n)= ( \Phi_1(X_1,\ldots, X_n) \circ \Phi_2(X_1,\ldots, X_n))$ для некоторой булевой связки $\circ \in \{ \wedge, \vee, \rightarrow, +, \sim,\ | \}$ . 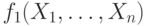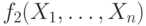Так как $\max \{dep( \Phi_1), dep( \Phi_2)\} \leq k$ , то формулам $\Phi_1$ и $\Phi_2$ соответствующие функции $f_1(X_1,\ldots, X_n)$ и $f_2(X_1,\ldots, X_n)$ уже сопоставлены. 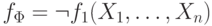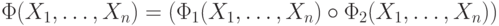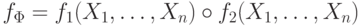Тогда формула $\neg\Phi_1$ задает функцию $f_{\Phi} =\neg f_1(X_1,\ldots, X_n)$ , а формула $\Phi(X_1,\ldots, X_n)= ( \Phi_1(X_1,\ldots, X_n) \circ \Phi_2(X_1,\ldots, X_n))$ задает функцию $f_{\Phi} = f_1(X_1,\ldots, X_n) \circ f_2(X_1,\ldots, X_n)$ .

Для определения функции, задаваемой небольшой формулой, удобно использовать таблицу, строки которой сответствуют наборам значений переменных, а в столбце под знаком каждой логической связки стоят значения функции, задаваемой соответствующей подформулой.

Пример 1.1. Например, для формулы

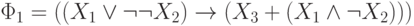
$\Phi_1= ( (X_1 \vee \neg\neg X_2)\rightarrow (X_3 + (X_1 \wedge \neg X_2)))$

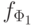функция $f_{\Phi_1}$ задается выделенным столбцом $\rightarrow$ следующей таблицы.

Таблица 1.3. Функция $f_{\Phi_1}$
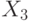
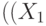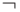
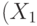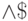	$\vee$ $\neg$ $\neg$	$\rightarrow$	$\wedge\$ $\neg$
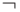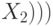
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 0 1 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 0 1 0 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1	1 1 0 1 1 0 0 1	0 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 0 0 0 1 0 1 1 1 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 1 1 0 0 1

Каждая строка этой таблицы задает процесс вычисления функции 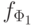$f_{\Phi_1}$ на соответствующих аргументах изнутри-наружу: вместо каждого вхождения переменной в формулу подставляется ее значение, затем в полученной формуле, состоящей из констант и булевых связок, последовательно вычисляются значения самых внутренних функций ( подформул ), для которых уже определены значения их аргументов, до тех пор, пока не будет получено значение всей формулы.

Дальше >>

Введение в схемы, автоматы и алгоритмы

Предварительные сведения

Формулы

Вопросы и ответы

Студенты

Авторизоваться

Введение в схемы, автоматы и алгоритмы

Предварительные сведения

Формулы

Вопросы и ответы

Студенты