|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Опубликован: 10.09.2004 | Уровень: для всех | Доступ: свободно | ВУЗ: Ульяновский государственный университет
Лекция 5:
Соединения и теоретико-множественные операции над отношениями
Аннотация: Рассматриваются специальные операции над отношениями: выборка, проекция, декартово произведение, соединение. Приводятся различные типы соединений: соединение по эквивалентности, естественное, внешнее соединение, полусоединение. Операции над отношениями иллюстрируются на примерах оператора SELECT. Рассматриваются примеры выбора данных из нескольких таблиц. Приводится объединение результатов нескольких запросов.
Ключевые слова: объединение отношений, пересечение, разность, декартово произведение, выборка, проекция, соединение, теоретико-множественные операции, операция проекции, операции реляционной алгебры, соединение по эквивалентности, внешнее соединение, полусоединение, кортеж отношения, деление
Рассмотрим основные операции над отношениями, которые могут представлять интерес с точки зрения извлечения данных из реляционных таблиц. Это объединение, пересечение, разность, расширенное декартово произведение отношений, а также специальные операции над отношениями: выборка, проекция и соединение.
Для иллюстрации теоретико-множественных операций над отношениями введем абстрактные отношения (таблицы) с некоторыми атрибутами (полями).
CREATE TABLE R (a1 CHAR(1), a2 INT, PRIMARY KEY(a1,a2))
CREATE TABLE S (b1 INT PRIMARY KEY, b2 CHAR(1))
Операции выборки и проекции являются унарными, поскольку они работают с одним отношением.
Операция выборки
Операция выборки - построение горизонтального подмножества, т.е. подмножества кортежей, обладающих заданными свойствами.
Операция выборки работает с одним отношением R и определяет результирующее отношение, которое содержит только те кортежи (строки) отношения R, которые удовлетворяют заданному условию F (предикату).
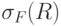или 
.
Пример 5.1. Операция выборки в SQL.
Выборка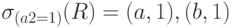 
записывается следующим образом:
SELECT a1, a2 FROM R WHERE a2=15.1. Операция выборки в SQL.
Операция проекции
Операция проекции - построение вертикального подмножества отношения, т.е. подмножества кортежей, получаемого выбором одних и исключением других атрибутов.
Операция проекции работает с одним отношением R и определяет новое отношение, которое содержит вертикальное подмножество отношения R, создаваемое посредством извлечения значений указанных атрибутов и исключения из результата строк-дубликатов.
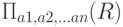
Пример 5.2. Операция проекции в SQL.
Проекция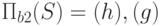 
записывается следующим образом:
SELECT DISTINCT b2 FROM S5.2. Операция проекции в SQL.
К основным операциям над отношениями относится декартово произведение.
Декартово произведение
Декартово произведение RxS двух отношений (двух таблиц) определяет новое отношение - результат конкатенации (т.е. сцепления) каждого кортежа (каждой записи) из отношения R с каждым кортежем (каждой записью) из отношения S .
RxS={(a, 1, 1, h), (a, 2, 1, h),
(b, 1, 1, h), ... }SELECT R.a1, R.a2, S.b1, S.b2 FROM R, S5.3. Декартово произведение отношений в SQL.
Результат декартова произведения двух отношений показан в таблице.
| R x S | |||
|---|---|---|---|
| R.a1 | R.a2 | S.b1 | S.b2 |
| a | 1 | 1 | h |
| a | 1 | 2 | g |
| a | 1 | 3 | h |
| a | 2 | 1 | h |
| a | 2 | 2 | g |
| a | 2 | 3 | h |
| b | 1 | 1 | h |
| b | 1 | 2 | g |
| b | 1 | 3 | h |
| b | 3 | 1 | h |
| b | 3 | 2 | g |
| b | 3 | 3 | h |
| b | 4 | 1 | h |
| b | 4 | 2 | g |
| b | 4 | 3 | h |
Если одно отношение имеет N записей и K полей, а другое M записей и L полей, то отношение с их декартовым произведением будет содержать NxM записей и K+L полей. Исходные отношения могут содержать поля с одинаковыми именами, тогда имена полей будут содержать названия таблиц в виде префиксов для обеспечения уникальности имен полей в отношении, полученном как результат выполнения декартова произведения.
Однако в таком виде (пример 5.3.) отношение содержит больше информации, чем обычно необходимо пользователю. Как правило, пользователей интересует лишь некоторая часть всех комбинаций записей в декартовом произведении, удовлетворяющая некоторому условию. Поэтому вместо декартова произведения обычно используется одна из самых важных операций реляционной алгебры - операция соединения, которая является производной от операции декартова произведения. С точки зрения эффективности реализации в реляционных СУБД эта операция - одна из самых трудных и часто входит в число основных причин, вызывающих свойственные всем реляционным системам проблемы с производительностью.
Федор Антонов
