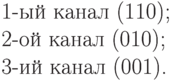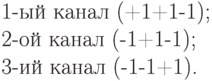Многостанционный доступ с кодовым разделением и сети CDMA
Неортогональные псевдослучайные функции
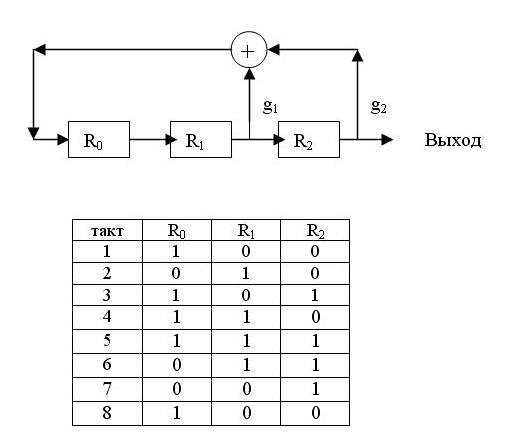
Неортогональные (асинхронные) псевдослучайные функции могут быть сгенерированы, используя сдвиговые регистры, сумматоры (сложение по модулю 2) и контуры обратной связи. рис. 7.4иллюстрирует такой принцип.
Максимальная длина последовательности определяется длиной регистра и конфигурацией цепи обратной связи (на рис. 7.4 цепи обратной связи обозначены 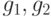 ). Регистр длиной
). Регистр длиной  битов может порождать свыше
битов может порождать свыше 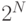 различных комбинации нулей и единиц. Так как цепь обратной связи выполняет линейные операции, то если все регистры будут иметь нулевое значение, то выход цепи обратной связи также будет нулевой. Поэтому, если установить все разряды на нуль то цепь обратной связи будет всегда давать нулевой выход для всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. Таким образом, максимальная длина любой последовательности равна
различных комбинации нулей и единиц. Так как цепь обратной связи выполняет линейные операции, то если все регистры будут иметь нулевое значение, то выход цепи обратной связи также будет нулевой. Поэтому, если установить все разряды на нуль то цепь обратной связи будет всегда давать нулевой выход для всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. Таким образом, максимальная длина любой последовательности равна 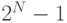 . Генерируемые последовательности называются последовательностями максимальной длины или m - последовательностями. Основное свойство таких последовательностей та, что автокорреляционная функция m - п
оследовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случаях. Это позволяет более четко выделять каналы. Конфигурации обратной связи для m-последовательности сведены в таблицу в
[
21
]
.
. Генерируемые последовательности называются последовательностями максимальной длины или m - последовательностями. Основное свойство таких последовательностей та, что автокорреляционная функция m - п
оследовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случаях. Это позволяет более четко выделять каналы. Конфигурации обратной связи для m-последовательности сведены в таблицу в
[
21
]
.
Последовательности, порождаемые регистрами сдвига, имеют еще много вариантов. В частности известны последовательности Голда, порождаемые совокупностью двух регистров. Последовательности Касами, порождаемые тремя регистрами и т.д. [ 21 ] .
Ортогональное расширение с использованием функций Уолша
Рассмотрим систему трех каналов, которая использует три ортогональных расширяющих последовательности, использующие ортогональные функции Уолша:
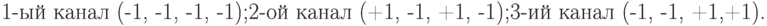
Предположим, что нам надо передать следующую информацию:
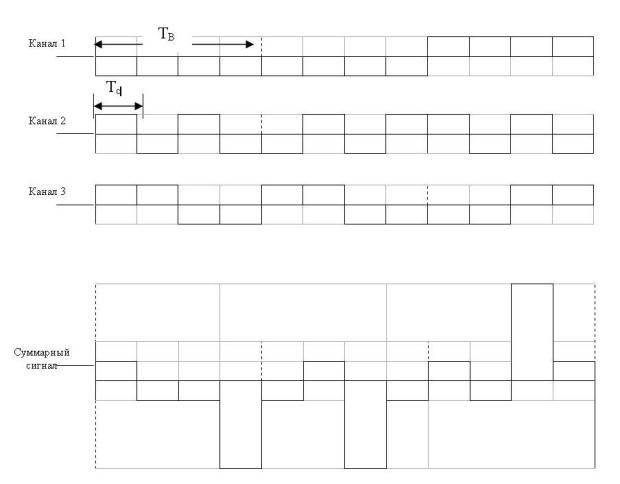
Комбинация расширяющей последовательности с информацией канала получается умножением всех разрядов последовательности на значение информационного бита. На рис. 7.5 показано получение такой последовательности для каждого из каналов. Это является аналогом частотной модуляции каналов.
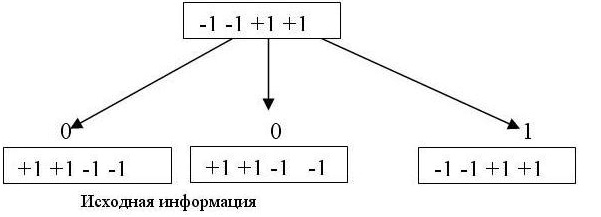
Рис. 7.5. Преобразование исходной информации для трех каналов с помощью ортогональных последовательностей Уолша
Теперь результаты расширения спектров каждого из каналов объединяются (суммируются), как это показано на рис. 7.6 и в табл. 7.3
| Каналы | Исходная информация | Последовательности расширенного спектра | ||
|---|---|---|---|---|
| Канал 1 | 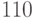 |
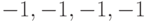 |
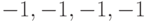 |
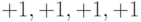 |
| Канал 2 | 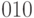 |
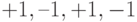 |
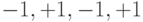 |
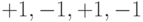 |
| Канал3 | 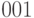 |
 |
 |
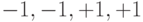 |
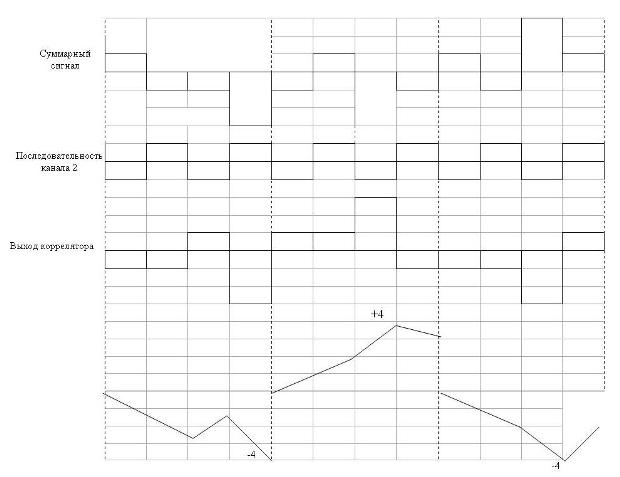
На рис.7.7 и в табл.7.4 показан пример восстановления первоначального сигнала с использованием ортогональных функций для канала 2.
увеличить изображение
Рис. 7.7. Пример восстановления первоначального сигнала с использованием ортогональных функций.
| Суммарный сигнал | 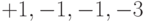 |
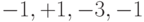 |
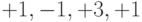 |
|---|---|---|---|
| Последовательность канала 2 | 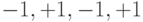 |
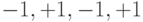 |
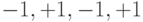 |
| Выход коррелятора | 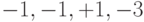 |
 |
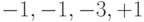 |
| Выход интегратора |  |
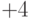 |
 |
| Двоичный выход |  |
 |
 |
Для восстановления исходного сигнала каждый разряд суммарного сигнала умножается на соответствующий разряд расширяющей последовательности канала 2. После чего полученные результаты суммируются в пределах одного периода последовательности. Каждый интегральный сигнал дает максимальное значение равное либо 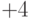 , либо
, либо 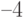 . В зависимости от этого исходный символ будет соответственно
. В зависимости от этого исходный символ будет соответственно 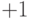 или
или 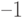 . Аналогично могут быть получены значения исходной последовательности в канале1 и 3. Если попытаться восстановить сигнал с использованием ортогональной последовательности не входящей в суммарный сигнал, то получается ноль для каждого периода интеграции.
. Аналогично могут быть получены значения исходной последовательности в канале1 и 3. Если попытаться восстановить сигнал с использованием ортогональной последовательности не входящей в суммарный сигнал, то получается ноль для каждого периода интеграции.
| Суммарный сигнал | 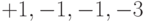 |
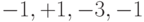 |
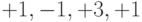 |
|---|---|---|---|
| Последовательность канала 3 | 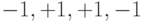 |
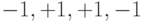 |
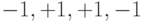 |
| Выход коррелятора | 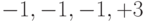 |
 |
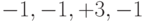 |
| Выход интегратора |  |
 |
 |
| Двоичный выход |  |
 |
 |
В заключение этого раздела приведем некоторые определения, которые применяются в системах CDMA
Длительность тактового интервала одного бита расширяющего сигнала называются чипами. Интервал 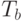 представляет период одного информационного разряда, и
представляет период одного информационного разряда, и 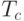 представляет период одного чипа (см. рис.7.6). Чиповая скорость(chip rate)
представляет период одного чипа (см. рис.7.6). Чиповая скорость(chip rate) 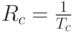 , часто используется, чтобы характеризовать систему передачи с широким спектром и обычно измеряется в Мчип/c.
, часто используется, чтобы характеризовать систему передачи с широким спектром и обычно измеряется в Мчип/c.
База сигнала (processing gain-PG) или иногда называемая коэффициент расширения спектра (spreading factor- SF)определяется как отношение чиповой скорости (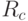 ) к скорости передачи информации (
) к скорости передачи информации (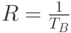 ).
).
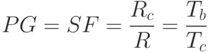
Это равенство представляет число чипов, содержащихся в одном информационном разряде. Чем выше значение базы сигнала (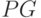 ), тем больше расширение. Высокий
), тем больше расширение. Высокий 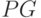 также означает что, больше кодов может быть распределено на том же самом частотном канале.
также означает что, больше кодов может быть распределено на том же самом частотном канале.