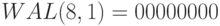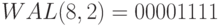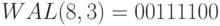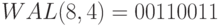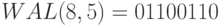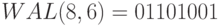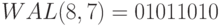Многостанционный доступ с кодовым разделением и сети CDMA
Корреляция и ортогональные функции Уолша
Как было сказано выше для объединения нескольких каналов при кодовом разделении каналов необходимо, чтобы псевдослучайные коды были, разделимы с помощью корреляционного фильтра. Для этого они должны достаточно различаться. Степень подобия (похожести) функций в математике отображается с помощью корреляции. Различаются взаимная корреляция - сравнение двух функций, ортогональная корреляция - при полной независимости двух функций и автокорреляция - сравнение функции с собой при сдвиге во времени.
- Взаимная корреляция (cross correlation) для двух периодических функций с периодом
 измеряет подобие двух сигналов сдвинутых во времени и определяется формулой
измеряет подобие двух сигналов сдвинутых во времени и определяется формулой
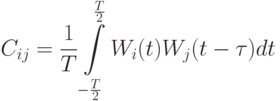
- Ортогональная корреляция – это частный случай взаимной корреляции, когда эта функция равна нулю. Эти сигналы могут передаваться одновременно, поскольку они не создают взаимных помех.
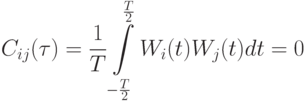
- Автокорреляция – периодического сигнала определяет подобие данной функции с ее же версией сдвинутой во времени и определяется следующей формулой
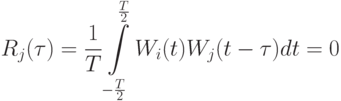
Для дискретных функций интегрирование можно заменить суммированием. В системах многостанционного доступа с кодовым разделением каналов применяются ортогональные функции Уолша. Одним из необходимых, (но не достаточных) свойств такого кода является его сбалансированность, т.е. одинаковое число нулей и единиц.
Ниже (
таблица
7.2)показаны ортогональные функции Уолша длины 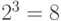 [
2
]
,
[
20
]
,
[
46
]
.
[
2
]
,
[
20
]
,
[
46
]
.
Заметим, что при кодировании обычно символ  заменяется
заменяется 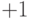 , а
, а  на
на 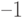 .
.
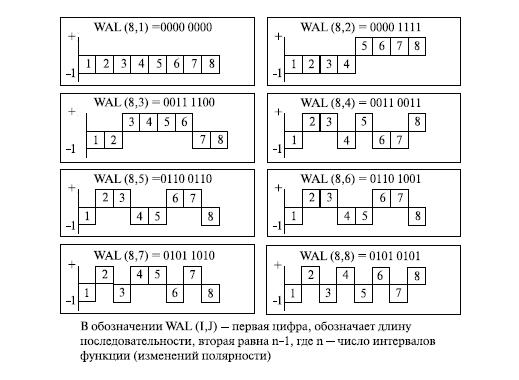
В обозначении 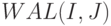 – первая цифра, обозначает длину последовательности, вторая равна
– первая цифра, обозначает длину последовательности, вторая равна  , где
, где  – число интервалов функции (изменений полярности). На рис. 7.3 приведены диаграммы соответствующие этим последовательностям.
– число интервалов функции (изменений полярности). На рис. 7.3 приведены диаграммы соответствующие этим последовательностям.
Ортогональные функции Уолша могут быть сгенерированы, с использованием итерационного процесса построения матрицы Адамара
[
20
]
. Начиная с ![H_1 = [0]](/sites/default/files/tex_cache/1b634d4ef6dd3e5093c010ba8638429f.png) . Матрица Адамара сформирована:
. Матрица Адамара сформирована:
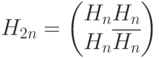
Коды Уолша - Адамара длины 2 и 4 будут получены соответственно:
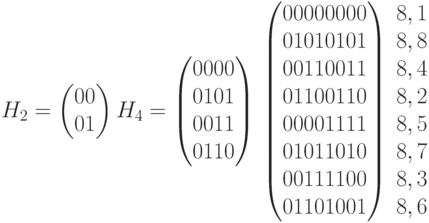
Полученная матрица с точностью до порядка следования совпадает с ортогональными функциями, приведенными в табл. 7.2. Для того чтобы облегчить сравнение, справа от матрицы приведены номера функций по табл. 7.2. и диаграмме рис. 7.3 .
Рассмотрим пример вычисления ортогональности полученных функций, Посмотрим взаимную корреляцию (без сдвига) функций  и
и 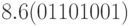 .
.
![[(-1)\times(-1)]+[(1\times 1)]+[(-1)\times 1]+[1\times(-1)] +[(-1)\times 1]+[1\times(-1)]+[(-1)\times(-1)]+[(1\times 1)]=0\\
\text{\qquad\quad 1 \qquad\qquad\quad 2 \qquad\qquad\quad 3 \qquad\quad\; 4 \qquad\qquad\qquad 5 \qquad\quad\; 6 \qquad\qquad\qquad 7 \qquad\qquad\quad 8}](/sites/default/files/tex_cache/520712f20e745dcd9fefa4988003df64.png)
Согласно полученному результату эти две функции ортогональны. Однако ортогональные функции Уолша имеют недостатки. Система должна быть синхронизирована. При сдвиге синхронизации функции корреляция увеличивается.
Для сдвинутых по времени и не синхронизированных сигналов, взаимная корреляция может быть, не равна нулю. Они могут интерферировать друг с другом. Вот почему, кодирование с помощью функций Уолша может только использоваться при синхронном CDMA.