Процедура обратного распространения (описание алгоритма)
Подстройка весов
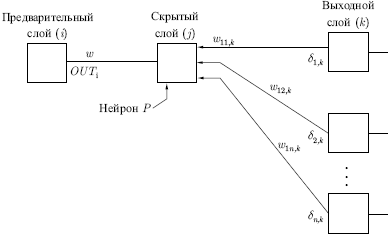
скрытого слоя. Рассмотрим один нейрон в
скрытом слое, предшествующем выходному слою. При проходе вперед этот
нейрон передает свой выходной сигнал нейронам в выходном слое через
соединяющие их веса. Во время обучения эти веса функционируют в
обратном порядке, пропуская величину  от выходного слоя
назад к
скрытому слою. Каждый из этих весов умножается на величину
от выходного слоя
назад к
скрытому слою. Каждый из этих весов умножается на величину  нейрона, к которому он присоединен в выходном слое. Величина
нейрона, к которому он присоединен в выходном слое. Величина  ,
необходимая для нейрона скрытого слоя, получается суммированием всех
таких произведений и умножением на производную сжимающей функции
(см. рис. 4.4):
,
необходимая для нейрона скрытого слоя, получается суммированием всех
таких произведений и умножением на производную сжимающей функции
(см. рис. 4.4):
![\delta_{q,k}=OUT_{p,j}(1-OUT_{p,j})\left[\sum_q\delta_{q,k}
w_{pq,k}\right].
\vspace{-2mm}](/sites/default/files/tex_cache/64086a97509451a2bdf2bcfe3182e240.png) |
( 7) |
Когда значение  получено, веса, питающие первый скрытый
уровень,
могут быть подкорректированы с помощью уравнений (5) и (6), где индексы
модифицируются в соответствии со слоем.
получено, веса, питающие первый скрытый
уровень,
могут быть подкорректированы с помощью уравнений (5) и (6), где индексы
модифицируются в соответствии со слоем.
Для каждого нейрона в данном скрытом слое должно быть вычислено  и подстроены все веса, ассоциированные с этим слоем. Этот
процесс
повторяется слой за слоем по направлению к входу, пока все веса не будут
подкорректированы.
и подстроены все веса, ассоциированные с этим слоем. Этот
процесс
повторяется слой за слоем по направлению к входу, пока все веса не будут
подкорректированы.
С помощью векторных обозначений операция обратного распространения ошибки
может быть записана значительно компактнее. Обозначим множество величин  выходного слоя через
выходного слоя через 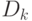 и множество весов
выходного слоя как массив
и множество весов
выходного слоя как массив  Чтобы получить
Чтобы получить 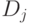 ,
,  -вектор выходного слоя, достаточно следующих двух операций:
-вектор выходного слоя, достаточно следующих двух операций:
- Умножить о-вектор выходного слоя
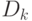 на транспонированную
матрицу весов
на транспонированную
матрицу весов 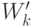 , соединяющую скрытый уровень с выходным
уровнем.
, соединяющую скрытый уровень с выходным
уровнем. - Умножить каждую компоненту полученного произведения на производную сжимающей функции соответствующего нейрона в скрытом слое.
Добавление
нейронного смещения. Во многих случаях желательно наделять каждый
нейрон обучаемым смещением. Это позволяет сдвигать начало отсчета
логистической функции, давая эффект, аналогичный
подстройке порога персептронного нейрона, и приводит к ускорению процесса
обучения. Такая возможность может быть легко введена в обучающий
алгоритм с помощью добавляемого к каждому нейрону веса, который присоединен к  Этот вес обучается так же, как и все остальные веса, за
исключением того, что подаваемый на него сигнал всегда равен
Этот вес обучается так же, как и все остальные веса, за
исключением того, что подаваемый на него сигнал всегда равен 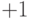 ,
а не выходу нейрона предыдущего слоя.
,
а не выходу нейрона предыдущего слоя.
Импульс. Существует метод ускорения обучения для алгоритма обратного распространения, увеличивающий также устойчивость процесса. Этот метод, названный импульсом, заключается в добавлении к коррекции веса члена, пропорционального величине предыдущего изменения веса. Как только происходит коррекция, она "запоминается" и служит для модификации всех последующих коррекций. Уравнения коррекции модифицируются следующим образом:
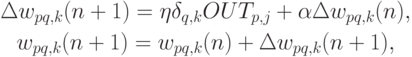
где  — коэффициент импульса, который обычно
устанавливается около 0,9.
— коэффициент импульса, который обычно
устанавливается около 0,9.
Используя метод импульса, сеть стремится идти по дну "узких оврагов" поверхности ошибки (если таковые имеются), а не двигаться "от склона к склону". Этот метод, по-видимому, хорошо работает на некоторых задачах, но дает слабый или даже отрицательный эффект на других.
Существует сходный метод, основанный на экспоненциальном сглаживании, который может иметь преимущество в ряде приложений.

Затем вычисляется изменение веса

где  — коэффициент сглаживания, варьируемый в диапазоне
от 0,0
до 1,0. Если
— коэффициент сглаживания, варьируемый в диапазоне
от 0,0
до 1,0. Если  равен 1,0, то новая коррекция игнорируется и
повторяется предыдущая. В области между 0 и 1 коррекция веса сглаживается
величиной, пропорциональной
равен 1,0, то новая коррекция игнорируется и
повторяется предыдущая. В области между 0 и 1 коррекция веса сглаживается
величиной, пропорциональной  По-прежнему,
По-прежнему,  является коэффициентом скорости обучения, служащим для
управления средней величиной изменения веса.
является коэффициентом скорости обучения, служащим для
управления средней величиной изменения веса.