Цвет в компьютерной графике

Цветовые модели HSV и HLS

Приведенные модели не охватывают всего диапазона видимого цвета, поскольку их цветовой охват - это лишь треугольник на графике МКО, вершинам которого соответствуют базовые цвета. Они являются аппаратно ориентированными, т.е. соответствуют технической реализации цвета в устройствах графического вывода. Но психофизиологическое восприятие света определяется не интенсивностью трех первичных цветов, а цветовым тоном, насыщенностью и светлотой. Цветовой тон позволяет различать цвета, насыщенность задает степень "разбавления" чистого тона белым цветом, а светлота - это интенсивность света в целом. Поэтому для адекватного нашему восприятию подбора оттенков более удобными являются модели, в числе параметров которых присутствует тон (Hue). Этот параметр принято измерять углом, отсчитываемым вокруг вертикальной оси. При этом красному цвету соответствует угол 0 , зеленому - 120 , синему - 240 , а дополняющие друг друга цвета расположены один напротив другого, т.е. угол между ними составляет 180 . Цвета CMY расположены посредине между составляющими их компонентами RGB. Существует две модели, использующие этот параметр.

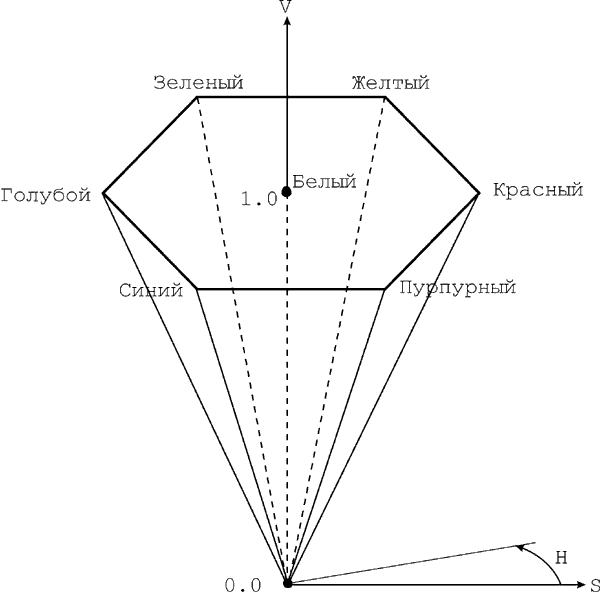
Модель HSV (Hue, Saturation, Value, или тон, насыщенность, количество света) можно представить в виде световой шестигранной пирамиды (рис. 2.10), по оси которой откладывается значение V, а расстояние от оси до боковой грани в горизонтальном сечении соответствует параметру S (за диапазон изменения этих величин принимается интервал от нуля до единицы). Значение S равно единице, если точка лежит на боковой грани пирамиды. Шестиугольник, лежащий в основании пирамиды, представляет собой проекцию цветового куба в направлении его главной диагонали (рис. 2.11).

Рис. 2.10. Цветовое пространство HSV

Рис. 2.11. Цветовое пространство HLS

Преобразование цветового пространства HSV в RGB осуществляется непосредственно с помощью геометрических соотношений между шестигранной пирамидой и кубом.

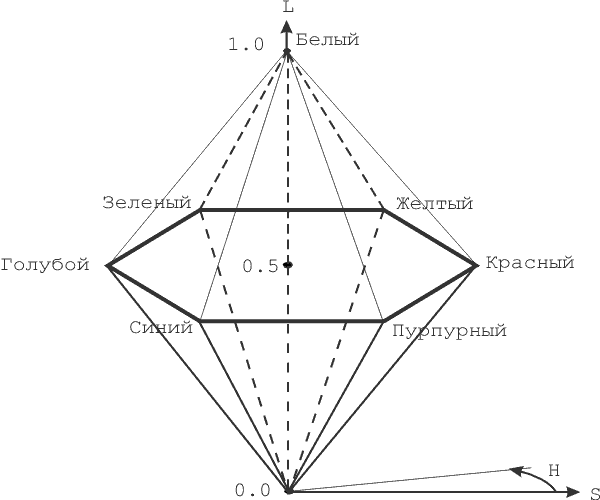
Цветовая модель HLS (Hue, Lightness, Saturation, или тон, светлота, насыщенность) является расширением модели HSV. Здесь цветовое пространство уже представляется в виде двойной пирамиды (рис. 2.11), в которой по вертикальной оси откладывается L (светлота), а остальные два параметра задаются так же, как и в предыдущей модели. В литературе эти пирамиды иногда называют шестигранным конусом.

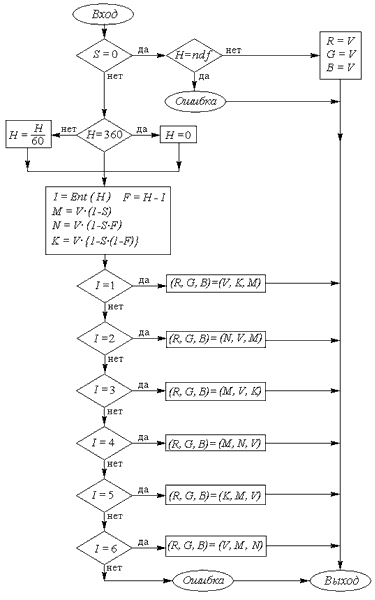
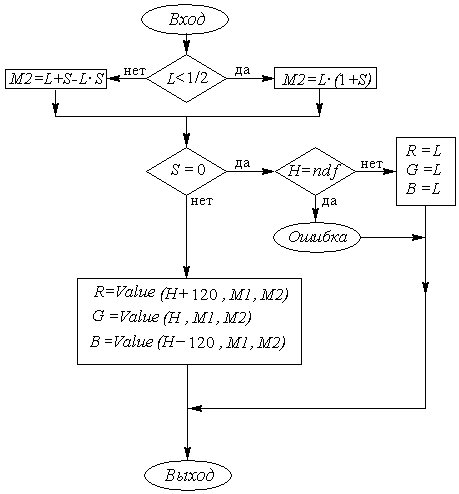
На рис. 2.12 и 2.13 приведены блок-схемы преобразования моделей HSV и HLS в модель RGB. Алгоритмы обратного преобразования предлагаются читателю в качестве упражнения.

В первом алгоритме используется функция Ent, означающая целую часть числа. Кроме того, используется операция присваивания для векторов. Константа ndf (сокращенное от выражения "not defined") используется при входе в алгоритм для того, чтобы выяснить, задано ли значение переменной H. Например, по соглашению ndf может быть некоторым отрицательным значением, так как тон - это всегда положительная величина. Во втором алгоритме применяется вспомогательная функция Value (H, M1, M2) для вычисления значения компоненты R, G или B в зависимости от ситуации.

увеличить изображение
Рис. 2.12. Преобразование модели HSV в RGB

Алгоритм преобразования:

Приведение H к заданному диапазону:
   Пока H<0 H=H+360
   Пока H>360 H=H-360
Определение координат
   Если H<60 то Value=M1+(M2-M1)*H/60
   Если 60<=H<180 то Value=M2
   Если 180<=H<240 то Value=M1+(M2-M1)*(240-H)/60
   Если 240<=H то Value=M1

Рис. 2.13. Преобразование модели HLS в RGB