Функциональные узлы комбинаторной логики. Дешифраторы
При синтезе логических выражений (4.2) учтено правило де Моргана для логических функций [2].
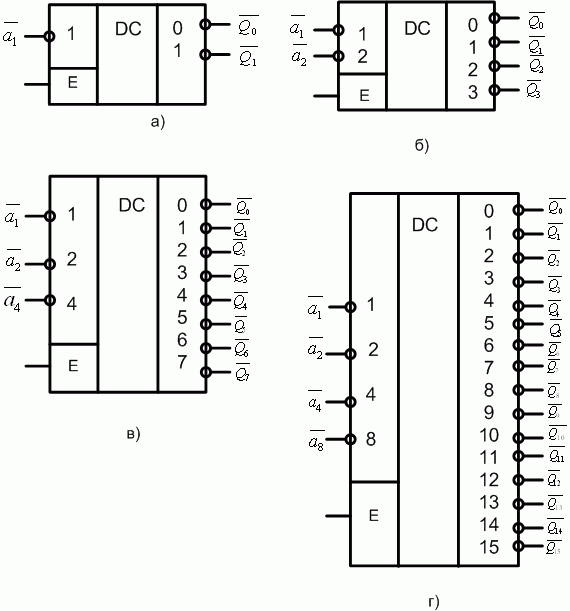
Рис. 4.4. УГО дешифраторов с активными нулевыми входами и выходами: а - на один вход; б - на два входа; в - на 3 входа; г - на 4 входа.
увеличить изображение
Рис. 4.5. Получение логических выражений для выходов дешифратора на три входа с инверсными входами и выходами.
Кроме представленных примеров, когда и входные и выходные сигналы имеют одинаковый активный уровень, возможен также синтез схем дешифраторов с разными активными уровнями входных и выходных сигналов. Рассмотрим случай, когда входные сигналы имеют активный единичный уровень, а выходные - нулевой. Таблица истинности такого дешифратора опять же на три входа приведена в табл. 4.3. Отличие от табл. 4.1 состоит в том, что состояние каждого выхода инверсно. Поэтому функциональная схема может быть реализована аналогично показанной на рис. 4.2, но вместо элементов И необходимо подключить элементы И-НЕ (рис. 4.6). Либо поскольку в каждом столбце таблицы истинности (табл. 4.3) имеется только один 0, логические выражения для выходов рационально представить в виде КНФ. Функциональная схема в этом случае будет иметь вид, показанный на рис. 4.7. Поскольку подача Е=1 переведёт в этой схеме все выходы дешифратора в неактивное единичное состояние, необходимо предусмотреть инвертор (рис. 4.7). При поступлении запрещающего сигнала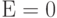 
приведёт к подаче логической 1 на все выходные элементы ИЛИ. Независимо от состояния входов 
, 
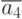и 
на всех выходах будут логические единицы, т.е. дешифратор не формирует унарный код.
Сравнение логических выражений для выходов дешифратора на рис. 4.6 и 4.7 очень наглядно иллюстрирует правило де Моргана - инверсия произведения сигналов эквивалентна сумме обратных сигналов [2]. УГО не зависит от функциональной схемы, оно отображает лишь активный уровень сигналов (рис. 4.4,в).
| Входные сигналы | Выходные сигналы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
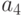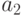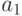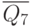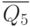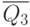| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
увеличить изображение
Рис. 4.6. Функциональная схема трех-входового дешифратора с единичным активным уровнем входных и нулевым - для выходных сигналов
увеличить изображение
Рис. 4.7. Функциональная схема трех-входового дешифратора с единичным активным уровнем входных и нулевым - для выходных сигналов
Разрешающий сигнал Е также может иметь активный уровень логического нуля. На рис. 4.8 показана функциональная схема, а на рис. 4.9 - УГО дешифратора на 2 входа с прямыми входами и выходами и инверсным разрешающим сигналом.
