НОУ ИНТУИТ | Основы цифровой техники. Лекция 3: Преобразователи произвольных кодов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 21.06.2011 | Доступ: свободный | Студентов: 2804 / 787 | Оценка: 4.02 / 4.11 | Длительность: 13:28:00

ISBN: 978-5-9556-0123-6

Теги: rs-триггер, алгебра, арифметика, задний фронт сигнала, инверсный выход, каскадная схема, КНФ, компоненты, логика, обратный код, оперативное запоминающее устройство, память, полевой транзистор, регистр адреса, регистровая память, шины, элементы

|

Вам нравится? Нравится 46 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматривается принцип синтеза логических схем, реализующих заданную математическую формулу.

Ключевые слова: логическая схема, алгоритм, метод минимизации

Преобразователь произвольных кодов - это логическая схема, реализующая определённую математическую формулу. На вход такой схемы подаётся двоичный код, соответствующий значению переменной 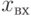$x_{вх}$ . На выходе схемы получается двоичный код, соответствующий значению функции $x_{вых}$ , вычисленному по указанной математической формуле.

В качестве примера синтеза логической схемы рассмотрим 3-входовую схему [2], реализующую увеличение входного кода в три раза: $x_{вых}=3x_{вх}$ . Последовательность действий при решении подобных задач следующая [3].

Определим максимально возможный код на выходе 3-входовой схемы: $7_{10} \times 3_{10} =21_{10}= 10101_{2}$ - это пятиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно пяти.
Заполним таблицу истинности для синтезируемой схемы (табл. 3.1). Поскольку количество выходов данной схемы больше одного, таблица включает в себя несколько (здесь пять ) столбцов, соответствующих двоичным разрядам выходного сигнала.
Для каждого выхода найдем минимальное выражение с помощью карт Карно (рис. 3.1).
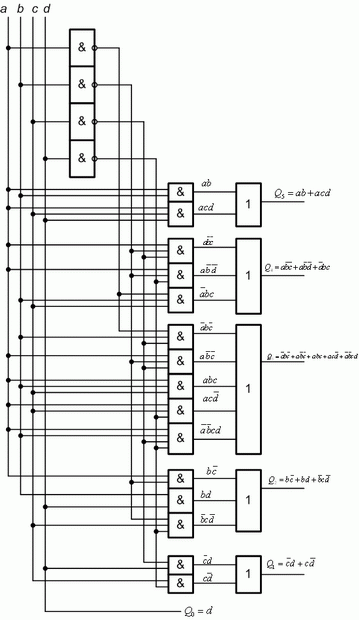
По полученным выражениям построим логическую схему на пять выходов, каждый из которых соответствует двоичному разряду вычисляемого по заданной формуле числа (рис. 3.2).

Таблица 3.1. Таблица истинности трех-входовой схемы умножения на 3
Входной код				Выходной код
В десятичном выражении	В двоичном коде			В десятичном выражении	В двоичном коде
					$Q_{4}$	$Q_{3}$	$Q_{2}$	$Q_{1}$	$Q_{0}$
	$2^{2}$	$2^{1}$	$2^{0}$		$2^{4}$	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$
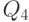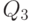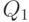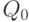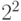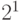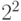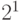0	0	0	0	0	0	0	0	0	0
1	0	0	1	3	0	0	0	1	1
2	0	1	0	6	0	0	1	1	0
3	0	1	1	9	0	1	0	0	1
4	1	0	0	12	0	1	1	0	0
5	1	0	1	15	0	1	1	1	1
6	1	1	0	18	1	0	0	1	0
7	1	1	1	21	1	0	1	0	1

$Минимизация логических выражений для выходных сигналов преобразователя, реализующего формулу x_{вых}=3x_{вх}$

увеличить изображение
Рис. 3.1. Минимизация логических выражений для выходных сигналов преобразователя, реализующего формулу x_{вых}=3x_{вх}

увеличить изображение
Рис. 3.2. Логическая схема преобразователя на 3 входа, реализующего формулу умножения на 3

Рассмотрим далее схему на 4 входа, реализующую ту же самую формулу $x_{вых}=3x_{вх}$ . Алгоритм решения тот же.

Определим максимально возможный код на выходе 4-входовой схемы: $15_{10} \times 3_{10} =45_{10}= 101101_{2}$ - это шестиразрядное двоичное число. Поэтому количество выходов для данной схемы будет равно шести.
Заполним таблицу истинности для синтезируемой схемы (табл. 3.2). Она включает в себя шесть столбцов, соответствующих двоичным разрядам выходного сигнала.
Для каждого выхода найдем минимальное выражение с помощью карт Карно (рис. 3.3).
По полученным выражениям построим логическую схему на шесть выходов, каждый из которых соответствует двоичному разряду вычисляемого по заданной формуле числа (рис. 3.4).
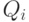Если весь столбец значений для выхода $Q_{i}=1$ , это означает, что независимо от состояния входных сигналов на выход $Q_{i}$ подаётся напряжение источника питания.
Если весь столбец значений для выхода 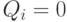$Q_{i}=0$ , это означает, что независимо от состояния входных сигналов выход 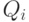$Q_{i}$ подключен к общей точке ("земле").

Таблица 3.2. Таблица истинности четырёх-входовой схемы умножения на 3
Входной код					Выходной код
В десятичном выражении	В двоичном коде				В десятичном выражении	В двоичном коде
						$Q_{5}$	$Q_{4}$	$Q_{3}$	$Q_{2}$	$Q_{1}$	$Q_{0}$
	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$		$2^{5}$	$2^{4}$	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$
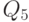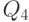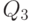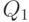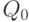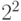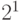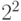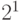0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	1	3	0	0	0	0	1	1
2	0	0	1	0	6	0	0	0	1	1	0
3	0	0	1	1	9	0	0	1	0	0	1
4	0	1	0	0	12	0	0	1	1	0	0
5	0	1	0	1	15	0	0	1	1	1	1
6	0	1	1	0	18	0	1	0	0	1	0
7	0	1	1	1	21	0	1	0	1	0	1
8	1	0	0	0	24	0	1	1	0	0	0
9	1	0	0	1	27	0	1	1	0	1	1
10	1	0	1	0	30	0	1	1	1	1	0
11	1	0	1	1	33	1	0	0	0	0	1
12	1	1	0	0	36	1	0	0	1	0	0
13	1	1	0	1	39	1	0	0	1	1	1
14	1	1	1	0	42	1	0	1	0	1	0
15	1	1	1	1	45	1	0	1	1	0	1

$Минимизация логических выражений для выходных сигналов 4-входового преобразователя, реализующего формулу x_{вых}=3x_{вх}$

увеличить изображение
Рис. 3.3. Минимизация логических выражений для выходных сигналов 4-входового преобразователя, реализующего формулу x_{вых}=3x_{вх}

увеличить изображение
Рис. 3.4. Логическая схема преобразователя на 4 входа, реализующего формулу умножения на 3

Дальше >>

Авторизоваться

Основы цифровой техники

Преобразователи произвольных кодов

Вопросы и ответы