НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 14: Прикладная теория организации очередей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Доступ: свободный | Студентов: 1059 / 208 | Оценка: 4.36 / 4.36 | Длительность: 22:21:00

Тема: Сетевые технологии

Специальности: Администратор коммуникационных систем, Архитектор программного обеспечения

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Основные результаты в теории организации очередей

Как упомянуто ранее, есть много различных моделей организации очереди но, к сожалению, есть только немного общих результатов в теории организации очереди. Литература по этому вопросу обширна, потому что много частных случаев, которые важны для практики. В этой секции мы рассмотрим самые важные общие результаты.

Формула Литтла, представленная в секции 5.3 - наиболее общий результат, который является справедливым для произвольной системы организации очереди. Теорема проста в применении и во многих случаях очень полезна.

В общем случае только системы организации очереди с Пуассонов-скими потоками вызовов просты для исследования. Относительно систем организации очереди при последовательном установлении соединения и организации очередей на сетях связи (например, компьютерных сетей) важно знать те случаи, где процесс выхода из системы организации очереди - Пуассоновский процесс. Эти системы организации очереди названы симметричными системами организации очереди, потому что они симметричны во времени, поскольку процесс поступления вызовов и процесс выхода из системы имеют один и тот же тип. Если для такой очереди рассматривать диаграмму процесса по тактам времени, невозможно решить, выполнена ли эта диаграмма при прямом или обратном процессе (обратимость). (Kelly, 1979 [60] ).

Классическая модель организации очереди играет ключевую роль в теории организации очереди, потому что другие системы будут часто сходиться к этой модели, когда число обслуживающих приборов будет увеличиваться (теорема Пальма 6.1 в секции 6.4).

Системы, которые больше всего отклоняются от классических моделей, являются системами с одним обслуживающим прибором. Однако они же являются самыми простыми для исследования.

В системах, работающих со временем ожидания, мы должны различать математическое ожидание вызова и математическое среднее время ожидания. Виртуальное время ожидания - это время ожидания, где вызов поступает в случайный момент времени (математическое ожидание времени). Фактическое время ожидания - это время ожидания реального вызова клиента (математическое ожидание вызова). Если процесс поступления вызовов - Пуассоновский процесс, то эти два математических ожидания идентичны.

Формула Полячека-Хинчина для M/G/1

Мы ранее получили среднее время ожидания для системы 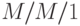M/M/1 (секция 12.2.4), и позже рассматривали 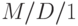M/D/1 (секция 13.5). В общем случае среднее время ожидания для 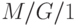M/G/1 определяется следующей теоремой.

Теорема 13.1 Формула Полячека-Хинчина (1930 -32):

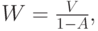$W=\frac{V}{1-A},$

( 13.1)

$W=\frac{A*s}{2(1-A)}* \varepsilon,$

( 13.2)

$V=A\frac s2 \varepsilon=\frac{\lambda}{2} m_2.$

( 13.3)

Здесь - среднее время ожидания обслуживания для всех клиентов, - среднее время обслуживания, - предложенная нагрузка, и е является коэффициентом формы распределения времени пребывания в системе (3.10).

Чем регулярнее процесс обслуживания, тем меньше среднее время ожидания. Соответствующий результат для процесса поступления вызовов изучен в секции 13.6. В реальной телефонной нагрузке коэффициент формы чаще всего равен 4-6, в нагрузке передачи данных 10-100.

Формула (13.2) - один из самых важных результатов в теории организации очереди, и мы изучим ее более тщательно.

Вывод формулы Полячека-Хинчина

Мы рассматриваем систему организации очереди M/G/1 и хотим найти среднее время ожидания обслуживания для произвольного клиента. Оно не зависит от дисциплины организации очереди, и поэтому можно далее принять, что это дисциплина FCFS. Из-за Пуассоновского потока вызовов ( свойство PASTA ) фактическое время ожидания клиентов равно виртуальному времени ожидания. Среднее время ожидания для произвольного клиента может быть разбито на две части.

Среднее время обслуживания от момента, когда клиент принимается на обслуживание, до момента окончания обслуживания. Поскольку мы рассматриваем случай, когда новый вызов поступает в случайный момент времени, остаточное среднее время обслуживания, данное (3.25):

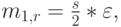
$m_{1,r}=\frac s2*\varepsilon,$
где и $\varepsilon$ имеют то же самое значение, как и в (13.2). Если процесс поступления вызовов - Пуассоновский процесс, вероятность поступления нового вызова в момент обслуживания другого клиента равна , потому что для системы с одним обслуживающим прибором мы всегда имеем 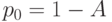(предложенная нагрузка равна обслуженной нагрузке).

Вклад в среднее время ожидания обслуживаемого клиента равен:

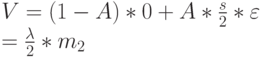
$V=(1-A)*0+A* \frac s2* \varepsilon\\ =\frac{\lambda}{2}*m_2$ ( 13.4)
.
Время ожидания из-за клиентов, ожидающих в очереди ( FCFS ). В среднем длина очереди - и определяется по теореме Литла:

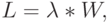
$L= \lambda*W,$
где - среднее число клиентов в очереди в произвольный момент времени, $\lambda$ является интенсивностью поступления вызовов, и - среднее время ожидания, которое мы ищем.

Для каждого клиента в очереди математическое ожидание времени обслуживания - единиц времени. Тогда среднее время ожидания из-за клиентов, стоящих в очереди, равно:

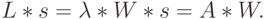$L*s=\lambda *W*s=A*W.$

( 13.5)

Таким образом, полное время ожидания равно (13.4) и (13.5):

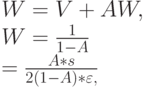
$W = V+AW, \\ W=\frac{1}{1-A}\\ =\frac{A*s}{2(1-A)* \varepsilon,$

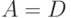и это отношение является Формулой Полячека-Хинчина (13.2). - среднее время ожидания для всех клиентов, тогда как среднее время ожидания для задержанных клиентов w становится ( A=D = вероятности задержки)(3.20):

$w=\frac WD=\frac{s}{2(1-A)}* \varepsilon.$

( 13.6)

Вышеупомянутый вывод справедлив, так как математическое ожидание по времени равно математическому ожиданию по вызовам, когда процесс поступления вызовов - Пуассоновский процесс ( свойство PASTA ).

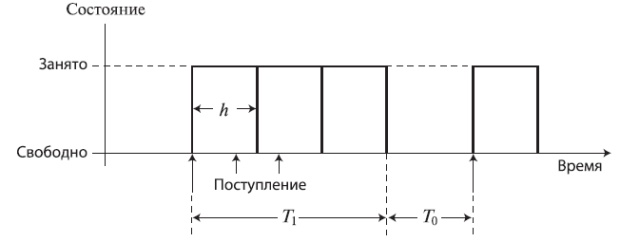
Период занятости для M/G/1

Период занятости системы организации очереди - временной интервал с момента, когда заняты все обслуживающие приборы, до момента, пока хотя бы один прибор не становится снова свободным. Для 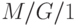M/G/1 средняя величина периода занятости вычисляется просто.

В какой-то момент система очередь становится пустой, она не имеет памяти из-за Пуассоновского потока вызовов. Эти моменты - точки регенерации очереди (точки равновесия), и следующее событие возникает согласно Пуассоновскому процессу с интенсивностью $\lambda$ .

Поэтому мы должны только рассматривать только цикл с момента изменения состояния обслуживающего прибора из свободного в занятое до следующего раза, когда она изменяет состояние из свободного в занятое. Этот цикл включает период занятости продолжительностью 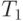T_1 и свободный период продолжительностью 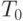T_0 . Pис.13.1 показывает пример с постоянным временем обслуживания.

Рис. 13.1.

Соотношение времени, когда система является занятой, тогда равно:

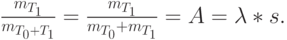$\frac{m_{T_1}}{m_{T_0+T_1}}=\frac{m_{T_1}}{m_{T_0}+m_{T_1}}=A=\lambda *s.$

( 13.7)

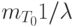Из $m_{T_0} 1/ \lambda$ мы имеем:

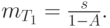
$m_{T_1}=\frac{s}{1-A}.$

В течение периода занятости обслуживается, по крайней мере, один клиент.

Время ожидания для M/G/1

Если рассматривать только клиентов, которые задержаны, можно найти моменты распределения времени ожидания для классических дисциплин организации очереди (Abate & Whitt, 1997 [1] ).

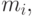FCFS. Обозначая как -тый момент распределения времени обслуживания m_i, мы можем найти k -тый момент распределения времени ожидания с помощью следующей рекурсивной формулы, где среднее время обслуживания выбрано как единица времени ( m_1 = s = 1 ):

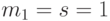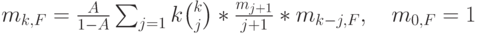$m_{k,F}=\frac{A}{1-A} \sum_{j=1}{k} {k\choose j}*\frac{m_{j+1}}{j+1}*m_{k-j,F}, \quad m_{0,F}=1$

( 13.8)

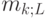LCFS. Из полученного выше момента $m_{k;F}$ распределения времени ожидания для FCFS мы можем найти момент $m_{k;L}$ для распределения времени ожидания LCFS. Три первых момента равны:

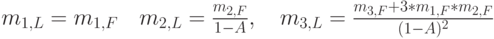$m_{1,L}=m_{1,F} \quad m_{2,L}=\frac{m_{2,F}}{1-A}, \quad m_{3,L}=\frac{m_{3,F}+3*m_{1,F}*m_{2,F}}{(1-A)^2}$

( 13.9)

Ограниченная длина очереди: M/G/1/k

В реальных системах длина очереди, например размер буфера, всегда будет конечна. Прием заявок, когда буфер полон, блокирован. Например, в Интернет эта стратегия применяется в маршрутизаторах и названа стратегией " отбрасывание хвоста ". При такой стратегии существует простое отношение между вероятностями состояний 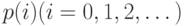$p(i) (i = 0, 1, 2, \dots)$ для бесконечной системы 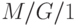M/G/1 и вероятностью состояний 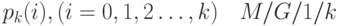$p_k (i), ( i = 0, 1, 2 \dots, k) \quad M/G/1/k$ для системы, в которой общее количество мест ожидания для клиентов конечно и равно , включая обслуживаемого клиента (Keilson, 1966 [59] ):

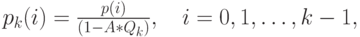$p_k(i)=\frac{p(i)}{(1-A*Q_k)}, \quad i=0,1, \dots, k-1,$

( 13.10)

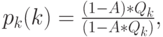$p_k(k)=\frac{(1-A)*Q_k}{(1-A*Q_k)},$

( 13.11)

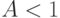где A < 1 - предложенная нагрузка

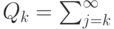$Q_k=\sum_{j=k}^{\infty}$

( 13.12)

Для такой стратегии существует алгоритм вычисления 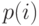p (i) при произвольном распределении времени пребывания в системе ( 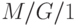M/G/1 ), основанный на анализе марковской вложенной цепи (Kendall,1953 [62] ), где тот же самый подход используется для ( GI/M/1 ).

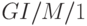Заметим, что это справедливо только для 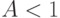A< 1 , но для конечного буфера мы также получаем статистическое равновесие при 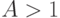A>1 . В этом случае нельзя применять подход, описанный в этой секции. Для 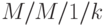M/M/1/k мы можем использовать конечную диаграмму переходов состояний, и для 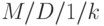M/D/1/k мы обсуждаем простой подход в секции 13.5.8, который применим для общих распределений времени пребывания в системе.

Приоритетные системы организации очередей: M/G/1

Существование времени ожидания обычно создает неудобства клиенту или лишние расходы. В соответствии с различными стратегиями организации очереди времена ожидания могут быть распределены среди клиентов согласно нашему предпочтению.

Комбинация нескольких классов клиентов

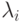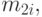В этом случае клиенты разделены на классов (потоков нагрузки). Предположим, что клиент класса создает Пуассоновский поток с интенсивностью $\lambda_i$ [в единицу времени] и среднее время обслуживания - s_i [единица времени]. Второй момент распределения времени обслуживания обозначим $m_{2i},$ предложенная нагрузка будет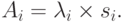 $A_i =\lambda_i \times s_i.$

Вместо того чтобы рассматривать отдельные процессы поступления вызовов, мы можем рассмотреть полный процесс поступления вызовов, который также является Пуассоновским потоком вызовов с интенсивностью:

$\lambda =\sum_{i=1}^N \lambda_i$

( 13.13)

В результате распределение времени обслуживания тогда становится взвешенной суммой распределений времени обслуживания отдельных классов (секция 3.2.2 - комбинация параллельных процессов). Полное среднее время обслуживания равно:

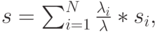$s=\sum_{i=1}^N \frac{\lambda_i}{\lambda}*s_i,$

( 13.14)

и полный второй момент:

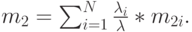$m_2=\sum_{i=1}^N \frac{\lambda_i}{\lambda}*m_{2i}.$

( 13.15)

Полная предложенная нагрузка:

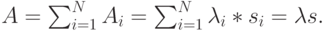$A=\sum_{i=1}^N A_i=\sum_{i=1}^N \lambda_i*s_i=\lambda s.$

( 13.16)

cреднее время ожидания обслуживания в случайный момент времени становится (13.4):

$V=\frac 12* \lambda*m_2$

( 13.17)

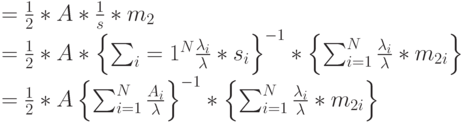
$=\frac 12*A*\frac 1s*m_2\\ =\frac 12*A* \left \{ \sum_i=1}^N \frac{\lambda_i}{\lambda}*s_i \right \}^{-1} * \left \{ \sum_{i=1}^N \frac{\lambda_i}{\lambda}*m_{2i} \right \}\\ =\frac 12*A \left \{\sum_{i=1}^N \frac{A_i}{\lambda} \right \}^{-1}* \left \{ \sum_{i=1}^N \frac{\lambda_i}{\lambda}*m_{2i} \right \}$

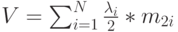$V=\sum_{i=1}^N \frac{\lambda_i}{2}*m_{2i}$

( 13.18)

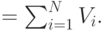$=\sum_{i=1}^N V_i.$

( 13.19)

Дальше >>

Авторизоваться

Разработка телетрафика и планирование сетей

Прикладная теория организации очередей