|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Прикладная теория организации очередей
Распределение времени ожидания: M/D/n, FCFS
Распределение времени ожидания определяется распределением Кроммелина:
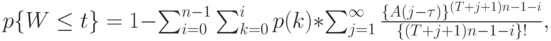 |
( 13.56) |
где  - предложенная нагрузка и:
- предложенная нагрузка и:
 |
( 13.57) |
В компактной форме по аналогии с (13.50):
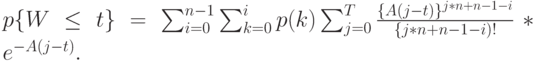 |
( 13.58) |
Для составных значений времени ожидания  мы имеем:
мы имеем:
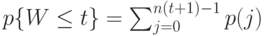 |
( 13.59) |
Для несоставных времен ожидания при  - целое число,
- целое число, 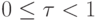 можно выразить распределение времени ожидания в элементах составных времен ожидания, поскольку для
можно выразить распределение времени ожидания в элементах составных времен ожидания, поскольку для 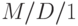 :
:
 |
( 13.60) |
где 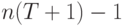 и
и 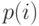 - вероятность состояния (13.55).
- вероятность состояния (13.55).
Точное среднее время ожидания всех клиентов получить  трудно. Приближенное значение получено Молина (Molina)
трудно. Приближенное значение получено Молина (Molina)
 |
( 13.61) |
Для любой системы с бесконечной очередью мы имеем (3.20):
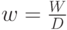
где:
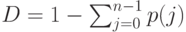
k -Эрланговский процесс поступления вызовов: Ek /D/r
Рассмотрим систему организации очереди к системе, в которой:  обслуживающих приборов (
обслуживающих приборов ( 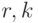 - целые числа), процесс поступления вызовов - общий, время обслуживания - постоянное и дисциплина организации очереди - FCFS. Клиенты, прибывающие в течение, когда обслуживающие приборы свободны, выбирают их в циклическом порядке:
- целые числа), процесс поступления вызовов - общий, время обслуживания - постоянное и дисциплина организации очереди - FCFS. Клиенты, прибывающие в течение, когда обслуживающие приборы свободны, выбирают их в циклическом порядке:
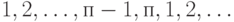
Тогда некоторый обслуживающий прибор обслужит только каждого  -ого клиента, так как клиенты из-за постоянного времени обслуживания освобождают обслуживающие приборы в том же порядке, в каком они занимают обслуживающие приборы. Ни один клиент не может догнать другого клиента в очереди.
-ого клиента, так как клиенты из-за постоянного времени обслуживания освобождают обслуживающие приборы в том же порядке, в каком они занимают обслуживающие приборы. Ни один клиент не может догнать другого клиента в очереди.
Пусть обслуживающие приборы разбиты на группы, тогда
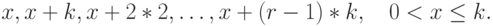 |
( 13.62) |
прибор в группе обслужит только каждого  -ого клиента. Если мы рассматриваем обслуживающие приборы в (13.62) как одну группу, то они эквивалентны системе организации очереди
-ого клиента. Если мы рассматриваем обслуживающие приборы в (13.62) как одну группу, то они эквивалентны системе организации очереди  , где процесс поступления вызовов
, где процесс поступления вызовов  есть свертка распределения времени прибытия отдельных
есть свертка распределения времени прибытия отдельных  времен.
времен.
То же самое относится к другим  системам. Нагрузка в этих
системам. Нагрузка в этих  системах является взаимно коррелированной, но если рассматривать только одну систему одновременно, то она -
системах является взаимно коррелированной, но если рассматривать только одну систему одновременно, то она -  , FCFS -система организации очереди.
, FCFS -система организации очереди.
Предположение о циклическом поиске обслуживающих приборов в пределах отдельных систем обязательно (13.62). Вероятности состояния, средние времена ожидания и т.д. не зависят от дисциплины организации очереди, которая играет важную роль только для распределения времени ожидания.
Если мы предположим, что GI -процесс поступления вызовов - Пуассоновский процесс, то  становится k-Эрланговским процессом поступления вызовов. Таким образом, мы получили, что следующие системы эквивалентны относительно распределения времени ожидания:
становится k-Эрланговским процессом поступления вызовов. Таким образом, мы получили, что следующие системы эквивалентны относительно распределения времени ожидания:

Поэтому система 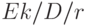 может работать с таблицами для
может работать с таблицами для 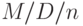 .
.
Вообще мы знаем, что нагрузка на один обслуживающий прибор и среднее времени ожидания уменьшается, когда число обслуживающих приборов увеличивается. По той же причине среднее время ожидания уменьшается, когда процесс поступления вызовов становится более регулярным. Это замечено непосредственно из вышеупомянутого разложения, где процесс поступления вызовов для 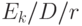 становится более регулярным при увеличении
становится более регулярным при увеличении  (
(  константа). Для = 0,9 Эрл. на один обслуживающий прибор (
константа). Для = 0,9 Эрл. на один обслуживающий прибор (  = средняя длина очереди) находим:
= средняя длина очереди) находим:

Система с конечной очередью: M/D/1/k
В реальных системах мы всегда имеем конечную очередь. В компьютерных системах размер памяти конечен, и в системах ATM существуют конечные буфера. То же самое происходит для мест ожидания в гибких производственных системах ( FMS - Flexible Manufacturing Systems ).
Как показано в секции 13.3.4, вероятности состояния  для конечной буферной системы получены из вероятностей состояний
для конечной буферной системы получены из вероятностей состояний 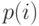 бесконечной буферной системы, используя (13.10) и (13.11).
бесконечной буферной системы, используя (13.10) и (13.11).
Составные времена ожидания получены из вероятностей состояний и несоставных времен ожидания - из составных времен ожидания, как показано выше (секция 13.5.4).
Для бесконечной буферной системы вероятности состояния существуют только, когда предложенная нагрузка меньше, чем емкость 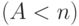 . Но для конечной буферной системы вероятности состояния существуют и для
. Но для конечной буферной системы вероятности состояния существуют и для 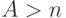 , однако мы не можем получить их вышеупомянутым методом.
, однако мы не можем получить их вышеупомянутым методом.
В 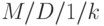 конечные буферные вероятности состояния
конечные буферные вероятности состояния  могут быть получены для любой предложенной нагрузки следующим способом.
могут быть получены для любой предложенной нагрузки следующим способом.
В системе с одним сервером и  местами ожидания мы имеем
местами ожидания мы имеем  состояний
состояний  . Уравнения равновесия для вероятностей состояния
. Уравнения равновесия для вероятностей состояния 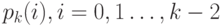 , составляя
, составляя  линейных уравнений между состоянием
линейных уравнений между состоянием 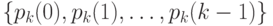 , могут быть установлены с помощью уравнений состояний Фрея. Но невозможно записать простые уравнения времени для состояния
, могут быть установлены с помощью уравнений состояний Фрея. Но невозможно записать простые уравнения времени для состояния  и
и  . Однако первые
. Однако первые  уравнения (13.41) вместе с требованием нормализации:
уравнения (13.41) вместе с требованием нормализации:
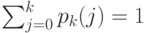 |
( 13.63) |
и фактом, что предложенная нагрузка равняется обслуженной нагрузке плюс отклоненная нагрузка ( свойство PASTA ) дают
 |
( 13.64) |
в результате 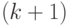 независимых линейных уравнений, которые легко решить.
независимых линейных уравнений, которые легко решить.
Два подхода дают, конечно, один и тот же результат. Первый метод справедлив только для  , тогда как второй - для любой предложенной нагрузки.
, тогда как второй - для любой предложенной нагрузки.
Пример 13.5.2: "Дырявое ведро"
"Дырявое ведро" - механизм для управления процессами поступления ячеек (пакетов) от пользователя (источника) в ATM -системе. Механизм соответствует системе организации очереди с постоянным временем обслуживания (размер ячейки) и конечным буфером. Если процесс поступления вызовов - Пуассоновский процесс, то мы имеем систему 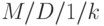 . Размер "вытекания" из дыры соответствует долгосрочной средней интенсивности поступления, тогда как размер "ведра" описывает допустимый избыток (число пакетов). Механизм работает как виртуальная система организации очереди, где ячейки или принимаются немедленно, или отклоняются согласно значению счетчика, который является составным значением функции нагрузки (рис.13.2). В контракте между пользователем и сетью соглашение заключается при заданном размере утечки и размере "ведра". На этом основании сеть способна гарантировать заданный уровень обслуживания.
. Размер "вытекания" из дыры соответствует долгосрочной средней интенсивности поступления, тогда как размер "ведра" описывает допустимый избыток (число пакетов). Механизм работает как виртуальная система организации очереди, где ячейки или принимаются немедленно, или отклоняются согласно значению счетчика, который является составным значением функции нагрузки (рис.13.2). В контракте между пользователем и сетью соглашение заключается при заданном размере утечки и размере "ведра". На этом основании сеть способна гарантировать заданный уровень обслуживания.
Система организации очереди с одним обслуживающим прибором: GI/G/1
В секции 13.3 мы показали, что среднее время ожидания для всех клиентов в системе организации очереди 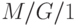 определяется формулой Полячека-Хинчина:
определяется формулой Полячека-Хинчина:
 |
( 13.65) |
где  - коэффициент формы распределения времени пребывания в системе.
- коэффициент формы распределения времени пребывания в системе.
Ранее мы анализировали следующие случаи.
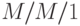 (секция 12.2.4):
(секция 12.2.4):  :
:
 |
( 13.66) |
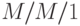 (секция 13.5.3):
(секция 13.5.3):  :
:
 |
( 13.67) |
Показано, что чем регулярнее распределение времени пребывания в системе, тем меньше становится нагрузка времени ожидания (для систем с потерями и с ограниченной доступностью этот эффект противоположен: чем больше коэффициент формы, тем меньше потери).
В системах с не пуассоновским поступлением моменты более высокого порядка будут также влиять на среднее время ожидания.
Общие результаты
Мы до настоящего времени принимали, что процесс поступления вызовов - Пуассоновский процесс. Для других процессов поступления вызовов редко можно найти точное выражение среднего времени ожидания, кроме случаев, где времена пребывания в системе дают основания предлагать, что или процесс поступления вызовов, или процесс обслуживания - марковские. До настоящего времени нет никаких общих точных формул, например, для 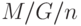 .
.
Для 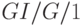 можно получить теоретические верхние пределы для среднего времени ожидания. Обозначая дисперсию интервалов поступления va и дисперсию распределения времени пребывания в системе -
можно получить теоретические верхние пределы для среднего времени ожидания. Обозначая дисперсию интервалов поступления va и дисперсию распределения времени пребывания в системе -  с помощью неравенства Кингмана (1961) мы получаем верхний предел для среднего времени ожидания:
с помощью неравенства Кингмана (1961) мы получаем верхний предел для среднего времени ожидания:
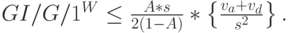 |
( 13.68) |
Эта формула показывает, что мы имеем дело со стохастическими вариациями времен ожидания.
Формула (13.68) дает теоретическую верхнюю границу. Реалистическая оценка фактического среднего времени ожидания получена приближением Марчала (Marchal, 1976)
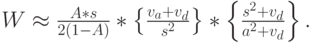 |
( 13.69) |
где  - средний интервал поступления (
- средний интервал поступления (  ). Это приближение получается масштабированием приближенного неравенства Кингмана, что согласуется с Формулой Полячека-Хинчина для случая
). Это приближение получается масштабированием приближенного неравенства Кингмана, что согласуется с Формулой Полячека-Хинчина для случая 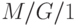 .
.
Как пример непуассоновского потока вызовов, мы проанализируем систему организации очереди 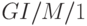 , где распределение интервалов поступления - общее распределение, данное плотностью распределения
, где распределение интервалов поступления - общее распределение, данное плотностью распределения  . Времена обслуживания являются экспоненциально распределенными со скоростью
. Времена обслуживания являются экспоненциально распределенными со скоростью 
Если систему рассматривают в произвольном момент времени, то вероятности состояния не будут отображаться марковским процессом, потому что вероятность прибытия будет зависеть от временного интервала, начиная с последнего прибытия, и свойство PASTA не будет выполняться.
Однако если систему рассматривать непосредственно до (или после) момента поступления, то она будет независима, так как интервалы поступления стохастическая независимы от времени пребывания в системе и являются экспоненциально распределенными. Моменты поступления - это точки равновесия (пункты регенерации, секция 5.2.2), и мы рассматриваем так называемую вложенную цепь Маркова.
Вероятность, что перед моментом поступления система находится в состоянии  , будем обозначать
, будем обозначать  . Можно показать, что при статистическом равновесии будет получен следующий результат D.G. Kendall, 1953 [62] :
. Можно показать, что при статистическом равновесии будет получен следующий результат D.G. Kendall, 1953 [62] :
 |
( 13.70) |
где  - положительный реальный корень, удовлетворяющий уравнению:
- положительный реальный корень, удовлетворяющий уравнению:
 |
( 13.71) |
Устойчивые вероятности состояния могут быть получены при рассмотрении двух последовательных моментов поступления 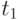 и
и 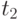 (подобно уравнениям состояния Фрея, секция 13.5.5).
(подобно уравнениям состояния Фрея, секция 13.5.5).
Так как процесс отклонения - Пуассоновский процесс с постоянной интенсивностью  , когда есть клиенты в системе, то вероятность
, когда есть клиенты в системе, то вероятность 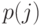 , что для
, что для  клиентов обслуживание будет закончено между двумя моментами поступления, может быть выражена числом событий в Пуассоновском процессе в течение стохастического интервала (интервал поступления). Существуют следующие уравнения состояний:
клиентов обслуживание будет закончено между двумя моментами поступления, может быть выражена числом событий в Пуассоновском процессе в течение стохастического интервала (интервал поступления). Существуют следующие уравнения состояний:
 |
( 13.72) |
Условие нормализации определяется обычно так:
 |
( 13.73) |
Можно показать, что для вышеупомянутого геометрического распределения это единственное решение данной системы уравнений (Kendall, 1953 [62] ).
В принципе, система организации очереди  может быть рассмотрена с помощью того же способа, что и предыдущая. Тогда вероятность состояния
может быть рассмотрена с помощью того же способа, что и предыдущая. Тогда вероятность состояния  становится более сложной, так как интенсивность освобождения зависит от числа занятых каналов.
становится более сложной, так как интенсивность освобождения зависит от числа занятых каналов.
Заметим, что  - не вероятность нахождения системы в состоянии
- не вероятность нахождения системы в состоянии  в произвольный момент времени (математическое ожидание по времени), а вероятность нахождения системы в состоянии
в произвольный момент времени (математическое ожидание по времени), а вероятность нахождения системы в состоянии  непосредственно перед прибытием (вызвать математическое ожидание вызова).
непосредственно перед прибытием (вызвать математическое ожидание вызова).
Характеристики GI/M/1
Вероятность непосредственного обслуживания становится:
 |
( 13.74) |
Соответствующая вероятность того, чтобы выполнение заявки было отсрочено, становится:
 |
( 13.75) |
Среднее число занятых обслуживающих приборов в случайный момент времени (математическое ожидание по времени) равно обслуженной нагрузке (= предложенная нагрузка 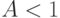 ).
).
Среднее число ждущих клиентов, непосредственно перед прибытием клиента, может быть получено с помощью вероятности состояний:
 |
( 13.76) |
Среднее число клиентов в системе перед моментом поступления вызова:
 |
( 13.77) |
Среднее время ожидания для всех клиентов тогда равно:
 |
( 13.78) |
Средняя длина очереди, по всей оси (виртуальная длина очереди) поэтому равна (формула Литтла):
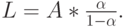 |
( 13.79) |
Среднее время ожидания для клиентов, которые стоят в очереди, равно:
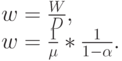 |
( 13.80) |
