|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Многомерные системы с потерями
Пример 10.3.1: Модель Роннблома (Rцnnblom's model)
Первый пример модели мультислотового трафика был опубликован Роннбломом (1958 [92]). Статья рассматривает внешнюю нагрузку (исходящую и входящую) и внутреннюю нагрузку в учрежденческой телефонной станции ( PABX ) с двусторонними каналами. Внешняя нагрузка занимает только один канал на вызов. Внутренняя нагрузка занимает и исходящий канал, и входящий канал и таким образом требует двух каналов одновременно. Роннблом показал, что эта модель имеет форму произведения.
Пример 10.3.2: Два потока нагрузки
Проиллюстрируем вышеупомянутые модели маленьким исследованием. Мы рассматриваем пучок из 6 каналов, на который поступают два потока нагрузки, указанные в таблице 10.1. Пусть второй поток нагрузки - поток мультислотового трафика. Пусть в нашей системе может быть не более трех вызовов типа 2.
Мы должны определить только предложенную нагрузку, не определяя абсолютные значения интенсивности поступления и скорости обслуживания. Предложенная нагрузка, как обычно, определяется как нагрузка, которую несет пучок из бесконечного числа каналов.
На рис.10.4 показана двухмерная диаграмма переходов состояний. Полная сумма всех вероятностей состояний равняется 20,1704. После нормализации мы находим  а также следующие вероятности состояния и безусловные вероятности состояний
а также следующие вероятности состояния и безусловные вероятности состояний 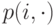 и
и 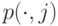 .
.

Рис. 10.4. Пример 10.3.2: на шесть каналов поступает два Пуассоновских потока нагрузки (PCT-I) (горизонтальные линии состояний) и энгсетовский поток нагрузки (PCT-II) (вертикальные линии состояний). Параметры определены в Таблице 10.1. Если мы определим условную вероятность состояния (0, 0) равной единице, тогда, используя локальное равновесие вероятностей состояний, мы сможем найти условное состояние q(i, j), показанное ниже
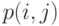 |
 |
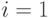 |
 |
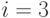 |
 |
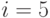 |
 |
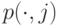 |
|---|---|---|---|---|---|---|---|---|
| j=6 | 0.0073 | 0.0073 | ||||||
| j=4 | 0.0331 | 0.0661 | 0.0661 | 0.1653 | ||||
| j=2 | 0.0661 | 0.1322 | 0.1322 | 0.0881 | 0.0441 | 0.4627 | ||
| j=0 | 0.0496 | 0.0992 | 0.0992 | 0.0661 | 0.0331 | 0.0132 | 0.0044 | 0.3647 |
 |
0.1561 | 0.2975 | 0.2975 | 0.1542 | 0.0771 | 0.0132 | 0.0044 | 1.0000 |
Глобальные вероятности состояния получаются:
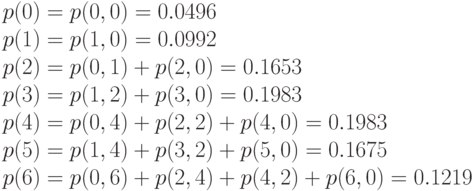
Критерии качества работы для потока 1
В соответствии со свойствами потока PASTA потери по времени (  ), потери по вызовам (
), потери по вызовам (  ) и по нагрузке (
) и по нагрузке (  ) - равны. Мы найдем потери по времени
) - равны. Мы найдем потери по времени  :
:

Критерии качества работы для потока 2
Потери по времени  (соотношение времени блокировки системы для потока 2):
(соотношение времени блокировки системы для потока 2):
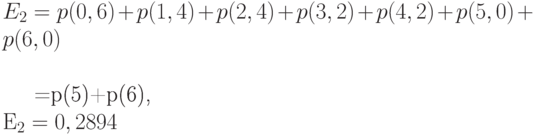
Потери по вызовам  (соотношение попыток вызова, блокированных для потока 2):
(соотношение попыток вызова, блокированных для потока 2):
Общее количество попыток вызова в единицу времени получено из безусловного (одномерного) распределения:
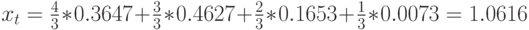
Число блокированных попыток вызова в единицу времени получается:

Следовательно,
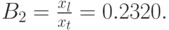
Потери по нагрузке 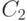 (соотношение блокированной и предложенной нагрузки):
(соотношение блокированной и предложенной нагрузки):
Обслуженная нагрузка, измеренная для канала, получена из безусловного (одномерного) распределения:
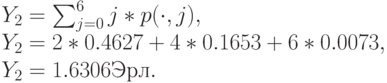
Предложенная нагрузка, измеренная на канал, равна 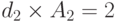 Эрл. (Таблица. 10.1). Следовательно, мы имеем:
Эрл. (Таблица. 10.1). Следовательно, мы имеем:

Рассмотренный выше пример имеет только 2 потока и 6 каналов, и общее количество состояний равняется 16 (рис.10.4). Когда число потоков нагрузки и каналов увеличивается, число состояний очень быстро увеличивается, и невозможно оценить систему, вычисляя отдельные вероятности состояния. В следующей секции мы вводим алгоритм свертки для систем с потерями, который устраняет эту проблему увеличения состояний.
Алгоритм свертки для систем с потерями
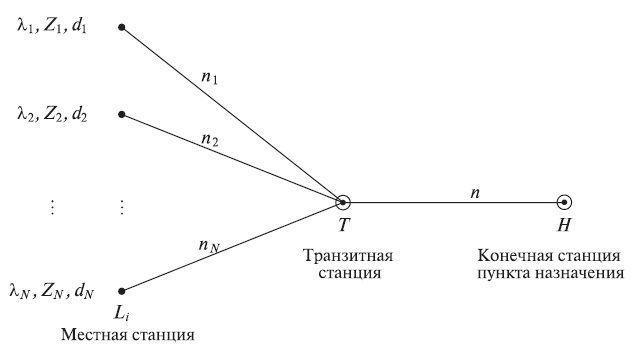
Теперь рассмотрим группу пучков каналов с общим количеством n гомогенных пучков каналов. Гомогенными мы в данном случае называем каналы, имеющие одну ту же скорость. На группу пучков каналов поступают N различных типов вызовов, называемых потоками, или классами. Вызов типа i требует  пучков каналов (каналы, слоты) в течение всего времени обслуживания, то есть занятия и освобождения одновременно всех каналов
пучков каналов (каналы, слоты) в течение всего времени обслуживания, то есть занятия и освобождения одновременно всех каналов  .
.
Процессы поступления вызовов - общие зависимые от состояния Пуассоновские процессы. Для i -того процесса поступления вызовов интенсивность прибытия в состоянии  то есть когда вызовы
то есть когда вызовы  типа i обслуживаются, интенсивность равна
типа i обслуживаются, интенсивность равна 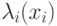 . Мы можем ограничить число xi одновременных вызовов типа i так, чтобы:
. Мы можем ограничить число xi одновременных вызовов типа i так, чтобы:

Будет естественно потребовать, чтобы 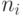 было составным числом, кратным
было составным числом, кратным  Эта модель описывает, например, систему, показанную на рис.10.5.
Эта модель описывает, например, систему, показанную на рис.10.5.
Обобщение классического телетрафика показывает нагрузку BPP и мультислотовый трафик. Параметры 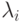 и
и  описывают нагрузку BPP, тогда как
описывают нагрузку BPP, тогда как  обозначает число требуемых слотов.
обозначает число требуемых слотов.
Упомянутая выше система может быть оценена эффективным способом - алгоритмом свертки, впервые введенным в (Iversen, 1987 [40]). Сначала опишем алгоритм, а затем объясним на примере дальнейшие детали. Алгоритм свертки близко связан с формой произведения.
Алгоритм
Алгоритм представлен следующими тремя шагами.
Шаг 1. Вычислите вероятности состояния каждого потока нагрузки, как будто он является единственным в системе, то есть мы рассматриваем классические системы с потерями, как это отображается в Лекциях 7 и 8. Для нагрузки потока i мы находим:
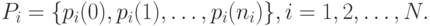 |
( 10.22) |
Важны только условные значения 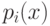 , так что мы можем выбрать
, так что мы можем выбрать  и вычислить значения
и вычислить значения 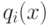 относительно
относительно  . Если элемент
. Если элемент 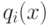 становится больше, чем K (например
становится больше, чем K (например 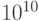 ), тогда мы можем разделить все значения
), тогда мы можем разделить все значения  , на K. Чтобы избежать любых проблем вычислений, в дальнейшем желательно нормировать условные вероятности состояний так, чтобы:
, на K. Чтобы избежать любых проблем вычислений, в дальнейшем желательно нормировать условные вероятности состояний так, чтобы:

Шаг 2. Последовательным свертыванием (оператор свертывания *) мы вычисляем совокупную вероятность состояния для полной системы за исключением потока нагрузки i:
 |
( 10.23) |
Сначала свертываем  и
и  и получаем
и получаем  который свертывается с
который свертывается с  и т.д. Оба закона - коммутативный и ассоциативный - справедливы для оператора свертывания и определены обычным способом (секция 3.2):
и т.д. Оба закона - коммутативный и ассоциативный - справедливы для оператора свертывания и определены обычным способом (секция 3.2):
 |
( 10.24) |
где
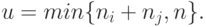 |
( 10.25) |
Заметьте, что производится усечение пространства состояний к  состояниям. Даже если
состояниям. Даже если  и
и 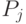 нормированы, результат свертки в общем случае не нормирован из-за усечения. Его рекомендуется нормировать после каждого свертывания, чтобы избежать любых проблем при вычислении в течение этого шага и на следующем.
нормированы, результат свертки в общем случае не нормирован из-за усечения. Его рекомендуется нормировать после каждого свертывания, чтобы избежать любых проблем при вычислении в течение этого шага и на следующем.
Шаг 3. Вычислите потери по времени 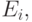 потери по вызовам
потери по вызовам  и потери по нагрузке
и потери по нагрузке 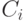 потока
потока  . Это может быть сделано в процессе свертки:
. Это может быть сделано в процессе свертки:

Свертка заканчивается:
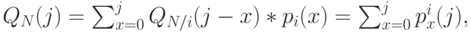 |
( 10.26) |
где для  обозначает поток нагрузки,
обозначает поток нагрузки,  - общее количество занятых каналов и
- общее количество занятых каналов и  - число каналов, занятых потоком
- число каналов, занятых потоком  . Шаги 2-3 повторяются для каждого потока нагрузки.
. Шаги 2-3 повторяются для каждого потока нагрузки.
Далее мы получаем формулы для  и
и 
Потери по времени 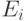 для нагрузки потока i получаются:
для нагрузки потока i получаются:
 |
( 10.27) |
где
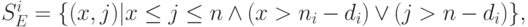
Суммирование по всем  расширенным состояниям, где вызовы, принадлежащие классу
расширенным состояниям, где вызовы, принадлежащие классу  , блокированы: набор
, блокированы: набор  соответствует состоянию, в котором поток нагрузки,
соответствует состоянию, в котором поток нагрузки,  использовал свою квоту, и соответственно число состояний с меньше чем
использовал свою квоту, и соответственно число состояний с меньше чем  свободных каналов.
свободных каналов.  - нормировочная константа:
- нормировочная константа:
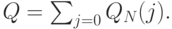
(На этом этапе мы обычно нормируем вероятности состояния так, чтобы 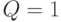 )
)
 потери по вызовам для нагрузки потока
потери по вызовам для нагрузки потока  - это отношение числа блокированных попыток вызова к общему числу попыток вызовов (оба числа берутся для потока нагрузки
- это отношение числа блокированных попыток вызова к общему числу попыток вызовов (оба числа берутся для потока нагрузки  в единицу времени). Мы находим:
в единицу времени). Мы находим:
 |
( 10.28) |
Потери по нагрузке  Мы определяем их, как обычно предложенную нагрузку, которую обслуживает бесконечная группа пучков каналов. Обслуженная нагрузка для нагрузки потока
Мы определяем их, как обычно предложенную нагрузку, которую обслуживает бесконечная группа пучков каналов. Обслуженная нагрузка для нагрузки потока  :
:
 |
( 10.29) |
Таким образом, мы находим:

Алгоритм реализован в программном обеспечении ATMOS (Листов, Сааби, Иверсен (Listov, Saabye и Iversen, 1989 [74]). Требование к памяти (накопителю) пропорционально  . Она используется для вычисления вероятности состояния потока нагрузки, когда это необходимо. Практически мы используем память, пропорциональную
. Она используется для вычисления вероятности состояния потока нагрузки, когда это необходимо. Практически мы используем память, пропорциональную  , потому что сохраняем промежуточные результаты свертывания для более позднего повторного использования. Можно показать (Иверсен и Степанов, 1997 [42]), что нам необходимо (
, потому что сохраняем промежуточные результаты свертывания для более позднего повторного использования. Можно показать (Иверсен и Степанов, 1997 [42]), что нам необходимо (  ) свертывания, когда мы вычисляем характеристики нагрузки для всех
) свертывания, когда мы вычисляем характеристики нагрузки для всех  потоков нагрузки. Таким образом, время вычисления подчиняется линейной зависимости от
потоков нагрузки. Таким образом, время вычисления подчиняется линейной зависимости от  и квадратичной для
и квадратичной для  .
.
Пример 10.4.1: развертка
В принципе мы можем получить  из
из  разверткой и затем в течение повторной свертки
разверткой и затем в течение повторной свертки  вычислить критерии качества работы. При этом способе мы не должны повторять все свертки (10.23) для каждого потока нагрузки. Но при осуществлении этого подхода имеются проблемы вычислений. Свертка, с точки зрения вычисления, очень устойчива, а развертка вычисляется не всегда. Однако мы можем применить развертку в некоторых случаях, например, когда источники нагрузки имеют два состояния - вкл\выкл.
вычислить критерии качества работы. При этом способе мы не должны повторять все свертки (10.23) для каждого потока нагрузки. Но при осуществлении этого подхода имеются проблемы вычислений. Свертка, с точки зрения вычисления, очень устойчива, а развертка вычисляется не всегда. Однако мы можем применить развертку в некоторых случаях, например, когда источники нагрузки имеют два состояния - вкл\выкл.
Пример 10.4.2: Три потока нагрузки
Мы сначала проиллюстрируем алгоритм небольшим примером, где детально покажем вычисления. Рассмотрим систему с 6 каналами и 3 потоками нагрузки. В дополнение к двум потокам в Примере 10.3.2 складываем поток Паскаля с ограничением класса, как показано в Таблице 10.2 (см. Пример 8.7.2). Мы хотим вычислить критерии качества работы потока нагрузки 3.
Шаг 1. Вычисляем 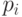 вероятностей состояния
вероятностей состояния  каждого потока нагрузки
каждого потока нагрузки  , как будто он существут один. Результаты даются в Таблице 10.3.
, как будто он существут один. Результаты даются в Таблице 10.3.
Шаг 2. Оцениваем свертывание  , усекаем пространство состояний до
, усекаем пространство состояний до  , нормализуем вероятности так, чтобы мы получить
, нормализуем вероятности так, чтобы мы получить 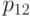 , показанное в Таблице 10.3. Заметим, что это - результат, полученный в Примере 10.3.2.
, показанное в Таблице 10.3. Заметим, что это - результат, полученный в Примере 10.3.2.
Шаг 3. Свертываем  , усекаем в
, усекаем в  и получаем
и получаем 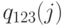 , как показано в Таблице 10.3. Потери по времени
, как показано в Таблице 10.3. Потери по времени 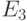 получены из детальных вероятностей состояния.
получены из детальных вероятностей состояния.
В потоке нагрузки 3 (единственный слот) потери по времени возникают, по опыту, в двух случаях: либо когда все шесть каналов заняты, либо когда поток нагрузки занимает 4 канала (максимальное распределение). Из детальных вероятностей состояния мы получаем:

| Состояние | Вероятности |  |
Нормализованная | Вероятности | 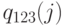 |
Нормализованная | |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| 0 | 0.1360 | 0.3176 | 0.0432 | 0.0496 | 0.4525 | 0.0224 | 0.0259 |
| 1 | 0.2719 | 0.0000 | 0.0864 | 0.0992 | 0.3017 | 0.0599 | 0.0689 |
| 2 | 0.2719 | 0.4235 | 0.1440 | 0.1653 | 0.1508 | 0.1122 | 0.1293 |
| 3 | 0.1813 | 0.0000 | 0.1727 | 0.1983 | 0.0670 | 0.1579 | 0.1819 |
| 4 | 0.0906 | 0.2118 | 0.1727 | 0.1983 | 0.0279 | 0.1825 | 0.2104 |
| 5 | 0.0363 | 0.0000 | 0.1459 | 0.1675 | 0.0000 | 0.1794 | 0.2067 |
| 6 | 0.0121 | 0.0471 | 0.1062 | 0.1219 | 0.0000 | 0.1535 | 0.1769 |
| Всего | 1.0000 | 1.0000 | 0.8711 | 1.0000 | 1.0000 | 0.8678 | 1.0000 |
Заметим, что состояния  , включены в состояние
, включены в состояние  . Обслуженная нагрузка для потока нагрузки 3 получена в процессе свертывания
. Обслуженная нагрузка для потока нагрузки 3 получена в процессе свертывания  и
и  и равна:
и равна:
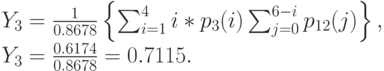
Потери по нагрузке:
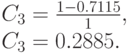
Потери по вызовам равны:

где 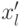 является числом вызовов, потерянных в единицу времени, и
является числом вызовов, потерянных в единицу времени, и 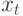 - общее количество попыток вызова в единицу времени. Используя нормализованные вероятности, из Таблицы 10.3 мы получаем:
- общее количество попыток вызова в единицу времени. Используя нормализованные вероятности, из Таблицы 10.3 мы получаем:

Тем же способом, обмениваясь результатом свертки нагрузки потока, находим критерии качества работы потока 1 и 2. Общее количество микросостояний в этом примере - 47. Методом свертки уменьшаем число состояния так, чтобы нам никогда не понадобилось более, чем два вектора по  состоянию каждый, то есть 14 состояний.
состоянию каждый, то есть 14 состояний.
Используя программу расчета -ATMOS, получаем следующие результаты, показанные в Таблице 10.4 и Таблице 10.5. Полные потери могут быть разбиты на потери из-за ограничения класса ( 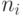 ) и потери из-за ограниченного числа каналов (
) и потери из-за ограниченного числа каналов (  ).
).
| Вход | Общее число каналов  |
|||||||
|---|---|---|---|---|---|---|---|---|
| Предложенная нагрузка | Пиковость | Максимальное размещение | Размер слота | Среднее время пребывания в системе | Источники | Бета | ||
 |
 |
 |
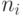 |
 |
 |
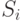 |
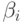 |
|
| 1 | 2.0000 | 1.00 | 6 | 1 | 1.00 |  |
0 | |
| 2 | 2.0000 | 0.75 | 6 | 2 | 1.00 | 4 | 0.3333 | |
| 3 | 1.0000 | 1.50 | 4 | 1 | 1.00 | -2 | -0.3333 | |
Потери по времени, потери по нагрузке, обслуженная нагрузка на выходе:
| Выход | Потери по вызовам | Потери по нагрузке | Потери по времени | Обслуженная нагрузка |
|---|---|---|---|---|
 |
 |
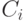 |
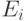 |
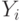 |
| 1 | 1.769 200E-01 | 1.769 200E-01 | 1.769 200E-01 | 1.646 160 |
| 2 | 3.346 853E-01 | 2.739 344E-01 | 3.836 316E-01 | 1.452 131 |
| 3 | 2.127 890E-01 | 2.884 898E-01 | 1.817 079E-01 | 0.711 510 |
| Итого | 2.380 397E-01 | 3.809 801 |

 источника
источника вызова/единица времени
вызова/единица времени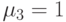 (единица времени -1)
(единица времени -1) Эрл. на свободный источник
Эрл. на свободный источник
 канал/вызов
канал/вызов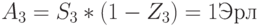
 (максимальное # одновременные вызовы)
(максимальное # одновременные вызовы)