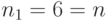|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Многомерные системы с потерями
Обратимые марковские процессы
В предыдущей секции мы рассматривали двухмерную диаграмму переходов состояний. Для увеличивающегося числа потоков нагрузки число состояний (и следовательно уравнений) увеличивается очень быстро. Однако, можно упростить проблему, используя структуру диаграммы переходов состояний. Рассмотрим двухмерную диаграмму переходов состояний, показанную в рис. 10.2. Для четырех соседних состояний поток в направлении по часовой стрелке должен равняться потоку в противоположном направлении (Kingman, 1969 [64]), (Sutton, 1980 [95]). Взглянем на рис. 10.2.
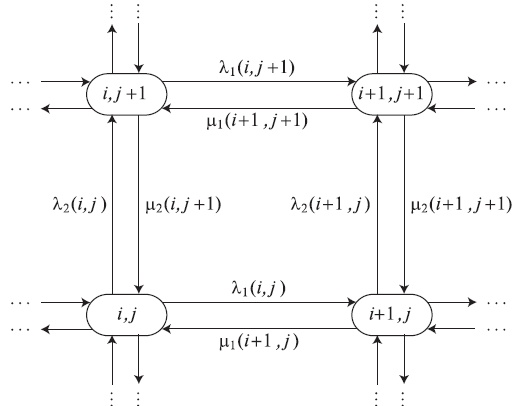
Рис. 10.2. Критерии Колмогорова - необходимое и достаточное условие для обратимости двухмерного марковского процесса: циркулирующий поток среди четырех соседних состояний в этом квадрате равняется нулю. Поток по часовой стрелке равняется потоку против часовой стрелки (10.12).
По часовой стрелке:
![[i,j] \to [i ,j+1]: p((i ,j)* \lambda_2 (i ,j)\\
[i ,j +1] \to [i+1 ,j+1]: p(i ,j +1)*\lambda_1(i ,j +1)\\
[i+1 ,j+1] \to [i+1 ,j]: p(i+1 ,j+1)*\mu_2(i+1 ,j+1)\\
[i+1 ,j] \to [i ,j]: p(i+1,j)*\mu_1(i+1,j),](/sites/default/files/tex_cache/8dcd0d5f6dd29a616d7cbc699bb1736f.png)
Против часовой стрелки:
![[i,j] \to [i+1 ,j]: \qquad p(i ,j)* \lambda_1 (i ,j)\\
[i+1 ,j ] \to [i+1 ,j+1]: \qquad p(i+1 ,j)*\lambda_2(i+1 ,j )\\
[i+1 ,j+1] \to [i ,j+1]: \qquad p(i+1 ,j+1)*\mu_1(i+1 ,j+1)\\
[i ,j+1] \to [i ,j]: \qquad p(i,j+1)*\mu_2(i,j+1)](/sites/default/files/tex_cache/d14f8abf913c9acec8a030097bd23065.png)
Мы можем сократить оба выражения на вероятности состояния и затем получить условие (10.12). Необходимое и достаточное условие для обратимости - что следующие два выражения являются равными.
По часовой стрелке:
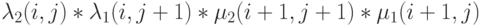 |
( 10.12) |
Против часовой стрелки:
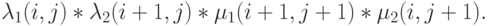
Если эти два выражения равны, то имеется локальное или частичное равновесие. Таким образом, необходимым условием для обратимости является то, что если есть поток (стрелка) от состояния i к состоянию j, тогда должен также быть поток (стрелка) от состояния j до состояния i. Мы можем применить уравнения сечения между любыми двумя подключенными состояниями. Итак, из рисунка 10.2 мы получаем:
 |
( 10.13) |
Мы можем выразить любую вероятность состояния  с помощью вероятности состояния
с помощью вероятности состояния  , выбирая любой путь между этими двумя состояниями ( критерии Колмогорова ). Мы можем, например, выбрать путь:
, выбирая любой путь между этими двумя состояниями ( критерии Колмогорова ). Мы можем, например, выбрать путь:
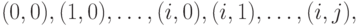
Тогда получаем следующее уравнение равновесия:
 |
( 10.15) |
Мы находим  нормировкой полной вероятности событий. Условие для обратимости будет выполнено во многих случаях, например, для:
нормировкой полной вероятности событий. Условие для обратимости будет выполнено во многих случаях, например, для:
 |
( 10.16) |
 |
( 10.17) |
Если мы рассматриваем многомерную систему с потерями, имеющую N потоков нагрузки, то любым потоком нагрузки может быть зависимый от состояния Пуассоновский процесс. В конкретном потоке могут быть нагрузки типа BPP (Бернулли, Пуассон, Паскаль). Для N - мерных систем условия обратимости аналогичны (10.12). Критерий Колмогорова должен выполняться для всех возможных путей. Практически, мы не испытываем никаких проблем, потому что решение, полученное согласно предположению об обратимости, будет правильным решением тогда и только тогда, когда выполнены уравнения равновесия узла. В следующей секции мы используем это как основание, чтобы ввести общую многомерную модель нагрузки.
Многомерные Системы с потерями
В этой секции мы рассматриваем обобщения классической теории телетрафика для систем, которые состоят из нескольких типов потоков нагрузки, поступающих на единственный канал или группу каналов или пучков каналов. Каждый поток нагрузки может иметь отдельные параметры и может быть зависимыми от состояния Пуассоновскими потоками вызовов с ограниченными классами и мультислотовым трафиком. Этот общий класс моделей нечувствителен к распределению времени пребывания в системе, которое может быть классом. Мы вводим обобщения по одному и представляем маленькое социологическое исследование, чтобы проиллюстрировать основные идеи.
Ограничение класса
По сравнению со случаем, который рассматривают в секции 10.1, мы теперь ограничим число одновременных запросов для каждого потока нагрузки (класса). Таким образом, не будет полной доступности, но в отличие от систем перегрузки, где физически существует доступ только к заданным каналам, теперь возможно использование всех каналов, но в любой момент мы можем занять только ограниченное их число. Это обеспечивает сервисная защита (защита числа виртуальных каналов = ограничение на класс обслуживания = приоритетная пороговая стратегия). Таким образом, мы вводим ограничения числа одновременных вызовов в классе j следующим образом:
 |
( 10.18) |
где
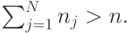
Если последнее ограничение не выполнено, то мы получаем отдельные группы, соответствующие N обычным независимым одномерным системам с потерями. Из-за ограничений диаграмма переходов состояний усечена. Для двух потоков нагрузки она показана на рис.10.3.
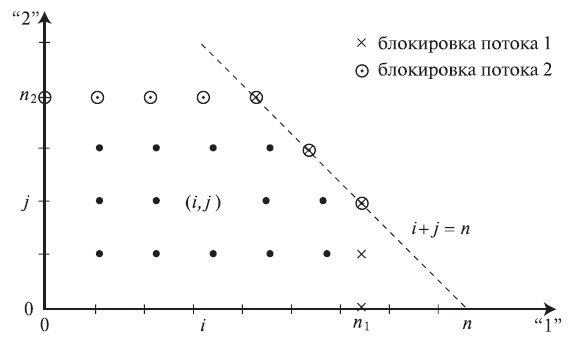
Рис. 10.3. Структура диаграммы переходов состояний для двухмерной нагрузки, обрабатываемая с ограничениями класса (см. 10.18). При вычислении вероятностей равновесия состояние (i, j) может быть выражено состоянием (i, j-1), рекурсивно состоянием (1, 0), (i-1, 0) и, наконец (0, 0) (см.10.15)
Заметим, что усеченная диаграмма переходов состояний все еще является обратимой и что значение p(i, j) относительно значения  при усечении не изменяется. Изменяется только нормировочная константа. Фактически, из-за локального свойства равновесия мы можем удалить любое состояние, не изменяя вышеупомянутые свойства. Можно рассмотреть больше общих ограничений класса к наборам потоков нагрузки так, чтобы любой поток нагрузки имел минимум (гарантируемый) числа распределенных каналов.
при усечении не изменяется. Изменяется только нормировочная константа. Фактически, из-за локального свойства равновесия мы можем удалить любое состояние, не изменяя вышеупомянутые свойства. Можно рассмотреть больше общих ограничений класса к наборам потоков нагрузки так, чтобы любой поток нагрузки имел минимум (гарантируемый) числа распределенных каналов.
Обобщенные процессы обслуживания нагрузки
Мы можем рассматривать PCT-I нагрузку только как в секции 10.1. Каждый поток нагрузки может быть зависимым от состояния, например, Пуассоновский поток вызовов с линейной зависимостью от состояния и своей скоростью выхода из системы (гибели), см. (10.16) и (10.17)
Система удовлетворяет условиям обратимости, см. (10.12). Таким образом, форма произведения также существует для BPP -потоков нагрузки и более общих Пуассоновских процессов, зависимых от состояния. Если все потоки нагрузки - энгсетовские (Биноминальные) процессы, то мы получаем многомерную формулу Энгсета (Jensen, 1948). Как уже упомянуто выше, система нечувствительна к распределениям времени пребывания в системе. Каждый поток нагрузки может иметь свое собственное отдельное распределение времени пребывания в системе.
Мультислотовая нагрузка
В системах с интеграцией служб требуемая пропускная способность может зависеть от типа обслуживания. Например, для обслуживания телефонного соединения с передачей только речи требуется один канал (слот), тогда как, например, для передачи видеоизображения может потребоваться  каналов одновременно. Мы получаем дополнительные ограничения:
каналов одновременно. Мы получаем дополнительные ограничения:
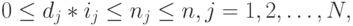 |
( 10.19) |
и
 |
( 10.20) |
где 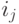 - фактическое число вызовов типа
- фактическое число вызовов типа  . Результирующая диаграмма переходов состояний будет обратима, и будет иметь форму произведения.
. Результирующая диаграмма переходов состояний будет обратима, и будет иметь форму произведения.
Ограничения соответствуют, например, физической модели, показанной в рис.10.5.
Предложенная нагрузка 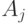 обычно определяется как среднее число попыток вызова на среднее время пребывания в системе. Если мы измеряем обслуженную нагрузку
обычно определяется как среднее число попыток вызова на среднее время пребывания в системе. Если мы измеряем обслуженную нагрузку 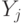 как среднее число занятых каналов, то потерянная нагрузка, измеренная в каналах, получается:
как среднее число занятых каналов, то потерянная нагрузка, измеренная в каналах, получается:
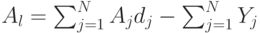 |
( 10.21) |

 вызова/единица времени
вызова/единица времени источника
источника вызова / в единицу времени / свободный источник
вызова / в единицу времени / свободный источник

 Эрл./свободный источник
Эрл./свободный источник (пиковость)
(пиковость) (пиковость)
(пиковость) канал/вызов
канал/вызов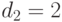 канал/вызов
канал/вызов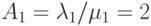 Эрл
Эрл Эрл
Эрл