|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Система с потерями и В-формула Эрланга
Пример 7.5.2: Вычисление EJA) для большого х
Применяя рекурсию, (7.30) мы находим:

Это выражение является обратной вероятностью блокировки В-формулы. При больших значениях х эта формула может быть применена для быстрого вычисления В-формулы, потому что мы можем ограничить сумму, когда ее элементы становятся очень маленькими.
Принципы измерения нагрузки
Когда измеряется нагрузка системы обслуживания, необходимо обеспечить баланс требований уровня обслуживания и экономических ограничений. В этой лекции мы увидим, как это может быть сделано.
В системах телекоммуникации есть несколько показателей, которые характеризуют обслуживание. Самый объемный показатель - Качество обслуживания ( QoS ). Он включает все аспекты соединения, такие, как качество речи, задержка информации, потери, надежность и т.д. Мы рассматриваем только небольшое подмножество этих аспектов: Уровень обслуживания ( GoS ) или сетевые рабочие характеристики включают аспекты, связанные только с емкостью сети.
После публикации формулы Эрланга в 1920 были установлены функциональные отношения между числом каналов, предложенной нагрузкой и уровнем обслуживания (вероятностью блокировки). Таким образом, были установлены показатели по качеству обслуживания нагрузки. Тогда существовали прямые линии между всеми станциями в области Копенгагена по группам направлений.
Если зафиксировать значение потерь нагрузки от блокировки по всем направлениям, то применение В-формулы Эрланга для слежения за нагрузкой по направлениям было бы ограниченным.
Кай Мо (Kai Мое 1893-1949), который был главным инженером Копенгагенской Телефонной Компании, сделал некоторые количественные экономические оценки и издал несколько распоряжений, где он вводил критические соображения по связи коммерческих интересов и блокировок. Сегодня они известны, в математической экономике как принципы Мо. Самуэльсон (Р.А. Samuelson) позже привел подобные соображения в своей известной книге, первоначально изданной в 1947 г.
На основе работ Мо сформулированы фундаментальные принципы измерения нагрузки для телекоммуникационных системах как Принципы Мо (Jensen, 1950 [50]).
Измерение нагрузки с фиксированной вероятностью блокировки
Для хорошей работы система с потерями должна иметь показатели потерь (вероятности блокировок) на достаточно низком уровне. Практически число каналов  должно быть выбрано так, чтобы
должно быть выбрано так, чтобы 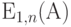 приблизительно было 1 %, чтобы избежать перегрузки из-за многих незаконченных вызовов и повторных попыток вызовов, которые перегружают систему и доставляют неприятности абонентам. [51]
приблизительно было 1 %, чтобы избежать перегрузки из-за многих незаконченных вызовов и повторных попыток вызовов, которые перегружают систему и доставляют неприятности абонентам. [51]
Таблица 7.1 показывает предложенную нагрузку для фиксированной вероятности блокировки Е=1% при некоторых значениях п.
Таблица также дает удельное использование каналов, которое принимает более высокое значение для больших групп. Если мы увеличиваем предложенную нагрузку на 20 % до  , то замечаем увеличение вероятности блокировки для всех значений
, то замечаем увеличение вероятности блокировки для всех значений  , но больше всего - для больших значений п.
, но больше всего - для больших значений п.
Общая стоимость для данного числа каналов тогда: (а) стоимость кабеля и (б) убытки из-за потерянной нагрузки (упущенный доход):
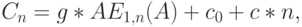 |
( 7.32) |
Здесь - А предложенная нагрузка, то есть потенциальный запрос на обслуживание нагрузки в рассматриваемой группе. Затраты из-за потерянной нагрузки уменьшаются с увеличением я, тогда как расходы из-за кабеля увеличиваются с увеличением п. Общая стоимость может иметь минимум для некоторого значения п. Практически п - целое число, и мы ищем значение n, для которого имеем (см. рис.7.6):
 и
и 
| n | 1 | 2 | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|---|---|
|
A(E=1%) a
|
0.010 0.010 0.000 |
0.153 0.076 0.001 |
1.361 0.269 0.011 |
4.461 0.442 0.027 |
12.031 0.596 0.052 |
37.901 0.750 0.099 |
84.064 0.832 0.147 |
|
E[%] a
|
0.012 1.198 0.012 0.000 |
0.183 1.396 0.090 0.002 |
1.633 1.903 0.320 0.023 |
5.353 2.575 0.522 0.072 |
14.437 3.640 0.696 0.173 |
45.482 5.848 0.856 0.405 |
100.877 8.077 0.927 0.617 |
 |
1 | 2 | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|---|---|
|
|
0.271 0.213 21.29 |
0.607 0.272 10.28 |
2.009 0.387 3.72 |
4.991 0.490 1.82 |
11.98 0.593 0.97 |
35.80 0.713 0.47 |
78.73 0.785 0.29 |
|
A{%} a
|
0.325 24.51 0.245 0.067 |
0.728 13.30 0.316 0.074 |
2.411 6.32 0.452 0.093 |
5.989 4.28 0.573 0.120 |
14.38 3.55 0.693 0.169 |
42.96 3.73 0.827 0.294 |
94.476 4.62 0.901 0.452 |

Рис. 7.6. Общая стоимость состоит из затрат на кабель и упущенного дохода из-за блокировок нагрузки (7.32).
Минимум общей стоимости получается, когда выполняется неравенство (7.33), то есть когда две функции стоимости имеют тот же самый наклон с противоположными знаками (квант приращения). (  ). Минимум получен для n = 30 каналов
). Минимум получен для n = 30 каналов
При 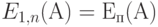 мы имеем
мы имеем
 |
( 7.33) |
 |
( 7.34) |
где
 |
( 7.35) |
 называется значением выигрыша. Заметим, что
называется значением выигрыша. Заметим, что 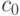 не входит в условие минимума. Это значение определяет, выгодно ли передавать нагрузку вообще. Мы должны потребовать, что для некоторого положительного значения п выполняется неравенство:
не входит в условие минимума. Это значение определяет, выгодно ли передавать нагрузку вообще. Мы должны потребовать, что для некоторого положительного значения п выполняется неравенство:
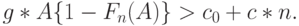 |
( 7.36) |
Pис.7.7 показывает вероятности блокировки для некоторых значений  . Отметим, что экономический расчет на прибыль в некотором смысле заложен в значении выигрыша. Практически мы выбираем
. Отметим, что экономический расчет на прибыль в некотором смысле заложен в значении выигрыша. Практически мы выбираем  частично независимо от функции стоимости.
частично независимо от функции стоимости.
В Дании использовались следующие значения:
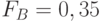 для первичных групп каналов;
для первичных групп каналов;
 для обслуживания резервных первичных групп. (7.37);
для обслуживания резервных первичных групп. (7.37);
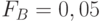 для групп без альтернативного маршрута.
для групп без альтернативного маршрута.
Случай, когда размерность вероятности блокировки нагрузки с фиксированным значением значения выигрыша  для малых значений предложенной нагрузки становится большим (см. таблицу. 7.2)
для малых значений предложенной нагрузки становится большим (см. таблицу. 7.2)
Краткие итоги
- В-формула Эрланга основана на модели, которая содержит три элемента: структура, стратегия и нагрузка.
- Мы рассматриваем систему из п идентичных обслуживающих приборов (серверы, каналы, слоты), работающих параллельно.
- Вызов, достигая системы, принимается для обслуживания, если, по крайней мере, один канал свободен. Если все каналы заняты, система переполняется, и попытка вызова блокируется.
- Принимается, что времена обслуживания являются экспоненциально распределенными с интенсивностью
 . Процесс поступления вызовов - Пуассоновский процесс со скоростью
. Процесс поступления вызовов - Пуассоновский процесс со скоростью  .
. - Предполагается, что предложенная нагрузка поступает при бесконечном числе каналов.
- Самые важные показатели уровня обслуживания для систем с потерями - потери по времени Е, потери по вызовам В, и потери по нагрузке С.
- Состояние системы, [i], как число занятых каналов i (i = 0; 1; 2,...). Все состояния системы показаны в виде окружностей и дуг от одного состояния до другого состояния, на которых приведены значения интенсивности.
- Предполагается, что система находится в статистическом равновесии. В статистическом равновесии число в единицу времен переходов в состояние [i] равно числу переходов из состояния [i].
- Будущее развитие диаграммы состояний зависит только от существующего состояния, а не от того, как процесс прибыл в это состояние (марковское свойство).
-
Во многих случаях мы можем применять простую структуру диаграммы перехода состояния. Применим фиктивное сечение, например, между состоянием [i-1] и [i] (т.е. выделяем переходы от состояния [0]; [1].... [i-1]). Затем рассматриваем в статистическое равновесие нагрузки от состояния [i-1] к [i] и изменение от состояния [i] к [i-1]
- Число занятых каналов в случайный момент времени подчиняется Пуассоновскому распределению, число вызовов в фиксированном временном интервале также подчиняется Пуассоновскому распределению.
- Усеченное Пуассоновское распределение (первая формула Эрланга) -это такое распределение, для которого пространство состояний ограничено {0; 1,... n}.
-
Потери по времени: вероятность, что все п каналов заняты в случайный момент времени.
Потери по вызовам: вероятность, что случайный вызов будет потерян.
Потери по нагрузке: разность между предложенной и потерянной нагрузкой.
Для всех систем с Пуассоновскими потоками вызовов эти характеристики равны.
- Нагрузка, которую несет i - ый канал (использование
 ), зависит от типа поиска.
), зависит от типа поиска. - Функция увеличения обозначает увеличение обслуженной нагрузки, когда число каналов увеличено на один от п до п + 1.
- Стандартная процедура моделирования задач посредством применения диаграмм перехода состояния состоит из множества шагов и может быть сформулирована в общих терминах. Эта процедура также применима для многомерных диаграмм перехода состояния.
- Для вычислений формула Эрланга не является удобной: n! увеличивается так быстро, что в компьютере возникает перегрузка, поэтому на практике применяется рекурсивная формула.
- Когда измеряется нагрузка системы обслуживания, мы должны обеспечить баланс требований уровня обслуживания и экономических ограничений.
- Самый объемный показатель - Качество обслуживания, ( QoS ). Он включает все аспекты соединения, такие, как качество речи, задержка информации, потери, надежность и т.д. Уровень обслуживания ( GoS ) или сетевые рабочие характеристики включают аспекты, связанные только с емкостью сети.
- На основе работ Мо сформулированы фундаментальные принципы измерения нагрузки для телекоммуникационных системах как Принципы Мо
- Общая стоимость для данного числа каналов - стоимость кабеля и убыль из-за потерянной нагрузки (упущенный доход).

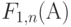 (7.16) для фиксированного значения вероятности блокировки
(7.16) для фиксированного значения вероятности блокировки 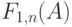




![E_{1,n}(A)[\%]](/sites/default/files/tex_cache/74f1b9b98b4434b668346889fb966ca9.png)
