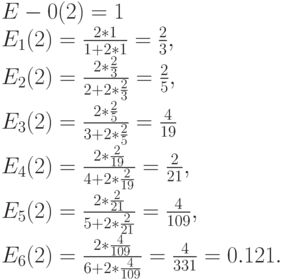|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Система с потерями и В-формула Эрланга
Общая процедура для диаграмм перехода состояний
Самый важный инструмент в теории телетрафика - формулировка и решение задач с помощью моделей, посредством применения диаграмм перехода состояния. Из предыдущих секций мы можем установить следующую стандартную процедуру для того, чтобы применить диаграмму перехода состояния. Она состоит из множества шагов и может быть сформулирована в общих терминах. Эта процедура также применима для многомерных диаграмм перехода состояния, которые мы рассмотрим позже.
Процедура всегда проходит следующие шаги.
-
Созданием диаграммы перехода состояния:
- определяют состояния системы,
- рисуют состояния как окружности,
- рассматривают состояния по одному и вводят в рисунок все возможные стрелки переходов от одного состояния к другому. При этом учитывают следующие процессы:
- процесс поступления вызовов (вновь прибывшая заявка или сдвиг фаз в процессе поступления вызовов),
- процесс окончания (время окончания обслуживания или сдвиг фазы).
Этим способом мы получаем законченную диаграмму перехода состояния.
-
Составить уравнения, описывающие систему.
Если условия для статистического равновесия выполнены, уравнения устойчивости состояний могут быть получены из:
- уравнений узла,
- уравнения сечения.
-
Решить уравнения равновесия, отображающие статистическое равновесие.
- выражают все вероятности состояния, например, с помощью вероятности нулевого состояния
![[0] -р(0)](/sites/default/files/tex_cache/4eed7699b29ea759ae629ec1d0e5c9fd.png) ,
, - нормализацией находят
 .
.
- выражают все вероятности состояния, например, с помощью вероятности нулевого состояния
- Вычислить критерии качества работы, выраженные вероятностями состояния.
На практике мы находим ненормализованное значение вероятности состояния  , равное единице, а затем вычисляем относительную величину
, равное единице, а затем вычисляем относительную величину  . Нормализуя ее, находим:
. Нормализуя ее, находим:
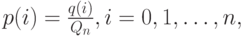 |
( 7.19) |
где
 |
( 7.20) |
Тогда потери по времени получаются равными:
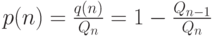 |
( 7.21) |
Рекурсивная формула
Если значения 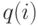 становятся очень большими (например,
становятся очень большими (например, 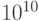 ), то мы можем умножить все
), то мы можем умножить все 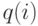 на одну и ту константу (например,
на одну и ту константу (например,  ), так как мы знаем, что все значения вероятностей находятся в пределах интервала [0, 1]. Этим способом мы избегаем проблем вычисления. Если значения
), так как мы знаем, что все значения вероятностей находятся в пределах интервала [0, 1]. Этим способом мы избегаем проблем вычисления. Если значения 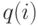 становятся очень маленькими, мы можем усечь пространство состояний, так как плотность распределения
становятся очень маленькими, мы можем усечь пространство состояний, так как плотность распределения 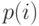 часто имеет колоколоо-бразный вид
часто имеет колоколоо-бразный вид  (unimodal - "унимодальный") и поэтому имеет максимум. Во многих случаях мы, теоретически, способны контролировать ошибку, вносимую усечением пространства состояний (Степанов, 1989 [94]).
(unimodal - "унимодальный") и поэтому имеет максимум. Во многих случаях мы, теоретически, способны контролировать ошибку, вносимую усечением пространства состояний (Степанов, 1989 [94]).
Мы можем нормализовать вероятности состояний после каждого шага, который требует больших вычислений, но гарантирует высокую точность. Нормализуем вероятности состояний для системы с  каналами:
каналами:
 |
( 7.22) |
где индекс  указывает, что это вероятности состояния для системы с
указывает, что это вероятности состояния для системы с  каналом. Предположим, что мы имеем следующую рекурсию для
каналом. Предположим, что мы имеем следующую рекурсию для  , заданную некоторой функцией от предыдущих вероятностей состояний:
, заданную некоторой функцией от предыдущих вероятностей состояний:
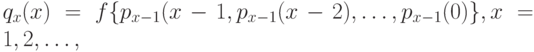 |
( 7.23) |
где  будет относительной вероятностью состояния. Предположим, что мы знаем нормализованные вероятности состояний для
будет относительной вероятностью состояния. Предположим, что мы знаем нормализованные вероятности состояний для  каналов (7.22) и хотим найти нормализованные вероятности состояния для системы с
каналов (7.22) и хотим найти нормализованные вероятности состояния для системы с  каналами. Относительные значения вероятностей состояния не изменяются, когда мы увеличиваем число каналов на один, тогда получаем:
каналами. Относительные значения вероятностей состояния не изменяются, когда мы увеличиваем число каналов на один, тогда получаем:
 |
( 7.24) |
Новая константа нормализации получается:
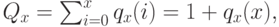
так как мы на предыдущем шаге нормализовали сумму вероятностей состояний в пределах от 0 к  , и, увеличивая их на единицу, получаем:
, и, увеличивая их на единицу, получаем:
 |
( 7.25) |
В начале процесса рекурсии присваивается значение 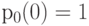 . Алгоритм рекурсии начинается с этого значения и находит вероятности состояния системы с одним каналом больше (7.24) и (7.25). Рекурсия в цифровой форме очень устойчива, потому что мы в (7.25) делим на число, большее единицы.
. Алгоритм рекурсии начинается с этого значения и находит вероятности состояния системы с одним каналом больше (7.24) и (7.25). Рекурсия в цифровой форме очень устойчива, потому что мы в (7.25) делим на число, большее единицы.
Рассмотрим простой процесс гибели и размножения с интенсивностью поступления 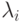 и скоростью выхода из состояния
и скоростью выхода из состояния  в состоянии
в состоянии  . Тогда
. Тогда  зависит только от вероятности предыдущего состояния. Используя уравнение сечения, мы получаем следующую формулу рекурсии:
зависит только от вероятности предыдущего состояния. Используя уравнение сечения, мы получаем следующую формулу рекурсии:
 |
( 7.26) |
Потери по времени для  каналов -
каналов -  . Подставляя (7.26) в (7.25), получаем простую рекурсивную формулу для потерь по времени:
. Подставляя (7.26) в (7.25), получаем простую рекурсивную формулу для потерь по времени:
 |
( 7.27) |
Находя инверсию вероятности потерь по времени 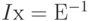 , мы получаем:
, мы получаем:
 |
( 7.28) |
Это общая рекурсивная формула для вычисления потерь по времени для всех систем с интенсивностью поступления состояния 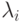 и однородными обслуживающими приборами.
и однородными обслуживающими приборами.
Пример 7.4.1: Вычисление вероятностей Пуассоновского распределения
Если мы хотим вычислить Пуассоновское распределение (7.6) для очень больших средних величин  , тогда полезно предположить, что
, тогда полезно предположить, что  , где
, где  равен целой части от
равен целой части от  . Относительные значения
. Относительные значения 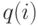 для уменьшающихся значений
для уменьшающихся значений  и для увеличивающихся значений
и для увеличивающихся значений  будет тогда уменьшаться, и мы можем остановить вычисления, когда, например,
будет тогда уменьшаться, и мы можем остановить вычисления, когда, например,  и, наконец, нормализуют
и, наконец, нормализуют 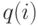 . Практически не будет никаких проблем нормализовать вероятности. Более строгий подход состоит в том, чтобы использовать вышеупомянутую формулу рекурсии.
. Практически не будет никаких проблем нормализовать вероятности. Более строгий подход состоит в том, чтобы использовать вышеупомянутую формулу рекурсии.
Расчет по В-формуле Эрланга
Для вычислений формула (7.10) не является удобной:  ! увеличивается так быстро, что в компьютере возникает перегрузка. Если мы применим (7.27), то получим рекурсивную формулу:
! увеличивается так быстро, что в компьютере возникает перегрузка. Если мы применим (7.27), то получим рекурсивную формулу:
 |
( 7.29) |
С числовой точки зрения, линейная форма (7.28) самая устойчивая:
 |
( 7.30) |
где  . Эта рекурсивная формула точна, и даже для больших значений
. Эта рекурсивная формула точна, и даже для больших значений  нет ошибок округления. Это - основная формула для многочисленных таблиц В-формул Эрланга и так называемых классических таблиц (Пальма, 1947 [81] ). Для очень больших значений
нет ошибок округления. Это - основная формула для многочисленных таблиц В-формул Эрланга и так называемых классических таблиц (Пальма, 1947 [81] ). Для очень больших значений  есть более эффективные алгоритмы. Заметим, что рекурсивная формула, которая является точной при увеличении индекса, обычно неточна при уменьшении индекса, и наоборот.
есть более эффективные алгоритмы. Заметим, что рекурсивная формула, которая является точной при увеличении индекса, обычно неточна при уменьшении индекса, и наоборот.
Пример 7.5.1: Эрланговская система с потерями
Мы рассматриваем Эрланговскую систему с потерями с  каналами, интенсивностью поступления вызовов
каналами, интенсивностью поступления вызовов  в единицу времени и интенсивностью освобождения
в единицу времени и интенсивностью освобождения 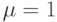 в единицу времени отклонения так, чтобы предложенная нагрузка была
в единицу времени отклонения так, чтобы предложенная нагрузка была 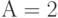 Эрл. Если мы обозначим ненормализованную вероятность относительного состояния
Эрл. Если мы обозначим ненормализованную вероятность относительного состояния 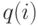 , то получим диаграмму перехода состояния, которая схематически изображает значения, показанные в следующей таблице:
, то получим диаграмму перехода состояния, которая схематически изображает значения, показанные в следующей таблице:
 |
 |
 |
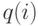 |
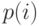 |
 |
 |
|---|---|---|---|---|---|---|
| 0 | 2 | 0 | 1.0000 | 0.1360 | 0.0000 | 0.2719 |
| 1 | 2 | 1 | 2.0000 | 0.2719 | 0.2719 | 0.5438 |
| 2 | 2 | 2 | 2.0000 | 0.2719 | 0.5438 | 0.5438 |
| 3 | 2 | 3 | 1.3333 | 0.1813 | 0.5438 | 0.3625 |
| 4 | 2 | 4 | 0.6667 | 0.0906 | 0.3625 | 0.1813 |
| 5 | 2 | 5 | 0.2667 | 0.0363 | 0.1817 | 0.0725 |
| 6 | 2 | 6 | 0.0889 | 0.0121 | 0.0725 | 0.0242 |
| Total | 7.3556 | 1.0000 | 1.9758 | 2.0000 |
Мы получаем следующие вероятности блокировки:
Потери по времени  .
.
Потери по нагрузке  .
.
Потери по вызовам  .
.
Отметим, что  из-за свойства PASTA (Poisson Arrival See Time Average - Пуассоновское поступление вызовов, наблюдаемое за среднее время).
из-за свойства PASTA (Poisson Arrival See Time Average - Пуассоновское поступление вызовов, наблюдаемое за среднее время).
Применяя рекурсивную формулу (7.29), мы, конечно, получаем те же самые результаты