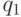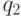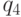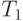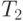|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Организация компьютерных экспериментов
7.3. Дисперсионный анализ (отсеивающий эксперимент). Обратная задача
7.3.1. Постановка задачи
Изготовление в цехе детали начинается через случайное время 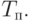 Выполнению операций предшествует подготовка. Длительность подготовки зависит от качества заготовки, из которой будет сделана деталь. Всего различных видов заготовок
Выполнению операций предшествует подготовка. Длительность подготовки зависит от качества заготовки, из которой будет сделана деталь. Всего различных видов заготовок 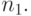 Время подготовки подчинено экспоненциальному закону. Частота появления различных заготовок и средние значения времени их подготовки заданы табл. 7.2 дискретного распределения:
Время подготовки подчинено экспоненциальному закону. Частота появления различных заготовок и средние значения времени их подготовки заданы табл. 7.2 дискретного распределения:
Для изготовления детали последовательно выполняются  операций, продолжительностями
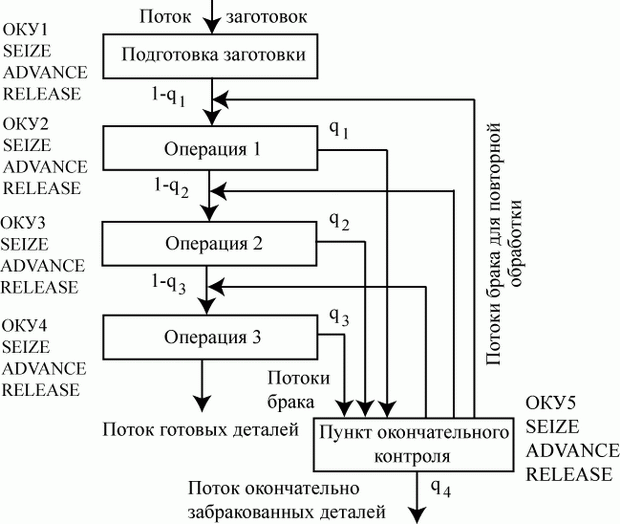
операций, продолжительностями 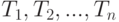 соответственно. После каждой операции в течение времени
соответственно. После каждой операции в течение времени 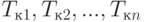 следует контроль. Время выполнения операций и контроля - случайное. Контроль не проходят
следует контроль. Время выполнения операций и контроля - случайное. Контроль не проходят 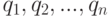 деталей соответственно.
деталей соответственно.
Забракованные детали поступают на пункт окончательного контроля и проходят на нем проверку в течение случайного времени 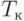 . В результате из общего количества не прошедших контроль деталей
. В результате из общего количества не прошедших контроль деталей 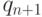 идут в брак, а оставшиеся
идут в брак, а оставшиеся 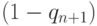 деталей подлежат повторному выполнению операций, после которых они не прошли контроль. Если деталь во второй раз не проходит контроль, она окончательно бракуется.
деталей подлежат повторному выполнению операций, после которых они не прошли контроль. Если деталь во второй раз не проходит контроль, она окончательно бракуется.
7.3.2. Исходные данные
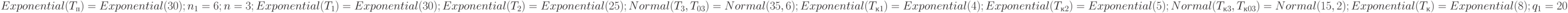
7.3.3. Задание на исследование
Разработать имитационную модель процесса изготовления в цехе деталей.
Вариант 1. Исследовать влияние качества выполнения операций 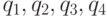 на время изготовления
на время изготовления  деталей (табл. 7.3). Результаты моделирования необходимо получить с точностью
деталей (табл. 7.3). Результаты моделирования необходимо получить с точностью 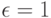 мин и доверительной вероятностью
мин и доверительной вероятностью 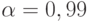 .
.
Вариант 2. Исследовать влияние интервалов времени 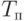 поступления заготовок и времени
поступления заготовок и времени 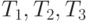 выполнения операций 1, 2, 3 соответственно на время подготовки
выполнения операций 1, 2, 3 соответственно на время подготовки 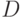 деталей (табл. 7.4). Результаты моделирования также необходимо получить с точностью
деталей (табл. 7.4). Результаты моделирования также необходимо получить с точностью  мин и доверительной вероятностью
мин и доверительной вероятностью 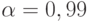 .
.
Модель должна также позволять определять относительное количество готовых и забракованных деталей, среднее время изготовления одной детали. Сделать выводы о загруженности пунктов выполнения операций и необходимых мерах по сокращению времени изготовления деталей.
7.3.4. Уяснение задачи на исследование
Процесс изготовления в цехе деталей представляет собой процесс, протекающий в многофазной разомкнутой системе массового обслуживания с ожиданием ( рис. 7.13).
Представим, что подготовка заготовки и операции 1, 2 и 3 производятся на станках - ОКУ 1, 2, 3 и 4 соответственно. Пункт окончательного контроля можно также представить ОКУ. Необходимые для их имитации средства GPSS приведены на рис. 7.13.
Время подготовки заготовки и время выполнения операций даны в мин. Возьмем 1 ед. мод. вр. = 1мин. Для расчета количества прогонов модели примем, что среднее квадратическое отклонение времени изготовления  деталей
деталей 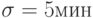 . Тогда
. Тогда
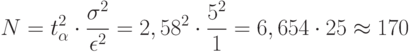
Программа модели обратной задачи приведена ниже.
7.3.5. Программа модели
; Модель изготовления деталей. Обратная задача ; Задание исходных данных Tn_ EQU 35 ; Среднее время между поступлениями заготовок T1 EQU 30 ; Среднее время выполнения 1-й операции, мин T2 EQU 25 ; Среднее время выполнения 2-й операции, мин T3 EQU 35 ; Среднее время выполнения 3-й операции, мин To3 EQU 6 ; Среднеквадратическое отклонение времени выполнения 3-й операции, мин Tk1 EQU 4 ; Среднее время контроля после 1-й операции, мин Tk2 EQU 5 ; Среднее время контроля после 2-й операции, мин Tk3 EQU 15 ; Среднее время контроля после 3-й операции, мин Tok3 EQU 2 ; Среднеквадратическое отклонение времени контроля после 3-й операции, мин Tk EQU 8 ; Среднее время окончательного контроля, мин q1_ EQU .12 ; Доля брака после 1-й операции q2_ EQU .15 ; Доля брака после 2-й операции q3_ EQU .10 ; Доля брака после 3-й операции q4_ EQU .80 ; Доля окончательного брака Det EQU 4 ; Количество деталей, которые нужно изготовить ; Описание функции времени подготовки заготовок для детали Pod FUNCTION RN10,D6 .05,10/.18,14/.34,21/.56,22/.85,28/1,25 ; Сегмент имитации изготовления деталей GENERATE (Exponential(1,0,Tn_)) ; Источник заготовок ; Подготовка заготовок для деталей QUEUE Pod ; Встать в очередь SEIZE Pod ; Начать подготовку заготовки DEPART Pod ; Покинуть очередь ADVANCE (Exponential(34,0,FN$Pod)) ; Имитация подготовки RELEASE Pod ; Закончить подготовку заготовки ; Имитация выполнения 1-й операции DCount ASSIGN 1,1 ; Код 1 в Р1-деталь проходит первый раз ASSIGN 2,1 ; Код 1 в Р2-признак 1-й операции Oper1 QUEUE P2 ; Встать в очередь SEIZE Konveer1 ; Начать первую операцию DEPART P2 ; Покинуть очередь ADVANCE (Exponential(23,0,T1)) ; Имитация 1-й операции RELEASE Konveer1 ; Закончить 1-ю операцию ADVANCE (Exponential(23,0,Tk1)) ; Контроль 1-й операции TRANSFER q1_,,Sboi ; Отправить брак на пункт контроля ; Имитация выполнения 2-й операции ASSIGN 2,2 ; Код 2 в Р2-признак 2-й операции Oper2 QUEUE P2 ; Встать в очередь SEIZE Konveer2 ; Начать вторую операцию DEPART P2 ; Покинуть очередь ADVANCE (Exponential(23,0,T2)) ; Имитация 2-й операции RELEASE Konveer2 ; Закончить 2-ю операцию ADVANCE (Exponential(23,0,Tk2)) ; Контроль 2-й операции TRANSFER q2_,,Sboi ; Отправить брак на пункт контроля ; Имитация выполнения 3-й операции ASSIGN 2,3 ; Код 3 в Р2-признак 3-й операции Oper3 QUEUE P2 ; Встать в очередь SEIZE Konveer3 ; Начать третью операцию DEPART P2 ; Покинуть очередь ADVANCE (Normal(20,(T3#K1),(To3#K1))) ; Имитация 3-й операции RELEASE Konveer3 ; Закончить 3-ю операцию ADVANCE (Normal(20,Tk3,Tok3)) ; Контроль 3-й операции TRANSFER q3_,,Sboi ; Отправить брак на пункт контроля TRANSFER ,Met2 ; Готовые детали ; Сегмент имитации работы пункта контроля Sboi QUEUE Kont ; Встать в очередь на пункт контроля SEIZE Kontr ; Занять пункт контроля DEPART Kont ; Покинуть очередь на пункт контроля ADVANCE (Exponential(23,0,Tk)) ; Окончательный контроль RELEASE Kontr ; Освободить пункт контроля TRANSFER q4_,,EndOper ; Отправить в окончательный брак TEST E P1,1,EndOper; Если второй раз, то в окончательный брак ASSIGN 1,2 ; Код 2 в Р1-деталь проходит второй раз Met1 TRANSFER ,(Met1+P2) TRANSFER ,Oper1 ; На повторное выполнение 1-й операции TRANSFER ,Oper2 ; На повторное выполнение 2-й операции TRANSFER ,Oper3 ; На повторное выполнение 3-й операции EndOper TERMINATE ; Счет брака ; Сегмент завершения моделирования и расчета результатов Met2 TEST L X$Prog,TG1,Met3 ; Если условие выполняется, то SAVEVALUE Prog,TG1 ; X$Prog=TG1 счетчику завершений SAVEVALUE NDet,0 ; Обнуление X$NDet Met3 SAVEVALUE NDet+,1 ; Счет количества готовых деталей TEST E X$NDet,Det,Ter1 ; Если готово Det деталей, зафиксировать один прогон TEST E TG1,1,Met4 ; Если содержимое счетчика завершений равно 1, то расчет результатов моделирования SAVEVALUE Brak,(INT(N$EndOper/X$Prog)) ; Количество забракованных деталей, шт. SAVEVALUE DoljaBrak,(X$Brak/(X$Brak+Det)) ; Общая доля брака SAVEVALUE DoljaDet,(Det/(X$Brak+Det)) ; Доля готовых деталей SAVEVALUE AC3,(AC1-X$AC2) SAVEVALUE TDet,((X$AC3/X$Prog)/60) ; Среднее время изготовления Det деталей, час SAVEVALUE SDet,((X$TDet/N_)#60) ; Среднее время изготовления одной детали, мин SAVEVALUE AC2,AC1 SAVEVALUE X$Prog,0 Met4 SAVEVALUE NDet,0 ; Обнуление X$NDet TERMINATE 1 ; Вычитание из счетчика завершений 1 Ter1 TERMINATE ; Вывод вспомогательных транзактов
Программа модели имеет достаточно подробный комментарий. Поэтому остановимся только на особенностях сегмента завершения моделирования и расчета результатов.
Поскольку результатом моделирования является оценка математического ожидания времени TDet изготовления Det деталей, то в ее вычислении используется абсолютное модельное время АС1 (системный числовой атрибут). При проведении дисперсионного анализа встроенный генератор эксперимента имеет две команды START, а между ними - команда RESET. Команда RESET не влияет на абсолютное модельное время. Поэтому АС1 будет суммой абсолютного модельного времени предварительных прогонов до установившегося режима, обозначим его АС2, и абсолютного модельного времени, пусть АС3, основных прогонов, в ходе которых собирается интересующая нас статистика. Нам для расчетов нужно АС3. Для его получения в программу введены строки:
SAVEVALUE AC3,(AC1-X$AC2) SAVEVALUE AC2,AC1
После предварительных прогонов в ячейке X$Prog сохранится указанное в первой команде START количество прогонов. Эта ячейка используется в первой строке рассматриваемого сегмента и ее содержимое должно быть равным нулю. В противном случае модель будет работать неверно. Для предотвращения ошибки введена строка:
SAVEVALUE X$Prog,0