|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Типовые математические модели
2.5. Моделирование СМО в классе непрерывных марковских процессов
Под операцией в СМО понимают комплекс мероприятий по обслуживанию входящего потока заявок на интервале времени  .
.
В зависимости от типа системы показателями исхода операции или эффективности системы массового обслуживания являются следующие.
Для СМО с отказами:
-
абсолютная пропускная способность (
 ) - среднее число заявок, обслуживаемое системой за время
) - среднее число заявок, обслуживаемое системой за время  ;
; -
относительная пропускная способность (
 ) - средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время
) - средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время  );
); -
среднее число занятых каналов (
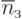 );
); -
коэффициент занятости (использования) каналов (
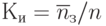 , где
, где  - число каналов в системе);
- число каналов в системе); -
коэффициент простоя каналов,
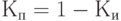 .
.
Для СМО с неограниченным ожиданием как абсолютная, так и относительная пропускная способности теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Для такой СМО важными показателями являются:
-
среднее число заявок в очереди (
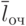 );
); -
среднее число заявок в системе (в очереди и на обслуживании,
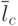 );
); -
среднее время ожидания заявки в очереди (
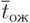 );
); -
среднее время пребывания заявки в системе (в очереди и на обслуживании,
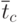 );
); -
коэффициенты использования и простоя каналов (
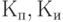 );
); -
среднее число свободных и занятых каналов (
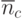 ,
, 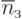 ).
).
Для СМО смешанного типа используются обе группы показателей: как относительная и абсолютная пропускная способности, так и характеристики ожидания.
В зависимости от цели операции массового обслуживания любой из приведенных показателей (или совокупность показателей) может быть выбран в качестве критерия эффективности.
Аналитической моделью СМО является совокупность уравнений или формул, позволяющих определять вероятности состояний системы в процессе ее функционирования и рассчитывать показатели эффективности по известным характеристикам входящего потока и каналов обслуживания.
Всеобщей аналитической модели для произвольной СМО не существует. Аналитические модели разработаны для ограниченного числа частных случаев СМО. Аналитические модели, более или менее точно отображающие реальные системы, как правило, сложны и труднообозримы.
Аналитическое моделирование СМО существенно облегчается, если процессы, протекающие в СМО, марковские (потоки заявок простейшие, времена обслуживания распределены экспоненциально). В этом случае все процессы в СМО можно описать обыкновенными дифференциальными уравнениями, а в предельном случае, для стационарных состояний - линейными алгебраическими уравнениями и, решив их, определить выбранные показатели эффективности.
Рассмотрим примеры некоторых СМО.
2.5.1. Многоканальная СМО с отказами
Пример 2.5. Три автоинспектора проверяют путевые листы у водителей грузовых автомобилей. Если хотя бы один инспектор свободен, проезжающий грузовик останавливают. Если все инспекторы заняты, грузовик, не задерживаясь, проезжает мимо. Поток грузовиков простейший, время проверки случайное с экспоненциальным распределением.
Такую ситуацию можно моделировать трехканальной СМО с отказами (без очереди). Система разомкнутая, с однородными заявками, однофазная, с абсолютно надежными каналами.
Описание состояний:
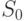 - все инспекторы свободны;
- все инспекторы свободны;
 - занят один инспектор;
- занят один инспектор;
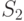 - заняты два инспектора;
- заняты два инспектора;
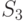 - заняты три инспектора.
- заняты три инспектора.
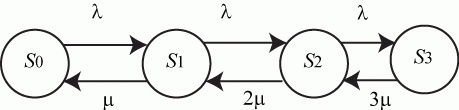
Граф состояний системы приведен на рис. 2.11.
На графе:  - интенсивность потока грузовых автомобилей;
- интенсивность потока грузовых автомобилей;  - интенсивность проверок документов одним автоинспектором.
- интенсивность проверок документов одним автоинспектором.
Моделирование проводится с целью определения части автомобилей, которые не будут проверены.
Решение
Искомая часть вероятности 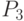 - вероятности занятости всех трех инспекторов. Поскольку граф состояний представляет типовую схему "гибели и размножения", то найдем
- вероятности занятости всех трех инспекторов. Поскольку граф состояний представляет типовую схему "гибели и размножения", то найдем 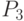 , используя зависимости (2.2).
, используя зависимости (2.2).
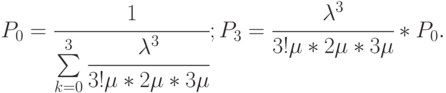
Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью:
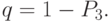
Пример 2.6. Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером - 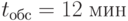 . Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
. Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.
Решение
Группа офицеров работает как СМО с отказами, состоящая из трех каналов.
Поток донесений с интенсивностью 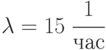 можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания
можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания 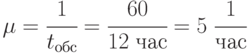 . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
. Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.
Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния:
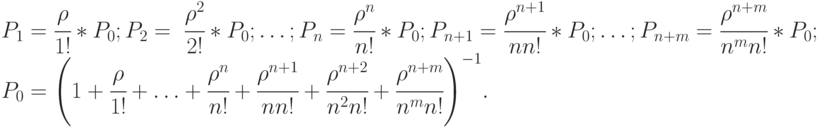
Отношение 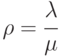 называют приведенной интенсивностью потока заявок. Физический смысл ее следующий: величина
называют приведенной интенсивностью потока заявок. Физический смысл ее следующий: величина  представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
В примере 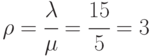 .
.
В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть 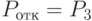 . Тогда:
. Тогда:
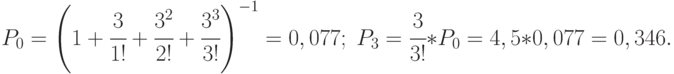
Так как вероятность отказа в обработке донесений составляет более 34 % ( 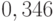 ), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем
), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем  :
:
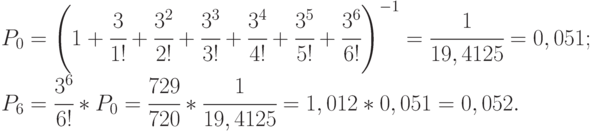
Теперь 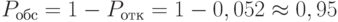 .
.
Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.
2.5.2. Многоканальная СМО с ожиданием
Пример 2.7. На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).
Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.
Решение
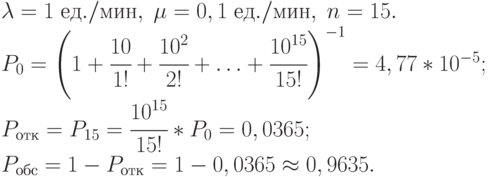
Абсолютная пропускная способность 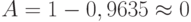 , т. е. все, что подходит к переправе, тут же практически переправляется.
, т. е. все, что подходит к переправе, тут же практически переправляется.
Среднее число работающих переправочных средств:
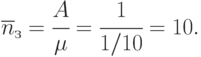
Коэффициенты использования и простоя переправы:
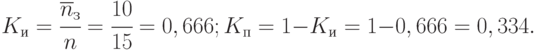
Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.
Коэффициенты использования переправы после 50 прогонов практически совпадают: 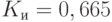 .
.
Максимальная длина очереди 15 ед., среднее время пребывания в очереди около 10 мин.
Если взять число переправочных средств 10, то коэффициент использования близок к 1 ( 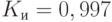 ), максимальная длина очереди - 43 единицы техники.
), максимальная длина очереди - 43 единицы техники.
2.5.3. Одноканальная СМО с ограниченной очередью
Если в очереди  мест для ожидания, то система может находиться в одном из следующих
мест для ожидания, то система может находиться в одном из следующих  состояний:
состояний:
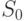 - в системе нет заявок (ни в очереди, ни на обслуживании);
- в системе нет заявок (ни в очереди, ни на обслуживании);
 - в системе обслуживается одна заявка, очередь пуста;
- в системе обслуживается одна заявка, очередь пуста;
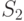 - в системе обслуживается одна заявка, и одна заявка находится в очереди, ожидает обслуживания;
- в системе обслуживается одна заявка, и одна заявка находится в очереди, ожидает обслуживания;
…
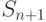 - в системе обслуживается одна заявка и
- в системе обслуживается одна заявка и  заявок находятся в очереди, ожидают обслуживания.
заявок находятся в очереди, ожидают обслуживания.
Граф состояний такой системы представляет схему "гибели и размножения" (рис. 2.12).
2.5.4. Одноканальная замкнутая СМО
Опишем состояния одноканальной замкнутой СМО.
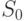 - заявок на обслуживание нет.
- заявок на обслуживание нет.
 - на обслуживании находится
- на обслуживании находится  заявок;
заявок;
 - общее число заявок, циркулирующих в системе;
- общее число заявок, циркулирующих в системе;
 - интенсивность требований на обслуживание от одной заявки.
- интенсивность требований на обслуживание от одной заявки.
Граф состояний одноканальной замкнутой СМО приведен на рис. 2.13. Модель данной СМО также представляет "схему гибели и размножения".
Однако не менее часто модель СМО не сводится к схеме "гибели и размножения". Например, в СМО с конечной надежностью каналов обслуживания.