Рисование графических примитивов средствами GDI+
Упражнение 11. Рисование дуг
Дуга - это сегмент эллипса. Чтобы определить дугу, нужно задать координаты эллипса, плюс угол для начальной и угловую длину дуги. Для рисования дуг используется четыре перегруженных метода DrawArc() класса Graphics
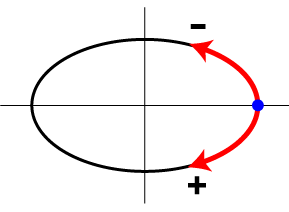
Два последних аргумента задают углы в градусах. Предпоследний аргумент определяет начало дуги, последний - угловую длину. Начало отсчета углов находится в точке пересечения горизонтальной линии, проходящей через центр эллипса, с правой половиной эллипса. Углы против часовой стрелки от точки отсчета считаются отрицательными, по часовой стрелке - положительными
Приведем код, рисующий эллипс с пунктирным контуром толщиной 30 пикселов. Угловой размер штрихов пунктира равен 10o, а промежутков между штрихами 15o - 10o = 5o
using System;
using System.Drawing;
using System.Windows.Forms;
namespace Test
{
public class DashedEllipse : PrintableForm
{
public DashedEllipse()
{
this.Text = "Рисование эллипса функцией DrawArc()";
}
// Перегруженная функция базового класса PrintableForm
protected override void DoPage(Graphics graphics, Color color, int cx, int cy)
{
int width = 30;
Rectangle rect = new Rectangle(width / 2, width / 2,
cx - 1 - width, cy - 1 - width);
Pen pen = new Pen(Color.Red, width);
for(int iAngle = 0; iAngle < 360; iAngle += 15)
graphics.DrawArc(pen, rect, iAngle, 10);
}
}
}
Листинг
16.20.
Рисование эллипса штрихом с помощью функции DrawArc() (DashedEllipse.cs)
Выходной экран имеет вид
Упражнение 12. Рисование прямоугольника с закругленными углами
В Win32 API есть функция RoundRect(), рисующая прямоугольник с закругленными углами. Эта функция принимает 4 аргумента, указывающих координаты левого верхнего и правого нижнего углов прямоугольника, плюс еще два, определяющие ширину и высоту эллипса, используемого для скругления углов прямоугольника. В классе Graphics BCL такой функции нет, но ее можно вполне имитировать, используя другие функции, вот каким кодом
using System;
using System.Drawing;
using System.Windows.Forms;
namespace Test
{
public class RoundRect : PrintableForm
{
public RoundRect()
{
this.Text = "Рисование прямоугольника со скругленными углами (RoundRect)";
}
// Перегруженная функция базового класса PrintableForm
protected override void DoPage(Graphics graphics, Color color, int cx, int cy)
{
RoundedRectangle(graphics, Pens.Red,
new Rectangle(0, 0, cx - 1, cy - 1),
new Size(cx / 5, cy / 5));
}
private void RoundedRectangle(Graphics gr, Pen pn, Rectangle rect, Size sz)
{
gr.DrawLine(pn, rect.Left + sz.Width / 2, rect.Top,
rect.Right - sz.Width / 2, rect.Top);
gr.DrawArc(pn, rect.Right - sz.Width, rect.Top,
sz.Width, sz.Height, 270, 90);
gr.DrawLine(pn, rect.Right, rect.Top + sz.Height / 2,
rect.Right, rect.Bottom - sz.Height / 2);
gr.DrawArc(pn, rect.Right - sz.Width, rect.Bottom - sz.Height,
sz.Width, sz.Height, 0, 90);
gr.DrawLine(pn, rect.Right - sz.Width / 2, rect.Bottom,
rect.Left + sz.Width / 2, rect.Bottom);
gr.DrawArc(pn, rect.Left, rect.Bottom - sz.Height,
sz.Width, sz.Height, 90, 90);
gr.DrawLine(pn, rect.Left, rect.Bottom - sz.Height / 2,
rect.Left, rect.Top + sz.Height / 2);
gr.DrawArc(pn, rect.Left, rect.Top,
sz.Width, sz.Height, 180, 90);
}
}
}
Листинг
16.21.
Рисование прямоугольника со скругленными углами (RoundRect.cs)
Нарисованная фигура состоит из восьми частей, нарисованных отдельно. Это значит, у каждой из восьми частей контура фигуры будут прорисованы концы, а соединения между ними нет, поэтому для толстых линий не будет согласованности в местах сочленения. Правильный путь объединения прямых и кривых в цельную фигуру состоит в использовании графического контура. Как это делается, будет показано в главе 15.