|
Не очень понятно про оболочечные Данные,ячейки памяти могут наверно размер менять,какое это значение те же операции только ячейки больше,по скорости тоже самое |
Работа с числами в языке Java
Данная часть посвящена изучению работы с числами на более глубоком уровне. В ней рассматривается машинное представление целых и вещественных чисел, эффективное для аппаратной реализации, а также объясняются особенности и проблемы, к которым приводит такое представление.
4.1. Двоичное представление целых чисел
Позиционные и непозиционные системы счисления
Позиционная система счисления - это такой способ записи числа, при котором вес цифры зависит от занимаемой позиции и пропорционален степени некоторого числа. Основание степени называется основанием системы счисления.
Например, число 2006 в десятичной системе счисления представляется в виде суммы тысяч, сотен, десятков и единиц:

то есть слагаемых с различными степенями числа 10. По основанию степени - числу десять - система называется десятичной. Другие позиционные системы счисления отличаются только числом в основании степени.
При написании программ чаще всего используют десятичную, шестнадцатеричную (основание шестнадцать), восьмеричную (основание восемь) и двоичную (основание два) системы. Число различных знаков - цифр, используемых для записи чисел - в каждой системе равно основанию данной системы счисления.
| 0,1 | - цифры двоичной системы |
| 0,1,2,3,4,5,6,7 | - цифры восьмеричной системы |
| 0,1,2,3,4,5,6,7,8,9 | - цифры десятичной системы |
| 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F | - цифры шестнадцатеричной системы |
В шестнадцатеричной системе "обычных" десятичных цифр недостаточно, и для обозначения цифр, больших девяти, используются заглавные латинские буквы A,B,C,D,E,F.
В дальнейшем везде, где это необходимо, мы будем указывать основание системы счисления индексом рядом с числом:  - в десятичной системе,
- в десятичной системе, 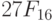 - в шестнадцатеричной системе,
- в шестнадцатеричной системе,  - в восьмеричной системе,
- в восьмеричной системе,  - в двоичной системе.
- в двоичной системе.
Существует множество непозиционных систем счисления, в которых числа изображаются и называются по своим правилам. Для римской системы чисел характерны сопоставление отдельного знака каждому большому числу ( V - пять, X - десять, L - пятьдесят, C - сто, M - тысяча ), повторение знака столько раз, сколько таких чисел во всем числе ( III - три, XX - двадцать), отдельные правила для предшествующих и последующих чисел (IV - четыре, VI - шесть, IX - девять). Множество непозиционных систем счисления связано с традиционными способами измерения конкретных величин - времени ( секунда, минута, час, сутки, неделя, месяц, год), длины ( дюйм, фут, ярд, миля, аршин, сажень), массы ( унция, фунт), денежных единиц. Выполнение арифметических действий в таких системах представляет собой крайне сложную задачу.
Приведем пример самой простой из возможных систем счисления – унарную. В ней имеется всего одна цифра 1. В унарной системе счисления число 1 изображается как 1, число 2 изображается как 11, число 3 как 111, число 4 как 1111, и так далее. Первоначально вместо единицы использовались палочки (помните детский сад?), поэтому такая система счисления иногда называется палочковой. Как ни странно, она является позиционной.
Позиционные системы счисления с основанием 2 и более удобны для алгоритмизации математических операций с числами (вспомните способ сложения и умножения "столбиком"). Двоичная система является естественным способом кодирования информации в компьютере, когда сообщение представляется набором нулей ("0" - нет сигнала на линии) и единиц ("1" - есть сигнал на линии). Для обозначения двоичных цифр применяется термин "бит", являющийся сокращением английского словосочетания "двоичная цифра" (BInary digiT).
Архитектура компьютера накладывает существенное ограничение на длину информации, обрабатываемой за одну операцию. Эта длина измеряется количеством двоичных разрядов и называется разрядностью. С помощью восьми двоичных разрядов можно представить  целых чисел. Порция информации размером 8 бит (8-ми битовое число) служит основной единицей измерения компьютерной информации и называется байтом (byte). Как правило, передача информации внутри компьютера и между компьютерами идет порциями, кратными целому числу байт.
целых чисел. Порция информации размером 8 бит (8-ми битовое число) служит основной единицей измерения компьютерной информации и называется байтом (byte). Как правило, передача информации внутри компьютера и между компьютерами идет порциями, кратными целому числу байт.
Машинным словом называют порцию данных, которую процессор компьютера может обработать за одну операцию (микрокоманду). Первые персональные компьютеры были 16-разрядными, т.е. работали с 16-битными (двухбайтными) словами. Поэтому операционные системы для этих компьютеров также были 16-разрядными. Например, MS DOS. Операционные системы для персональных компьютеров следующих поколений были 32-разрядны (Windows® '95/'98/NT/ME/2000/XP, Linux, MacOS®), так как предназначались для использования с 32-разрядными процессорами. Современные операционные системы либо 32-разрядны, либо даже 64-разрядны (версии для 64-разрядных процессоров).
Представление чисел в двоичной и шестнадцатеричной системах счисления, а также преобразование из одной системы в другую часто необходимо при программировании аппаратуры для измерений, контроля и управления с помощью портов ввода-вывода, цифро-аналоговых и аналого-цифровых преобразователей.
Двоичное представление положительных целых чисел
Целые числа в компьютере обычно кодируются в двоичном коде, то есть в двоичной системе счисления. Например, число 5 можно представить в виде  .
.
Показатель системы счисления принято записывать справа снизу около числа.
Аналогично, 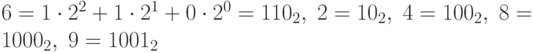 , и так далее. Все очень похоже на обозначение чисел в десятичной системе счисления:
, и так далее. Все очень похоже на обозначение чисел в десятичной системе счисления:
 . Но только в качестве основания системы счисления используется число
. Но только в качестве основания системы счисления используется число 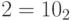 . У чисел, записанных в десятичной системе счисления, индекс 10 обычно не пишется, но его можно писать. Так что
. У чисел, записанных в десятичной системе счисления, индекс 10 обычно не пишется, но его можно писать. Так что 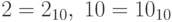 , и так далее.
, и так далее.
В двоичной арифметике всего две цифры, 0 и 1. Двоичный код положительного целого числа – это коэффициенты разложения числа по степеням двойки.
Умножение числа на двоичное десять, то есть на  , приводит к дописыванию справа нуля в двоичном представлении числа. Умножение на двоичное сто, то есть на
, приводит к дописыванию справа нуля в двоичном представлении числа. Умножение на двоичное сто, то есть на 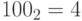 - дописыванию двух нулей. И так далее.
- дописыванию двух нулей. И так далее.
Целочисленное деление на 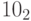 с отбрасыванием остатка производится путем отбрасывания последнего (младшего) бита, деление на
с отбрасыванием остатка производится путем отбрасывания последнего (младшего) бита, деление на  - отбрасывания двух последних бит, и так далее. Обычно такие операции называют побитовыми сдвигами на n бит влево (умножение на
- отбрасывания двух последних бит, и так далее. Обычно такие операции называют побитовыми сдвигами на n бит влево (умножение на  ) или вправо (целочисленное деление на
) или вправо (целочисленное деление на  ).
).
Сложение двоичных чисел можно производить "в столбик" по полной аналогии со сложением десятичных чисел. Единственное отличие – то, что в двоичной арифметике только две цифры, 0 и 1, а не десять цифр (от 0 до 9) как в десятичной. Поэтому если в десятичной арифметике единицу более старшего разряда дает, к примеру, сложение 1 и 9, то в двоичной арифметике ее даст сложение 1 и 1. То есть
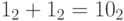
(в десятичной системе это равенство выглядит как 1+1=2). Аналогично, 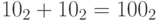 , и так далее.
, и так далее.
Примеры сложения "в столбик":
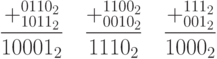
Совершенно аналогично выполняется умножение:
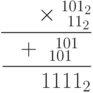
В машинной реализации целочисленного умножения используют побитовые сдвиги влево и сложения. Поскольку эти алгоритмы очень просты, они реализуются аппаратно.
