|
Не очень понятно про оболочечные Данные,ячейки памяти могут наверно размер менять,какое это значение те же операции только ячейки больше,по скорости тоже самое |
Работа с числами в языке Java
4.3. Двоичное представление вещественных чисел
Двоичные дроби
Целое число  можно представить в виде
можно представить в виде 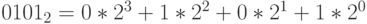
Аналогично можно записать двоичную дробь:

Заметим, что сдвиг двоичной точки на n разрядов вправо (чаще говорят о сдвиге самого числа влево) эквивалентен умножению числа на 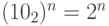 . Сдвиг точки влево (то есть сдвиг самого числа вправо) – делению на
. Сдвиг точки влево (то есть сдвиг самого числа вправо) – делению на  .
.
Мантисса и порядок числа
Рассмотрим сначала упрощенную схему хранения чисел в формате с плавающей точкой (floating point), несколько отличающуюся от реальной.
Число  с плавающей точкой может быть представлено в виде
с плавающей точкой может быть представлено в виде  . Множитель s – знак числа. Второй множитель m называется мантиссой, а число
. Множитель s – знак числа. Второй множитель m называется мантиссой, а число  – порядком числа.
– порядком числа.
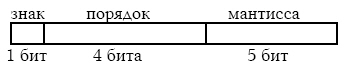
Для простоты рассмотрим 10-битовую ячейку, состоящую из трех независимых частей:
Первым идет знаковый бит. Если он равен 0, число положительно, если равен 1 – отрицательно. Набор бит, хранящийся в мантиссе, задает положительное число m, лежащее в пределах  . Оно получается из нашего двоичного числа путем переноса двоичной точки на место после первой значащей цифры числа. Например, числа
. Оно получается из нашего двоичного числа путем переноса двоичной точки на место после первой значащей цифры числа. Например, числа  ,
,  и
и  и имеют одну и ту же мантиссу, равную
и имеют одну и ту же мантиссу, равную  . При этом следующая за ведущей единицей точка в ячейке, выделяемой под мантиссу, не хранится - она подразумевается. То есть мантиссы приведенных чисел будут храниться в виде
. При этом следующая за ведущей единицей точка в ячейке, выделяемой под мантиссу, не хранится - она подразумевается. То есть мантиссы приведенных чисел будут храниться в виде  .
.
Число сдвигов двоичной точки (с учетом знака) хранится в части ячейки, выделяемой под порядок числа. В нашем примере числа  ,
,  и
и  будут иметь порядки 0, 1 и -1, соответственно. При перемножении чисел их мантиссы перемножаются, а порядки складываются. При делении – мантиссы делятся, а порядки вычитаются. И умножение, и деление мантисс происходит по тем же алгоритмам, что и для целых чисел. Но при выходе за размеры ячейки отбрасываются не старшие, а младшие биты. В результате каждая операция умножения или деления дает результат, отличающийся от точного на несколько значений младшего бита мантиссы. Аналогичная ситуация с потерей младших бит возникает при умножениях и делениях. Ведь если в ячейках для чисел данного типа хранится
будут иметь порядки 0, 1 и -1, соответственно. При перемножении чисел их мантиссы перемножаются, а порядки складываются. При делении – мантиссы делятся, а порядки вычитаются. И умножение, и деление мантисс происходит по тем же алгоритмам, что и для целых чисел. Но при выходе за размеры ячейки отбрасываются не старшие, а младшие биты. В результате каждая операция умножения или деления дает результат, отличающийся от точного на несколько значений младшего бита мантиссы. Аналогичная ситуация с потерей младших бит возникает при умножениях и делениях. Ведь если в ячейках для чисел данного типа хранится  значащих цифр числа, то при умножении двух чисел точный результат будет иметь
значащих цифр числа, то при умножении двух чисел точный результат будет иметь 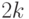 значащих цифр, последние
значащих цифр, последние  из которых
при записи результата в ячейку будут отброшены даже в том случае, если они сохранялись при вычислениях. А при делении в общем случае при точных вычислениях должна получаться бесконечная периодическая двоичная дробь, так что даже теоретически невозможно провести эти вычисления без округлений. С этим связана конечная точность вычислений на компьютерах при использовании формата с "плавающей точкой". При этом чем больше двоичных разрядов выделяется под мантиссу числа, тем меньше погрешность в такого рода операциях.
из которых
при записи результата в ячейку будут отброшены даже в том случае, если они сохранялись при вычислениях. А при делении в общем случае при точных вычислениях должна получаться бесконечная периодическая двоичная дробь, так что даже теоретически невозможно провести эти вычисления без округлений. С этим связана конечная точность вычислений на компьютерах при использовании формата с "плавающей точкой". При этом чем больше двоичных разрядов выделяется под мантиссу числа, тем меньше погрешность в такого рода операциях.
Замечание: системы символьных вычислений (или, что то же, – аналитических вычислений, или, что то же, системы компьютерной алгебры) позволяют проводить точные численные расчеты с получением результатов в виде формул. Однако они выполняют вычисления на много порядков медленнее, требуют намного больше ресурсов и не могут работать без громоздкой среды разработки. Поэтому для решения большинства практически важных задач они либо неприменимы, либо их использование нецелесообразно.
При сложении или вычитании сначала происходит приведение чисел к одному порядку: мантисса числа с меньшим порядком делится на  , а порядок увеличивается на
, а порядок увеличивается на  , где
, где  – разница в порядке чисел. При этом деление на
– разница в порядке чисел. При этом деление на  осуществляется путем сдвига мантиссы на
осуществляется путем сдвига мантиссы на  бит вправо, с заполнением освобождающихся слева бит нулями. Младшие биты мантиссы, выходящие за пределы отведенной под нее части ячейки, теряются.
бит вправо, с заполнением освобождающихся слева бит нулями. Младшие биты мантиссы, выходящие за пределы отведенной под нее части ячейки, теряются.
Пример:
сложим числа 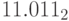 и
и 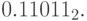 Для первого числа мантисса
Для первого числа мантисса  , порядок 1, так как
, порядок 1, так как  . Для второго – мантисса
. Для второго – мантисса  порядок -1, так как
порядок -1, так как  . Приводим порядок второго числа к значению 1, сдвигая мантиссу на 2 места вправо, так как разница порядков равна 2:
. Приводим порядок второго числа к значению 1, сдвигая мантиссу на 2 места вправо, так как разница порядков равна 2:

Но при таком сдвиге теряется два последних значащих бита мантиссы (напомним, хранится 5 бит), поэтому получаем приближенное значение  . Из-за чего в машинной арифметике получается
. Из-за чего в машинной арифметике получается

вместо точного значения 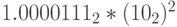 .
.
Таким образом, числа в описанном формате являются на деле рациональными, а не вещественными. При этом операции сложения, вычитания, умножения и деления выполняются с погрешностями, тем меньшими, чем больше разрядность мантиссы. Число двоичных разрядов, отводимых под порядок числа, влияет лишь на допустимый диапазон значений чисел, и не влияет на точность вычислений.
Научная нотация записи вещественных чисел
При записи программы в текстовом файле или выдачи результатов в виде "плоского текста" (plain text) невозможна запись выражений типа  . В этом случае используется так называемая научная нотация, когда вместо основания 10 пишется латинская буква E (сокращение от Exponent – экспонента). Таким образом,
. В этом случае используется так называемая научная нотация, когда вместо основания 10 пишется латинская буква E (сокращение от Exponent – экспонента). Таким образом,  запишется как 1.5E14, а
запишется как 1.5E14, а  как 0.31E-7. Первоначально буква E писалась заглавной, что не вызывало проблем. Однако с появлением возможности набора текста программы в нижнем регистре стали использовать строчную букву e, которая в математике используется для обозначения основания натуральных логарифмов. Запись вида
как 0.31E-7. Первоначально буква E писалась заглавной, что не вызывало проблем. Однако с появлением возможности набора текста программы в нижнем регистре стали использовать строчную букву e, которая в математике используется для обозначения основания натуральных логарифмов. Запись вида 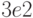 легко воспринять как
легко воспринять как 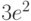 , а не
, а не 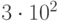 . Поэтому лучше использовать заглавную букву.
. Поэтому лучше использовать заглавную букву.
Литерные константы для вещественных типов по умолчанию имеют тип double. Например, 1.5 , -17E2 , 0.0 . Если требуется ввести литерную константу типа float, после записи числа добавляют постфикс f (сокращение от "float"): 1.5f , -17E2f , 0.0f .
Минимальное по модулю не равное нулю и максимальное значение типа float можно получить с помощью констант
-
Float.MIN_VALUE - равна

-
Float.MAX_VALUE - равна

Аналогичные значения для типа double - с помощью констант
-
Double.MIN_VALUE - равна

-
Double.MAX_VALUE - равна
 .
.
Стандарт IEEE 754 представления чисел в формате с плавающей точкой*
*Этот параграф является необязательным и приводится в справочных целях
В каком виде на самом деле хранятся числа в формате с плавающей точкой? Ответ дает стандарт IEEE 754 (другой вариант названия IEC 60559:1989), разработанный для электронных счетных устройств. В этом стандарте предусмотрены три типа чисел в формате с плавающей точкой, с которыми могут работать процессоры: real*4, real*8 и real*10. Эти числа занимают 4, 8 и 10 байт, соответственно. В Java типу real*4 соответствует float, а типу real*8 соответствует double. Тип real*10 из распространенных языков программирования используется только в диалектах языка PASCAL, в Java он не применяется.
Число  представляется в виде произведения знака
представляется в виде произведения знака  , мантиссы
, мантиссы  и экспоненты
и экспоненты 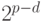 :
:

Число  называется порядком. Оно может меняться для разных чисел. Значение
называется порядком. Оно может меняться для разных чисел. Значение  , называемое сдвигом порядка, постоянное для всех чисел заданного типа. Оно примерно равно половине максимального числа
, называемое сдвигом порядка, постоянное для всех чисел заданного типа. Оно примерно равно половине максимального числа  , которое можно закодировать битами порядка. Точнее,
, которое можно закодировать битами порядка. Точнее, 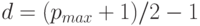 .
.
- Для чисел real*4:
 , d= 127.
, d= 127. - Для чисел real*8:
 , d= 1023.
, d= 1023. - Для чисел real*10:
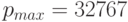 , d=16383.
, d=16383.
Число называется нормализованным в случае, когда мантисса лежит в пределах  . В этом случае первый бит числа всегда равен единице. Максимальное значение мантиссы достигается в случае, когда все ее биты равны 1. Оно меньше 2 на единицу младшего разряда мантиссы, то есть с практически важной точностью может считаться равным 2.
. В этом случае первый бит числа всегда равен единице. Максимальное значение мантиссы достигается в случае, когда все ее биты равны 1. Оно меньше 2 на единицу младшего разряда мантиссы, то есть с практически важной точностью может считаться равным 2.
Согласно стандарту IEEE 754 все числа формата с плавающей точкой при значениях порядка в диапазоне от 1 до  хранятся в нормализованном виде. Такое представление чисел будем называть базовым. Когда порядок равен 0, применяется несколько другой формат хранения чисел. Будем называть его особым. Порядок
хранятся в нормализованном виде. Такое представление чисел будем называть базовым. Когда порядок равен 0, применяется несколько другой формат хранения чисел. Будем называть его особым. Порядок  резервируется для кодировки нечисловых значений, соответствующее представление будем называть нечисловым. Об особом и нечисловом представлениях чисел будет сказано чуть позже.
резервируется для кодировки нечисловых значений, соответствующее представление будем называть нечисловым. Об особом и нечисловом представлениях чисел будет сказано чуть позже.
Размещение чисел в ячейках памяти такое:
| Тип | Байт1 | Байт2 | Байт3 | Байт4 | … | Байт8 | Байт9 | Байт10 |
|---|---|---|---|---|---|---|---|---|
| real*4 | sppp pppp | pmmm mmmm | mmmm mmmm | mmmm mmmm | ||||
| real*8 | sppp pppp | pppp mmmm | mmmm mmmm | mmmm mmmm | mmmm mmmm | |||
| real*10 | sppp pppp | pppp pppp | 1mmm mmmm | mmmm mmmm | mmmm mmmm | mmmm mmmm | mmmm mmmm |
Буква s обозначает знаковый бит; p – биты двоичного представления порядка, m – биты двоичного представления мантиссы. Если знаковый бит равен нулю, число положительное, если равен единице – отрицательное. В числах real*4 ( float ) и real*8 ( double ) при базовом представлении ведущая единица мантиссы подразумевается, но не хранится, поэтому реально можно считать, что у них под мантиссу отведено не 23 и 52 бита, которые реально хранятся, а 24 и 53 бита. В числах real*10 ведущая единица мантиссы реально хранятся, и мантисса занимает 64 бит. Под порядок в числах real*4 отведено 8 бит, в числах real*8 отведено 11 бит, а в числах real*10 отведено 15 бит.
Чему равны минимальное и максимальное по модулю числа при их базовом представлении?
Минимальное значение достигается при минимальном порядке и всех нулевых битах мантиссы (за исключением ведущего), то есть при m=1 и p=1. Значит, минимальное значение равно 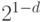 .
.
Максимальное значение достигается при максимальном порядке и всех единичных битах мантиссы, то есть при  и
и  . Значит, максимальное значение примерно равно
. Значит, максимальное значение примерно равно 
При значениях порядка в диапазоне от 1 до  базовое представление позволяет закодировать
базовое представление позволяет закодировать
- числа real*4 примерно от 2.350989E-38 до 3.402824E38,
- числа real*8 примерно от 2.225074E-308 до 1.797693E308,
- числа real*10 примерно от 3.362103E-4932 до 1.189731E4932.
В случае, когда порядок равен 0 или  , используется особое представление чисел, несколько отличающееся от базового.
, используется особое представление чисел, несколько отличающееся от базового.
Если все биты порядка равны 0, но мантисса отлична от нуля, то порядок считается равным 1 (а не 0), а вместо единицы в качестве подразумеваемой ведущей цифры используется ноль. Это ненормализованное представление чисел. Максимальное значение мантиссы в этом случае на младший бит мантиссы меньше 1. Так что максимальное значение числа в особой форме представления равно 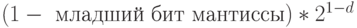 . То есть верхний предел диапазон изменения чисел в этом представлении смыкается с нижним диапазоном изменения чисел в базовом представлении.
. То есть верхний предел диапазон изменения чисел в этом представлении смыкается с нижним диапазоном изменения чисел в базовом представлении.
Минимальное ненулевое значение мантиссы в особом представлении равно 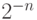 , где n – число бит мантиссы после двоичной точки.
, где n – число бит мантиссы после двоичной точки.
Минимальное отличное от нуля положительное число для некоторого типа чисел с плавающей точкой равно 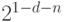 .
.
Таким образом, особое представление позволяет закодировать
- числа real*4 примерно от 1.401298E-45 до 2.350989E-38,
- числа real*8 примерно от 4.940656E-324 до 2.225074E-308,
- числа real*10 примерно от 3.6451995E-4951 до 3.362103E-4932.
Специальный случай особого представления – когда и порядок и мантисса равны нулю. Это значение обозначает машинный ноль. В соответствии со стандартом IEEE 754 имеются +0 и -0. Но во всех известных автору языках программирования +0 и -0 при вводе-выводе и сравнении чисел отождествляются.
Нечисловое представление соответствует случаю, когда 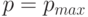 , то есть все биты порядка равны 1. Такое "число" в зависимости от значения мантиссы обозначает одно из трех специальных нечисловых значений, которые обозначают как Inf (Infinity - "бесконечность"), NaN (Not a Number - "не число"), Ind (Indeterminate – "неопределенность"). Эти значения появляются при переполнениях и неопределенностях в вычислениях. Например, при делении 1 на 0 получается Inf, а при делении 0 на 0 получается Ind. Значение NaN может получаться при преобразовании строки в число, взятии логарифма от отрицательного числа, тригонометрической функции от бесконечности и т.п.
, то есть все биты порядка равны 1. Такое "число" в зависимости от значения мантиссы обозначает одно из трех специальных нечисловых значений, которые обозначают как Inf (Infinity - "бесконечность"), NaN (Not a Number - "не число"), Ind (Indeterminate – "неопределенность"). Эти значения появляются при переполнениях и неопределенностях в вычислениях. Например, при делении 1 на 0 получается Inf, а при делении 0 на 0 получается Ind. Значение NaN может получаться при преобразовании строки в число, взятии логарифма от отрицательного числа, тригонометрической функции от бесконечности и т.п.
Значение Inf соответствует нулевым битам мантиссы.Согласно IEEE 754 бесконечность имеет знак. Если знаковый бит 0 это + Inf, если знаковый бит 1 это –Inf.
Значение Ind кодируется единицей в знаковом бите и битами мантиссы, равными 0 во всех разрядах кроме старшего (реального, а не подразумеваемого), где стоит 1. Все остальные сочетания знакового бита и мантиссы отведены под величины NaN. Значения NaN бывают двух типов – вызывающие возбуждение сигнала о переполнении ( Signaling NaN ) и не вызывающие ( Quiet NaN ). Значения обоих этих типов могут быть "положительными" (знаковый бит равен нулю) и "отрицательными" (знаковый бит равен единице).
В современных языках программирования поддерживается только часть возможностей, реализованных в процессорах в соответствии со стандартом IEEE 754. Например, в Java значения бесконечности различаются как по знаку, так и по типу: имеются
Float.NEGATIVE_INFINITY, Float.POSITIVE_INFINITY, Double.NEGATIVE_INFINITY, Double.POSITIVE_INFINITY.
Но значение Ind вообще не употребляется и отождествляется с NaN, хотя Float.NaN и Double.NaN различаются.
Числа в формате с плавающей точкой занимают следующие диапазоны значений:
Имеются методы оболочечных классов, позволяющие преобразовывать наборы бит, хранящихся в ячейках типа int, в значения float, и наоборот – значения типа float в их битовое представление типа int. При этом содержание ячеек не меняется – просто содержащиеся в ячейках наборы бит начинают по-другому трактоваться.
Аналогичные операции существуют и для значений типа long и double:
- Float.intBitsToFloat ( значение типа int )
- Double.longBitsToDouble ( значение типа long )
- Float.floatToIntBits ( значение типа float )
- Double.doubleToLongBits ( значение типа double )
Например,
- Float.intBitsToFloat(0x7F7FFFFF) даст значение, равное Float.MAX_VALUE,
- Float.intBitsToFloat(0x7F800000) – значение Float.POSITIVE_INFINITY,
- Float.intBitsToFloat(0xFF800000) – значение Float.NEGATIVE_INFINITY.
Если аргумент метода Float.intBitsToFloat лежит в пределах от 0xF800001 до 0xF800001, результатом будет Float.NaN.
Следует подчеркнуть, что данные операции принципиально отличаются от "обычных" преобразований типов, например, из int в float или из double в long. При "обычных" преобразованиях значение числа не меняется, просто меняется форма хранения этого значения и, соответственно, наборы битов, которыми кодируется это значение. Причем может измениться размер ячейки (скажем, при преобразовании значений int в значения double ). А при рассматриваемых в данном разделе операциях сохраняется набор бит и размер ячейки, но меняется тип, который приписывается этому набору.
Краткие итоги
- Отрицательные целые числа кодируются в дополнительном коде.
- При сложении, вычитании и, особенно, умножении целых чисел может возникать выход за пределы допустимого диапазона. В результате у результата может получиться значение, имеющее противоположный по сравнению с правильным результатом знак. Или нуль при сложении чисел одного знака.
- Побитовая маска AND (оператор "&" ) служит для сбрасывания в 0 тех битов числа, где в маске стоит 0, остальные биты числа не меняются. Побитовая маска OR (оператор "|" ) служит для установки в 1 тех битов числа, где в маске стоит 1, остальные биты числа не меняются.
- Побитовая маска XOR (оператор "^" ) служит для инверсии тех битов числа, где в маске стоит 1 (единицы переходят в нули, а нули – в единицы), остальные биты числа не меняются. Имеется команда перевода вывода графики в режим XOR при рисовании, для этого используется команда graphics.setXORMode(цвет).
- Инверсия всех битов числа осуществляется с помощью побитового отрицания ~a.
- Побитовые сдвиги "<<", ">>" и ">>>" приводят к перемещению всех бит ячейки, к которой применяется оператор, на указанное число бит влево или вправо. Причем m<<n является очень быстрым вариантом операции
 , а m>>n – целочисленному делению m на
, а m>>n – целочисленному делению m на  .
. - Литерные константы для вещественных типов по умолчанию имеют тип double. Например, 1.5 , -17E2 , 0.0 . Если требуется ввести литерную константу типа float, после записи числа добавляют постфикс f (сокращение от "float"): 1.5f , -17E2f , 0.0f .
- Число в формате с плавающей точкой состоит из знакового бита, мантиссы и порядка. Все операции с числами такого формата сопровождаются накоплением ошибки порядка нескольких младших битов мантиссы ненормализованного результата.
- При проведении умножения и деления чисел в формате с плавающей точкой не происходит катастрофической потери точности результата. А при сложениях и вычитаниях такая потеря может происходить в случае, когда вычисляется разность двух значений, к которым прибавляется малая относительно этих значений добавка. Число порядков при потере точности равно числу порядков, на которые отличаются эти значения от малой добавки.
Типичные ошибки:
- При использовании целых типов не знают или забывают, что при выходе за пределы диапазона соответствующие биты отбрасываются без всякой диагностики переполнения. И что получившийся результат может быть неправильного знака или нуль. Особенно часто переполнение возникает при умножении нескольких целых величин друг на друга.
- Написание численных алгоритмов с катастрофической потерей точности.
- Сравнение двух чисел в формате с плавающей точкой на равенство или неравенство в случае, когда в точной арифметике они должны быть равны.
Задания
- Создать проект с графическим пользовательским интерфейсом, в котором имеется два пункта ввода и радиогруппа с выбором варианта для каждого из целочисленных типов, а также кнопки JButton с надписями "Сложить" и "Умножить". При выборе соответствующего варианта в пунктах ввода должны возникать случайным образом генерируемые числа, лежащее в пределах допустимых значений для этого типа. При нажатии на кнопку содержимое пунктов ввода и результат действий должны быть преобразованы в значения соответствующего типа, и результат выполнения сложения или умножения должен быть показан в метке. Проверить наличие проблемы арифметического переполнения для разных значений каждого типа. Выяснить, в каком случае чаще происходит переполнение – при сложении или умножении. И насколько часто встречаются такие значения одного знака, чтобы в результате получился результат противоположного знака. Вручную ввести в пункты ввода такие значения одного знака, чтобы в результате получилось нулевое значение.
- Написать приложение с графическим пользовательским интерфейсом, в котором вычисляется выражение 1+x и присваиваются переменной float f, а также вычисляется выражение 1+y и присваиваются переменной double d. Величины x типа float и y типа double вводится пользователем с помощью пунктов ввода. Вывести в метку jLabel1 разность f-1, и в метку jLabel2 разность d-1. Провести вычисления для x и y, меняющихся в пределах от 1E-3 до 1E-18 . Объяснить результаты.
-
* Для студентов технических вузов и физико-математических факультетов университетов. Написать приложение с графическим пользовательским интерфейсом, в котором вычисляются выражения
 и
и  , где
, где 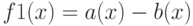 ,
,  ,
, 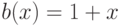 , и
, и 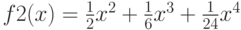 . Поскольку f2(x) состоит из первых членов разложения f1(x) в ряд, то f1(x) и f2(x) должны быть примерно равны . Требуется сравнить значения выражения f1(x) и f2(x) при различных x. Все вычисления сначала проводить для переменных и функций типа float, а затем - для переменных и функций типа double. Величина x вводится пользователем.
Вывести в метки значения f1_double (x), a_double(x), b_double(x), f1_float(x), a_float(x), b_float(x), а также разности f1_float(x)-f2_float(x) и f1_double (x) - f2_double (x). Провести такое сравнение для аргументов x, меняющихся в пределах от 1E-8 до 0.1. Объяснить результаты.
. Поскольку f2(x) состоит из первых членов разложения f1(x) в ряд, то f1(x) и f2(x) должны быть примерно равны . Требуется сравнить значения выражения f1(x) и f2(x) при различных x. Все вычисления сначала проводить для переменных и функций типа float, а затем - для переменных и функций типа double. Величина x вводится пользователем.
Вывести в метки значения f1_double (x), a_double(x), b_double(x), f1_float(x), a_float(x), b_float(x), а также разности f1_float(x)-f2_float(x) и f1_double (x) - f2_double (x). Провести такое сравнение для аргументов x, меняющихся в пределах от 1E-8 до 0.1. Объяснить результаты.