|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Многостанционный доступ с кодовым разделением и сети CDMA
3.1. Многостанционный доступ с кодовым разделением
Многостанционный доступ с кодовым разделением (CDMA — Code Division Multiple Access) — технология, отличающаяся от доступа с частотным разделением и доступа с временным разделением [45, 80, 105]. Она не использует для разделения каналов ни частоты, ни времени, хотя по многим признакам она напоминает частотный доступ ( рис. 3.1).
Каждый входной цифровой сигнал складывается ("модулируется") с отдельной "несущей", в качестве которой выступает псевдослучайная последовательность (ПСП). ПСП передается со скоростью большей, чем скорость исходного сигнала, после чего полученные сигналы объединяются в единый поток. При этом полоса частот, используемая в радиоканале, гораздо шире, чем полоса исходного сигнала. Этот процесс получил название расширение спектра (Spreading Specter) [119]. Псевдослучайные последовательности выбираются таким образом, чтобы на приемном конце их можно было разделить (отфильтровать) и отделить сигнал от его псевдослучайной последовательности ("несущей"). Передача единого объединенного потока осуществляется в одной полосе частот с помощью одного из видов фазовой манипуляции. Поэтому системы, основанные на CDMA, не требуют разделения полосы частот на отдельные каналы, что, в свою очередь, облегчает процесс хэндовера (переход из одной соты в другую).
Псевдослучайные последовательности должны иметь нулевую корреляцию, т. е. быть взаимонезависимы.
Существует два способа множественного (многостанционного) доступа с кодовым разделением каналов (CDMA):
- ортогональный многостанционный доступ;
- неортогональный многостанционный доступ, или асинхронный многостанционный доступ с кодовым разделением каналов.
3.1.1. Функции Уолша
Для первого способа разделения применяются ортогональные функции Уолша [119, 120] и функции, получаемые на их базе. Это набор ортогональных последовательностей длиной  , в которых используются только два значения: +1 и –1.
, в которых используются только два значения: +1 и –1.
Функции являются цифровыми "аналогами синусоид". При кодировании обычно символ +1 заменяется на 0, а –1 на 1.
Рассмотрим систему двоичных чисел от 0 до 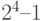 (числа от 0 до 15), которые приведены в табл. 3.1.
(числа от 0 до 15), которые приведены в табл. 3.1.
Она представляет собой функцию, содержащую четыре переменных ( 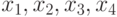 ).
).
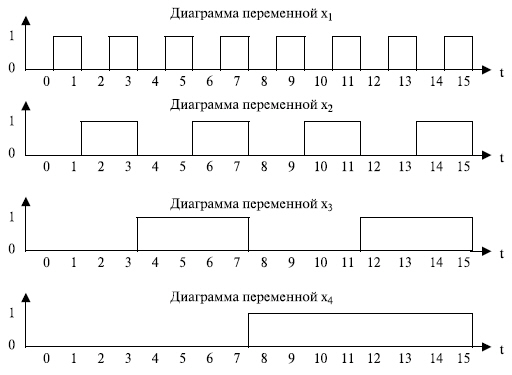
Если предположить, что каждый разряд этих чисел поступает согласно десятичному номеру в таблице, то это можно изобразить следующими диаграммами ( рис. 3.2), которые представляют периодические функции, подобные синусу (инверсные переменные подобны косинусу).
На основе этих функций могут быть получены любые другие функции Уолша на конечном отрезке от 0 до 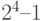 .
.
Вторая трактовка функций Уолша — это диаграмма коэффициентов при отображении двоичных чисел в двоичную систему.
| X4 | X3 | X2 | X1 | № |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 0 | 0 | 0 | 8 |
| 1 | 0 | 0 | 1 | 9 |
| 1 | 0 | 1 | 0 | 10 |
| 1 | 0 | 1 | 1 | 11 |
| 1 | 1 | 0 | 0 | 12 |
| 1 | 1 | 0 | 1 | 13 |
| 1 | 1 | 1 | 0 | 14 |
| 1 | 1 | 1 | 1 | 15 |
Известно, что для перехода от двоичных чисел к их десятичным эквивалентам применяются весовые коэффициенты, сумма которых дает соответствующее число:
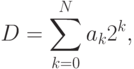
где  — число разрядов двоичного числа,
— число разрядов двоичного числа, 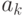 — значение k-го разряда двоичного числа.
— значение k-го разряда двоичного числа.
В этом случае каждая диаграмма на
рис.
3.2 указывает моменты появления чисел, в которые входит заданный числовой коэффициент. Например, весовой коэффициент 2 входит в числа 2, 3, 6, 7, 10, 11, 14, 15. Этот ряд чисел отображается периодической функцией Уолша, обозначенной на
рис.
3.2 как диаграмма переменной  .
.