|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Многостанционный доступ с кодовым разделением и сети CDMA
3.1.2. Корреляция и ортогональные функции Уолша
Как было сказано выше, для объединения нескольких каналов при кодовом разделении каналов необходимо, чтобы псевдослучайные коды были разделимы с помощью корреляционного фильтра. Для этого они должны достаточно различаться. Степень подобия (похожести) функций в математике отображается с помощью корреляции. Различаются взаимная корреляция — сравнение двух функций, ортогональная корреляция — при полной независимости двух функций и автокорреляция — сравнение функции с собой при сдвиге во времени.
- Взаимная корреляция (cross correlation) для двух периодических функций с периодом
 определяется формулой:Она измеряет подобие двух сигналов, сдвинутых во времени.
определяется формулой:Она измеряет подобие двух сигналов, сдвинутых во времени.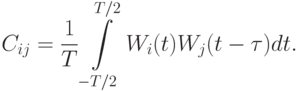
- Ортогональная корреляция — это частный случай взаимной корреляции, когда эта функция равна нулю:Эти сигналы могут передаваться одновременно, поскольку они не создают взаимных помех.
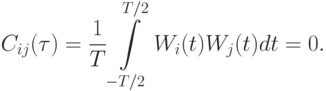
- Автокорреляция периодического сигнала определяется следующей формулой:Она определяет подобие данной функции с ее же версией, сдвинутой во времени.
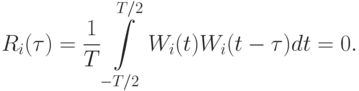
Для дискретных функций интегрирование можно заменить суммированием.
В системах многостанционного доступа с кодовым разделением каналов применяются ортогональные функции Уолша. Одним из необходимых (но не достаточных) свойств такого кода является его сбалансированность, т. е. одинаковое число нулей и единиц.
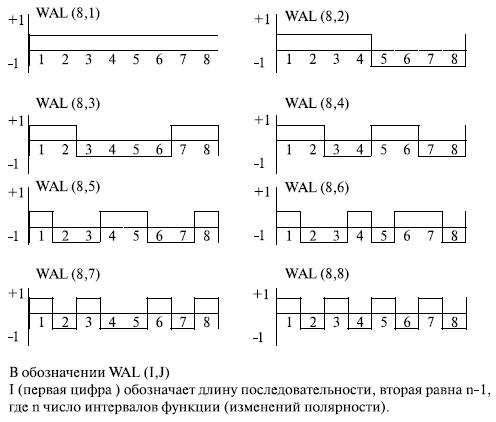
Ниже (табл. 3.2) показаны ортогональные функции Уолша длины  [3, 22, 101, 120, 121].
[3, 22, 101, 120, 121].
Заметим, что при кодировании обычно символ 0 заменяется на +1, а 1 на –1.
| WAL(8,1)=0000 0000 |
| WAL(8,2)=0000 1111 |
| WAL(8,3)=0011 1100 |
| WAL(8,4)=0011 0011 |
| WAL(8,5)=0110 0110 |
| WAL(8,6)=0110 1001 |
| WAL(8,7)=0101 1010 |
| WAL(8,8)=1010 1010 |
На рис. 3.3 приведены диаграммы, соответствующие этим последовательностям.
Ортогональные функции Уолша могут быть сгенерированы с использованием итерационного процесса построения матрицы Адамара [22] начиная с ![H_1=[0]](/sites/default/files/tex_cache/a8eda5a09c6c26ae92b3ffa89b6dc8fb.png) . Матрица Адамара сформирована:
. Матрица Адамара сформирована:

Коды Уолша—Адамара длины 2 и 4 будут получены соответственно:

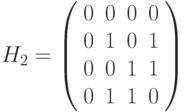
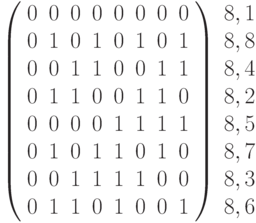
Полученная матрица с точностью до порядка следования совпадает с ортогональными функциями, приведенными в табл. 3.2. Для того чтобы облегчить сравнение, справа от матрицы приведены номера функций по табл. 3.2 и диаграмме рис. 3.3.
Рассмотрим пример вычисления ортогональности полученных функций. Разберем взаимную корреляцию (без сдвига) функций 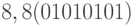 и
и  .
.
![\begin{array}{l}[(-1)\times(-1)]+[(1\times1)]+[(-1)\times1]+[1\times(-1)]+[(-1)\times1]+[1\times(-1)]+[(-1)(-1)]+[1\times1]=0 \atop {1\qquad\qquad 2\qquad\quad 3\qquad\quad 4\qquad\qquad 5\qquad\quad 6\qquad\qquad 7\qquad\qquad 8\qquad\quad\end{array}](/sites/default/files/tex_cache/6061d7de600d2487f240d3df01a2bc98.png)
Согласно полученному результату эти две функции ортогональны.
Однако ортогональные функции Уолша имеют недостатки. Система должна быть синхронизирована. При сдвиге синхронизации функции корреляция увеличивается.
Для сдвинутых по времени и несинхронизированных сигналов взаимная корреляция может быть не равна нулю. Они могут интерферировать друг с другом. Вот почему кодирование с помощью функций Уолша может применяться только при синхронном CDMA.
3.1.3. Неортогональные псевдослучайные функции
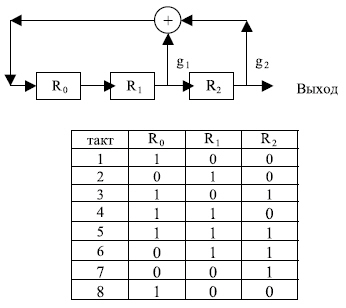
Неортогональные (асинхронные) псевдослучайные функции могут быть сгенерированы с применением сдвиговых регистров, сумматоров (сложение по модулю 2) и контуров обратной связи. Рис. 3.4 иллюстрирует такой принцип.
Максимальная длина последовательности определяется длиной регистра и конфигурацией цепи обратной связи (на
рис.
3.4 цепи обратной связи обозначены 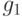 ,
,  ). Регистр длиной
). Регистр длиной  битов может порождать свыше
битов может порождать свыше 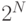 различных комбинаций нулей и единиц. Так как цепь обратной связи выполняет линейные операции, то если все регистры будут иметь нулевое значение, выход цепи обратной связи также будет нулевой. Поэтому, если установить все разряды на нуль, то цепь обратной связи будет всегда давать нулевой выход для всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. Таким образом, максимальная длина любой последовательности равна
различных комбинаций нулей и единиц. Так как цепь обратной связи выполняет линейные операции, то если все регистры будут иметь нулевое значение, выход цепи обратной связи также будет нулевой. Поэтому, если установить все разряды на нуль, то цепь обратной связи будет всегда давать нулевой выход для всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. Таким образом, максимальная длина любой последовательности равна 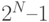 . Генерируемые последовательности называются последовательностями максимальной длины, или m-последовательностями.
Основное свойство таких последовательностей: автокорреляционная функция m-последовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случаях. Это позволяет более четко выделять каналы. Конфигурации обратной связи для m-последовательности сведены в таблицу и могут быть найдены в [61].
. Генерируемые последовательности называются последовательностями максимальной длины, или m-последовательностями.
Основное свойство таких последовательностей: автокорреляционная функция m-последовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случаях. Это позволяет более четко выделять каналы. Конфигурации обратной связи для m-последовательности сведены в таблицу и могут быть найдены в [61].
Последовательности, порождаемые регистрами сдвига, имеют еще много вариантов. В частности, известны последовательности Голда, порождаемые совокупностью двух регистров, последовательности Касами, порождаемые тремя регистрами, и т. д. [23, 61].