|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Принятие решений на основе моделей обеспечения качества
Оценка снизу необходимого объема выборки. Как известно, в теории статистического приемочного контроля качества продукции разработано много подходов к выбору планов контроля:
- на основе приемочного и браковочного уровней дефектности;
- исходя из предела среднего выходного уровня дефектности (при контроле с разбраковкой);
- с использованием экономических показателей, относящихся к предприятию (см., например, ГОСТ 24660-81);
- с использованием экономических показателей, относящихся к народному хозяйству в целом; и т.д.
Имеется обширная литература, посвященная обоснованию и сравнению этих подходов, разработке соответствующей математической теории и программного обеспечения. Не углубляясь в эти проблемы, сосредоточим внимание на одном парадоксальном явлении: при повышении качества выпускаемой продукции теория рекомендует увеличивать объем контроля!
Действительно, при повышении качества выпускаемой продукции требования потребителя, очевидно, обеспечиваются все лучше. Следовательно, должен уменьшаться браковочный уровень дефектности, т.е. то значение входного уровня дефектности, при котором вероятность приемки партии равна риску потребителя. Из всех планов с общим объемом контроля n минимум вероятности приемки партии (т.е. оперативной характеристики) достигается на одноступенчатом плане  . (Напомним, что согласно этому плану партия принимается тогда и только тогда, когда из n проверенных единиц продукции все оказываются годными.) Другими словами, оперативная характеристика для плана
. (Напомним, что согласно этому плану партия принимается тогда и только тогда, когда из n проверенных единиц продукции все оказываются годными.) Другими словами, оперативная характеристика для плана  является огибающей (снизу) множества всех оперативных характеристик. Следовательно, из всех планов с общим объемом контроля n минимум браковочного уровня дефектности достигается также на плане
является огибающей (снизу) множества всех оперативных характеристик. Следовательно, из всех планов с общим объемом контроля n минимум браковочного уровня дефектности достигается также на плане  .
.
В дальнейшем будем исходить из биномиальной модели выборки, согласно которой число дефектных единиц продукции в выборке объема n имеет биномиальное распределение с параметрами n и p, где p - входной уровень дефектности. Как хорошо известно, эта модель является приближением для модели простой случайной выборки из партии, согласно которой указанное число имеет гипергеометрическое распределение. Напомним, что по чисто математическим причинам гипергеометрическая модель переходит в биномиальную с параметрами 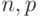 , когда объем партии
, когда объем партии  безгранично возрастает, а доля дефектных единиц продукции в партии приближается к p. Если объем выборки составляет не более 10% объема партии, то с достаточной для практики точностью принимают, что соответствующее биномиальное распределение хорошо приближает гипергеометрическое.
безгранично возрастает, а доля дефектных единиц продукции в партии приближается к p. Если объем выборки составляет не более 10% объема партии, то с достаточной для практики точностью принимают, что соответствующее биномиальное распределение хорошо приближает гипергеометрическое.
Примем обычное предположение о том, что риск потребителя равен 0,10. Как известно, браковочный уровень дефектности  для плана
для плана  определяется из условия
определяется из условия
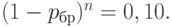
Это соотношение дает возможность по заданному браковочному уровню дефектности  найти необходимый объем выборки:
найти необходимый объем выборки:
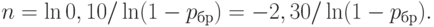
Поскольку в силу сказанного ранее представляют интерес малые значения браковочного уровня дефектности, воспользуемся тем, что при малых x согласно правилам математического анализа

Вторым слагаемым в правой части последней формулы, как обычно в асимптотических рассуждениях, можно пренебречь. Следовательно, необходимый объем выборки с достаточной точностью может быть найден по формуле
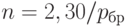 |
( 14) |
(При конкретных расчетах надо, очевидно, правую часть округлить до ближайшего целого числа.) Например, при довольно низком (с точки зрения мирового рынка) качестве выпускаемой продукции можно задать 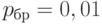 , т.е. потребовать, чтобы почти все (точнее, не менее 90%) партии, в которых дефектных единиц больше, чем 1 из 100, были забракованы и не достигли потребителя. Тогда объем контроля должен составлять не менее
, т.е. потребовать, чтобы почти все (точнее, не менее 90%) партии, в которых дефектных единиц больше, чем 1 из 100, были забракованы и не достигли потребителя. Тогда объем контроля должен составлять не менее  .
.
Основной парадокс теории статистического приемочного контроля. Как следует из сказанного выше, необходимый объем выборки, определяемый для какого-либо плана контроля по заданному браковочному уровню дефектности  , будет не меньше, чем для плана
, будет не меньше, чем для плана  , т.е. не меньше, чем
, т.е. не меньше, чем 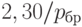 .Таким образом, если достигнут достаточно высокий уровень качества, такой, что потребителю может попасть не более 1 дефектной единицы продукции из 10000, т.е.
.Таким образом, если достигнут достаточно высокий уровень качества, такой, что потребителю может попасть не более 1 дефектной единицы продукции из 10000, т.е. 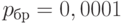 , то объем контроля должен быть не меньше
, то объем контроля должен быть не меньше  . Если же качество повысится в 100 раз, т.е. потребителю сможет попасть не более 1 дефектной единицы продукции из 1000000, то объем контроля и затраты на него возрастут также в 100 раз, и минимально необходимый объем контроля составит 2,3 миллиона единиц продукции. (Напомним, что в системе "Шесть сигм" ориентиром является уровень "3,4 дефекта на 1000000 возможностей"
[14.6].) Поскольку объем партий большинства (практически всех!) видов продукции существенно меньше этого числа, то проведенные выше расчеты говорят о необходимости перехода на сплошной контроль.
. Если же качество повысится в 100 раз, т.е. потребителю сможет попасть не более 1 дефектной единицы продукции из 1000000, то объем контроля и затраты на него возрастут также в 100 раз, и минимально необходимый объем контроля составит 2,3 миллиона единиц продукции. (Напомним, что в системе "Шесть сигм" ориентиром является уровень "3,4 дефекта на 1000000 возможностей"
[14.6].) Поскольку объем партий большинства (практически всех!) видов продукции существенно меньше этого числа, то проведенные выше расчеты говорят о необходимости перехода на сплошной контроль.
Итак, выводы парадоксальны: если качество выпускаемой продукции не очень хорошее, то целесообразно проводить статистический (выборочный) контроль, если же качество возрастает, то объем контроля и затраты на него увеличиваются, вплоть до перехода на сплошной контроль. Если это возможно, т.е. контроль не является разрушающим. А если невозможно, то попадаем в тупиковую ситуацию - высокое качество в принципе не может быть подтверждено результатами контроля.
В реальных ситуациях объемы контролируемых выборок - единицы или десятки, но обычно отнюдь не сотни и тысячи. Если контролируются 100 изделий, то согласно формуле (14) браковочный уровень дефектности равен 2,3%. И это - предел для реально используемых объемов контроля. Следовательно, статистический приемочный контроль (в том числе выходной или входной) может быть применен для контроля лишь такой продукции, в которой из 50 изделий хотя бы одно дефектно. Другими словами, этот метод управления качеством предназначен лишь для продукции сравнительно низкого качества (входной уровень дефектности не менее 1-2%) или при обслуживании потребителя, согласного на довольно высокий браковочный уровень дефектности (не менее 2,3%).
Следовательно, для повышения качества необходимо использовать контрольные карты и другие методы статистического регулирования технологических процессов на предприятии. О них рассказано ниже. В частности, упомянем методы "всеобщего" (в другом переводе - тотального) контроля качества [14.9] и др. Недаром этим методам уделяется больше внимания в зарубежных методических изданиях, чем собственно статистическому приемочному контролю.
От контроля к пополнению партии. Рассмотрим простую идею: отказываемся от контроля качества вообще, но зато по первому требованию потребителя заменяем дефектную единицу продукции на новую. При этом экономим на контроле, но вместо этого тратим средства на замену продукции. Выгодно это или не выгодно?
Замена продукции может проводиться различными способами. Для многих видов товаров народного потребления это делается с помощью системы гарантийного обслуживания, гарантийных сроков и мастерских, через сеть розничной торговли и т.д.
Другой вариант - к партии поставляемой продукции добавляется некоторое количество единиц продукции для замены имеющихся, возможно, в ней дефектных единиц. Сначала обсудим подробнее именно этот вариант идеи замены продукции.
Пусть поставщик выпускает продукцию с известным ему уровнем дефектности p. Тогда число Х дефектных единиц в партии объема  имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами  и p. По теореме Муавра-Лапласа
и p. По теореме Муавра-Лапласа  не превосходит (при достаточно большом
не превосходит (при достаточно большом  ) величины
) величины
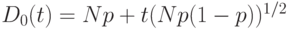
с вероятностью 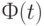 , где
, где 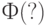 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Поскольку
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Поскольку 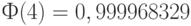 , то для практических целей достаточно положить
, то для практических целей достаточно положить 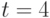 , при этом более чем
, при этом более чем 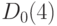 дефектных единиц продукции попадет в партию лишь в 3 случаях из 100000 (при более точном расчете необходимо учесть отличие биномиального распределения от нормального, например, использовать неравенство Берри-Эссеена).
дефектных единиц продукции попадет в партию лишь в 3 случаях из 100000 (при более точном расчете необходимо учесть отличие биномиального распределения от нормального, например, использовать неравенство Берри-Эссеена).
Пусть  - цена одной единицы продукции,
- цена одной единицы продукции,  - стоимость неразрушающего контроля одной единицы продукции (с исправлением дефектов при их обнаружении). Сравним сначала две стратегии технико-экономических отношений поставщика с потребителями:
- стоимость неразрушающего контроля одной единицы продукции (с исправлением дефектов при их обнаружении). Сравним сначала две стратегии технико-экономических отношений поставщика с потребителями:
и пополнение партии дополнительными изделиями в числе 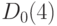 (затраты
(затраты 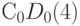 ).
).
Вторая стратегия лучше (экономически выгоднее), если
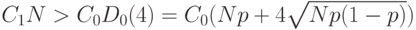 |
( 15) |
Поделим на 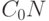 получим равносильное неравенство
получим равносильное неравенство
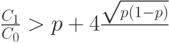
Поскольку 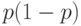 не превосходит 1/4 при всех
не превосходит 1/4 при всех 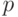 , то из неравенства
, то из неравенства
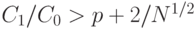 |
( 16) |
вытекает неравенство (15). Ясно, что в случае, если
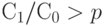
неравенство (16) (а потому и неравенство (15)) выполняется при достаточно больших объемах партии, а именно, при
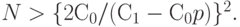
Например, если стоимость контроля составляет 10% от стоимости продукции (типовая ситуация в машиностроении), т.е. 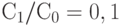 , а уровень дефектности
, а уровень дефектности 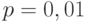 , то последнее неравенство дает
, то последнее неравенство дает 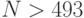 . В то же время нетрудно проверить, что неравенство (15) выполняется при
. В то же время нетрудно проверить, что неравенство (15) выполняется при
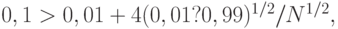
т.е. при  . Расхождение более чем на порядок (в 26 раз) объясняется заменой при переходе от формулы (15) к формуле (16) величины
. Расхождение более чем на порядок (в 26 раз) объясняется заменой при переходе от формулы (15) к формуле (16) величины 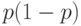 на 1/4, т.е. на гораздо большую величину - при малом входном уровне дефектности p.
на 1/4, т.е. на гораздо большую величину - при малом входном уровне дефектности p.
Выгодно ли введение статистического контроля? Пусть рассматривается описанная выше стратегия пополнения партий. Мы сравнивали ее со стратегией сплошного контроля, которая во многих случаях оказалась хуже. Может быть, поставщику имеет смысл использовать статистический контроль? Понятно, что речь может идти лишь о (неразрушающем) контроле с разбраковкой, поскольку только в этом случае меняется доля дефектности в потоке партий, направляемых потребителям.
Пусть используется план 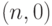 с приемочным уровнем дефектности, равным реально достигнутому предприятием уровню дефектности p. Как известно, тогда объем выборки определяется из условия
с приемочным уровнем дефектности, равным реально достигнутому предприятием уровню дефектности p. Как известно, тогда объем выборки определяется из условия
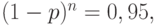
т.е.
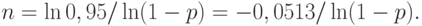
При малом 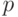 уже не раз применявшееся соотношение из математического анализа дает с достаточной для практики точностью
уже не раз применявшееся соотношение из математического анализа дает с достаточной для практики точностью
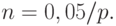
С вероятностью 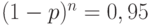 партия принимается, с вероятностью 0,05 подвергается разбраковке. В первом случае партия поступает к потребителю с тем же уровнем дефектности, что и до контроля, но при этом добавляются затраты на контроль, равные
партия принимается, с вероятностью 0,05 подвергается разбраковке. В первом случае партия поступает к потребителю с тем же уровнем дефектности, что и до контроля, но при этом добавляются затраты на контроль, равные 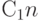 . Партию необходимо пополнить
. Партию необходимо пополнить 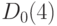 изделиями (затраты
изделиями (затраты 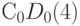 ), общие затраты (в среднем на одну выпущенную партию) равны
), общие затраты (в среднем на одну выпущенную партию) равны 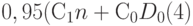 ).
).
Во втором случае фактически проводится сплошной контроль с исправлением дефектов и затратами 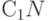 . Суммарные затраты при использовании выборочного контроля равны
. Суммарные затраты при использовании выборочного контроля равны
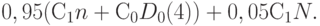
Он более выгоден, чем отсутствие контроля (с добавлением "запасных" изделий), в случае справедливости неравенства

что эквивалентно неравенству
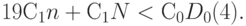
Сравнение с формулой (15) показывает, что если контроль не является разрушающим, то выборочный контроль менее выгоден, чем сплошной (по сравнению с формулой (15) добавляется первое слагаемое в левой части последней формулы), и тем более весьма проигрывает в экономической эффективности по сравнению с отсутствием контроля в сочетании с пополнением партии.
Итак, введение статистического контроля в схеме пополнения партии не выгодно.
От системы контроля к системе технического обслуживания. Вернемся к первому из указанных ранее вариантов замены продукции. Что выгоднее - сплошной контроль на предприятии или замена дефектных изделий, обнаруженных потребителями? Реальное перекладывание контроля на потребителей влечет потери, связанные с удовлетворением их претензий, но при малой доле дефектных изделий эти потери малы по сравнению с затратами на контроль.
Действительно, пусть 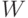 - средние потери поставщика, связанные с пропуском потребителю дефектной единицы продукции. Сюда входят, в частности, такие виды потерь:
- средние потери поставщика, связанные с пропуском потребителю дефектной единицы продукции. Сюда входят, в частности, такие виды потерь:
- стоимость новой единицы продукции (при замене изделия или возврате его стоимости);
- расходы системы распределения продукции и гарантийного ремонта, включая издержки на устранение дефектов;
- потери из-за нежелательного изменения предпочтений потребителя, из-за снижения имиджа фирмы;
- затраты на возмещение ущерба, понесенного потребителем, страховые сборы, судебные издержки, и т.д.
Потери 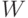 в несколько раз (по экспертной оценке - обычно в 5-10 раз) превышают расходы
в несколько раз (по экспертной оценке - обычно в 5-10 раз) превышают расходы  на изготовление единицы продукции. Кроме того, для быстрого решения проблем потребителей, связанных с обнаружением дефектов, необходима развитая система технического обслуживания.
на изготовление единицы продукции. Кроме того, для быстрого решения проблем потребителей, связанных с обнаружением дефектов, необходима развитая система технического обслуживания.
Пусть изготовлена партия продукции объема  . Тогда расходы на сплошной (неразрушающий) контроль составляют
. Тогда расходы на сплошной (неразрушающий) контроль составляют 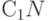 (при этом дефектные единицы продукции извлекаются и утилизируются, расходами на утилизацию или доходами от нее в настоящем изложении пренебрегаем). Пусть
(при этом дефектные единицы продукции извлекаются и утилизируются, расходами на утилизацию или доходами от нее в настоящем изложении пренебрегаем). Пусть 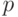 - доля дефектных единиц продукции в партии. Тогда
- доля дефектных единиц продукции в партии. Тогда  - математическое ожидание числа дефектных единиц продукции в партии, а
- математическое ожидание числа дефектных единиц продукции в партии, а 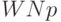 - математическое ожидание потерь. Если
- математическое ожидание потерь. Если
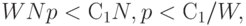 |
( 17) |
то выгоднее отказаться от сплошного контроля. При повышении качества, т.е. снижении доли дефектности, целесообразно переходить к поиску и устранению дефектов не непосредственно на предприятии, а в пунктах системы технического обслуживания.
В формуле (17) участвует математическое ожидание 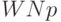 . Реальные потери могут быть больше, но не намного. Как и выше, с помощью теоремы Муавра-Лапласа можно утверждать, что практически наверняка они не превышают
. Реальные потери могут быть больше, но не намного. Как и выше, с помощью теоремы Муавра-Лапласа можно утверждать, что практически наверняка они не превышают 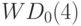 , а потому преимущество решения об отказе от контроля неоспоримо при
, а потому преимущество решения об отказе от контроля неоспоримо при
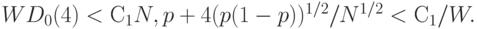 |
( 18) |
Аналогично выводу неравенства (16) заключаем, что неравенство (18) наверняка будет выполнено, если
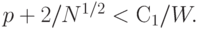 |
( 19) |
Пусть 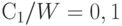 , выпускается партия объема
, выпускается партия объема 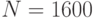 . Тогда согласно неравенству (19) отказ от контроля выгоден уже при
. Тогда согласно неравенству (19) отказ от контроля выгоден уже при 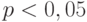 , т.е. граничное значение соответствует довольно низкому уровню качества - 1 единица продукции из 20.
, т.е. граничное значение соответствует довольно низкому уровню качества - 1 единица продукции из 20.
Выгодно ли в рассматриваемой ситуации вводить выборочный контроль? Пусть объем контроля равен n, приемочное число 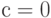 , с вероятностью y партия принимается, а с вероятностью
, с вероятностью y партия принимается, а с вероятностью 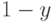 бракуется (и затем подвергается разбраковке). В первом случае расходы на контроль равны
бракуется (и затем подвергается разбраковке). В первом случае расходы на контроль равны 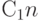 , а остальная часть партии содержит в среднем
, а остальная часть партии содержит в среднем 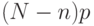 дефектных единиц продукции, и средние издержки равны
дефектных единиц продукции, и средние издержки равны  . Во втором случае суммарные затраты равны
. Во втором случае суммарные затраты равны  Следовательно, введение контроля выгодно, если
Следовательно, введение контроля выгодно, если

Преобразуем это неравенство к виду
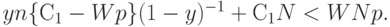 |
( 20) |
Если выполнено неравенство 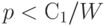 , то второе слагаемое в левой части неравенства (20) больше правой части этого неравенства, в то время как первое слагаемое в левой части (20) положительно. Следовательно, неравенство (20) неверно, и введение выборочного контроля нецелесообразно - как и в разобранном ранее случае метода пополнения партий.
, то второе слагаемое в левой части неравенства (20) больше правой части этого неравенства, в то время как первое слагаемое в левой части (20) положительно. Следовательно, неравенство (20) неверно, и введение выборочного контроля нецелесообразно - как и в разобранном ранее случае метода пополнения партий.
Выше приведен базовый (простейший, исходный) метод сравнения различных систем взаимоотношений поставщиков и потребителей. При разработке практически пригодных систем принятия решений целесообразно дальнейшее его развитие.
Отметим в заключение, что реально статистический контроль качества продукции, осуществляемый поставщиком (выходной контроль), решает две основные задачи: обеспечение интересов потребителя и обнаружение разладок собственных технологических процессов (по результатам контроля последовательности партий). Как показано выше, для решения первой из этих задач он не всегда оптимален. Вторую из названных задач также часто эффективнее решать с помощью иных методов, например, обнаруживать разладку технологических процессов с помощью тех или иных контрольных карт. Таким образом, область применения методов статистического приемочного контроля является довольно ограниченной. Очевидно, однако, что нельзя исключать эти методы из арсенала менеджеров по качеству, в частности, при использовании концепции "всеобщего управления качеством (TQM - Total Quality Management)". Хотя бы потому, что они незаменимы при использовании разрушающих методов контроля.
Наиболее перспективным представляется использование полученных результатов в рамках концепции контроллинга , точнее, в рамках такой научно-практической дисциплины, как контроллинг качества.
Итак, мы рассмотрели основной парадокс теории статистического приемочного контроля - повышение качества выпускаемой продукции приводит к увеличению объема контроля. Описан способ разрешения этого парадокса - на основе перехода от чисто технической политики выбора плана контроля к технико-экономической. Она исходит из сравнения по экономическим показателям схем контроля и схем технического обслуживания и пополнения партий. Проанализирован базовый метод такого сравнения, позволяющий выделить область экономического преимущества схемы пополнения партий и схемы технического обслуживания по сравнению со схемой контроля.
