НОУ ИНТУИТ | Теория и методы разработки управленческих решений. Лекция 12: Моделирование в теории принятия решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 11.08.2009 | Доступ: свободный | Студентов: 5613 / 1112 | Оценка: 4.45 / 4.23 | Длительность: 28:40:00

Темы: Экономика, Менеджмент

Специальности: Руководитель

|

Вам нравится? Нравится 119 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример процесса подготовки решений на основе демографических моделей

Для подготовки и принятия решений в государственном и муниципальном управлении, в маркетинге, в стратегическом менеджменте и в других областях организационно-экономической деятельности необходимы прогнозы численности населения, его полового и возрастного состава.

Используют ряд подходов к прогнозированию демографических характеристик. Можно взять временной ряд численности населения и прогнозировать его с помощью того или иного статистического или экспертного метода. При этом формирование модели формирования населения не предполагается. Несмотря на это, из-за большой инерционности демографических процессов такое "внешнее" прогнозирование оказывается полезным, особенно на небольших интервалах прогноза.

"Внешнее" прогнозирование не всегда позволяет разобраться в существе процесса. Рассмотрим, например, такой показатель, как смертность (число умерших на 1000 человек). Смертность зависит не только от здоровья населения, но и от его полового и возрастного состава. Например, в "молодом" обществе, в котором много детей, а потому его численность растет, смертность будет маленькой, хотя старшее поколение может умирать сравнительно рано, в 40-50 лет. Наоборот, в стабилизировавшемся по численности или вырождающемся обществе, в котором много пожилых людей и мало молодежи, смертность будет велика, даже если продолжительность жизни достигает 80-100 лет.

Рост смертности может быть вызван двумя основными причинами - ухудшением социально-экономического положения населения и изменением половой и возрастной структуры населения. Однако если наблюдается резкий рост (или снижение) смертности, то это - результат действия первой причины, поскольку структура населения меняется медленно. Например, можно констатировать, что в СССР в результате антиалкогольной компании середины 1980-х годов смертность заметно снизилась (относительно прогнозируемой на основе зависимости, полученной по предыдущим годам). А в 1990-х годах в России и других республиках бывшего СССР резко повысилась, особенно в начале десятилетия, из-за снижения в разы жизненного уровня населения и тяжелой социально-экономической обстановки.

С рождаемостью ситуация сложнее, поскольку на нее влияют не только перечисленные причины, но и изменение стиля жизни. Если сто и более лет назад интересы большинства женщин были ориентированы на семью с большим числом детей (многие из которых умирали в младенчестве), то в течение ХХ в. значительная часть женской половины человечества стала заниматься профессиями, которые прежде были чисто мужскими. Перед такими "мигрантами" возник выбор - рождение детей или профессиональное продвижение. В результате появилось понятие "планирование семьи", а рождаемость сократилась.

Правительства различных стран успешно занимались управлением рождаемостью. Для одних стран, таких, как Китай, Индия, целью было сокращение рождаемости. В странах с сильной государственной властью эффективными оказались административные методы. Например, в Китае в городах долгое время городской семье разрешалось иметь только одного ребенка. За рождением второго следовали санкции - штрафы, повышенная оплата за детские товары, медицинское обслуживание, обучение. Поскольку в европейских странах, таких, как Франция и Германия, падение рождаемости во второй половине ХХ в. угрожало депопуляцией, то для стимулирования рождаемости применялись различные экономические меры, в частности, выплата значительных пособий на воспитание детей. Во Франции пособия на трех детей превышали среднюю заработную плату по стране. В результате снижение численности коренного населения удалось на некоторое время предотвратить.

Демографические модели. Для более точного демографического прогнозирования, количественного, а не только качественного, необходимо использовать модели динамики половозрастного состава населения. Такие модели основываются на прослеживании судьбы поколения, рожденного в определенный временной промежуток, например, в год 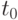t_0 . Пусть всего в этот год родилось 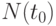N(t_0) человек. Далее каждый год их количество будет уменьшаться, пока не достигнет 0.

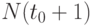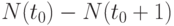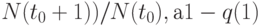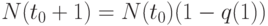Через год численность поколения составит N(t_0+1) человек. За год умерли N(t_0) - N(t_0+1) человек. Частота смерти за первый год составляет q(1) = (N(t_0) - N(t_0+1))/N(t_0), а 1- q(1) - частота того, что человек благополучно перейдет в следующую возрастную категорию. Ясно, что N(t_0+1)= N(t_0)(1- q(1)) .

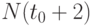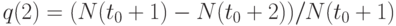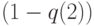Через два года численность поколения составит N(t_0+2) человек. За второй год умерли N(t_0+1) - N(t_0+2) человек. Частота смерти за второй год составляет q(2) = (N(t_0+1) - N(t_0+2))/N(t_0+1) . При этом (1- q(2)) - частота того, что человек благополучно перейдет в следующую возрастную категорию. Ясно, что 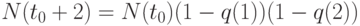N(t_0+2) = N(t_0)(1-q(1))(1- q(2)) . И так далее.

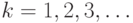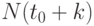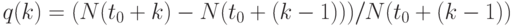Через лет, $k=1,2,3,\dots$ , численность поколения составит N(t_0+ k) человек. За -ый год умерли N(t_0+k) - N(t_0+(k-1)) человек. Частота смерти за второй год составляет q(k) = (N(t_0+k) - N(t_0+(k-1)))/N(t_0+ (k-1)) . Очевидно, 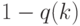1- q(k) - частота того, что человек благополучно перейдет в следующую возрастную категорию. Ясно, что $N(t_0+ k)= N(t_0) (1-q(1))(1- q(2))\dots(1- q(k))$ .

Возрастные коэффициенты смертности. Здесь 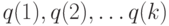$q(1), q(2),\dots q(k)$ ,…- погодовые возрастные коэффициенты смертности. Это - частоты некоторых событий, т.е. оценки соответствующих вероятностей. Но поскольку наблюдений много, можно не делать различия между частотами и вероятностями. Возрастной коэффициент смертности 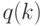q(k) есть условная вероятность того, что человек, проживший (k-1) лет, умрет в течение k-го года. Возрастные коэффициенты смертности рассчитывают не только для всего населения в целом, но отдельно для мужчин и женщин, для различных регионов, социальных групп (например, жителей крупных городов и сельских поселений). Часто используют более длинные промежутки времени, чем год, особенно при выделении поколений. Например, поколением считаются все, родившиеся с 1945 г. по 1954 г. 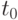Очевидно, возрастные коэффициенты смертности зависят от начала отсчета t_0 - от "даты рождения" поколения. Прослеживают судьбу поколения в течение 90-100 лет, поскольку в настоящее время лишь мизерные доли процента численности поколения живут дольше.

На возрастные коэффициенты смертности конкретных поколений никак не влияет половозрастная структура всего населения. А вот изменение социально-экономического положения и уровня медицинского обслуживания населения, как показывают статистические наблюдения, отражаются в изменении возрастных коэффициентов смертности. Например, в 1999 г. возрастные коэффициенты смертности российских мужчин и женщин выросли (по сравнению с предыдущим годом) примерно на 10% для всех поколений от 20 до 60 лет. Это наглядно говорит об ухудшении социально-экономической обстановки и условий жизни в 1999 г., что можно связать с двукратным падением уровня жизни среднего жителя России в результате экономического кризиса, последовавшего за дефолтом в августе 1998 г.

Погодовые возрастные коэффициенты смертности 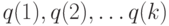$q(1), q(2),\dots q(k)$ ,…позволяют рассчитать различные демографические характеристики поколения. Например, вероятность 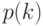p(k) того, что продолжительность жизни представителя поколения составляет ровно лет, равна вероятности того, что он переживет (k-1) контрольных сроков и умрет до наступления -го, т.е. равна

$p(k)=(1-q(1))(1-q(2))\dots(1-q(k-1))q(k)$

Таким образом, продолжительность жизни моделируется дискретной случайной величиной с распределением

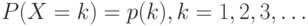
$P(X=k)=p(k), k=1,2,3,\dots$

Средняя продолжительность жизни в рассматриваемом поколении, т.е. математическое ожидание продолжительности жизни, есть

$MX=\sum_{n=1}^{100}kp(k)$

Строго говоря, все эти характеристики можно рассчитать только после того, как поколение закончит свой жизненный путь (по крайней мере, через сто лет после начала отсчета t0). Однако судьба ушедшего поколения волнует немногих. И возрастные коэффициенты смертности используются в демографии по-другому.

Базовая модель в демографии может быть описана так: возрастные коэффициенты смертности постоянны и равны значениям, рассчитанным за последний год. Это значит, что демографическая ситуация в год t описывается вероятностями 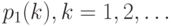$p_1(k), k = 1,2,\dots$ , причем 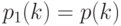p_1(k) = p(k) для поколения, чей жизненный путь начался в году 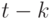t - k . Таким образом, по данным 2004 г. вероятность 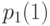p_1(1) рассчитывается для рожденных в 2003 г., 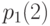p_1(2) - для детей 2002 года рождения, 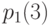p_1(3) - для поколения 2001 г.,…, 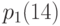p_1(14) - для тех, кто родился в 1990 г., …, 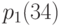p_1(34) - для поколения 1970 г.,…, 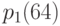p_1(64) - для родившихся в 1940 г.,…, 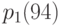p_1(94) - для лиц 1910 г. рождения. Можно сконструировать случайную величину Х_1 - продолжительность жизни в предположении постоянства имеющихся в фиксированный момент временных коэффициентов смертности. Ее распределение имеет вид